沪科版（2024）九年级上册23.2解直角三角形及其应用优秀ppt课件

这是一份沪科版（2024）九年级上册23.2解直角三角形及其应用优秀ppt课件，共24页。PPT课件主要包含了课件说明，什么叫解直角三角形，复习旧知，a2＋b2c2，3边角之间的关系，∠A＋∠B90°，sinA，cosA，tanA，新课讲解等内容，欢迎下载使用。

教学目标： 1．熟练掌握解直角三角形的方法； 2．能将非直角三角形转化为直角三角形有关 的图形计算问题． 教学重点： 灵活运用解直角三角形解决与直角三角形有关的图形计算问题． 教学难点：将非直角三角形转化为直角三角形有关 的图形计算问题．
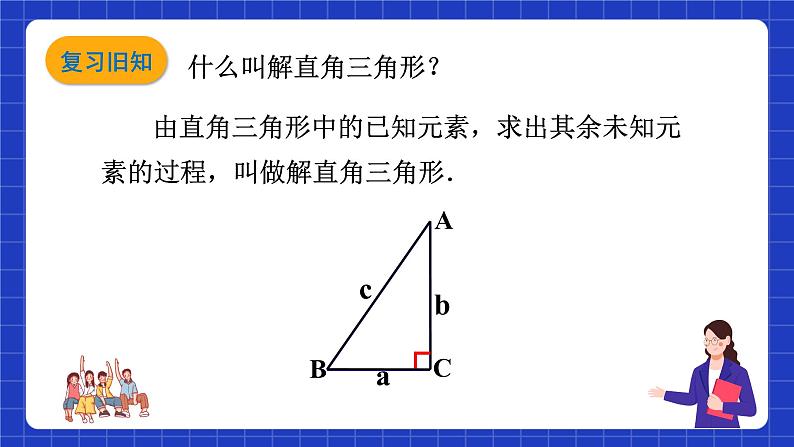
　　 由直角三角形中的已知元素，求出其余未知元素的过程，叫做解直角三角形．
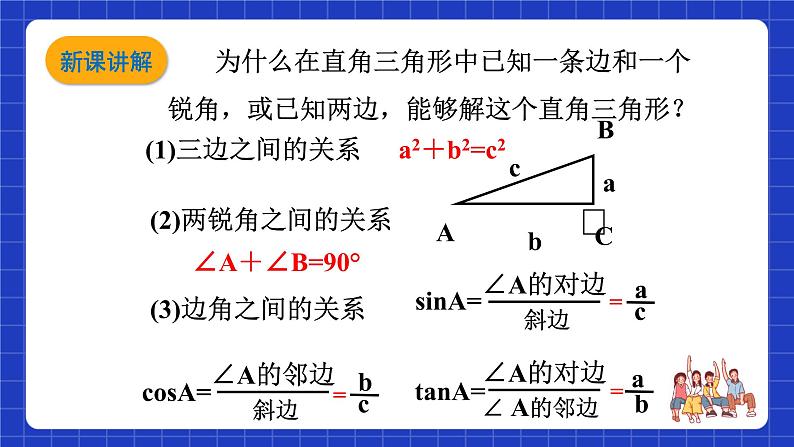
(1)三边之间的关系　　　　　
(2)两锐角之间的关系 　　
　　　为什么在直角三角形中已知一条边和一个锐角，或已知两边，能够解这个直角三角形？
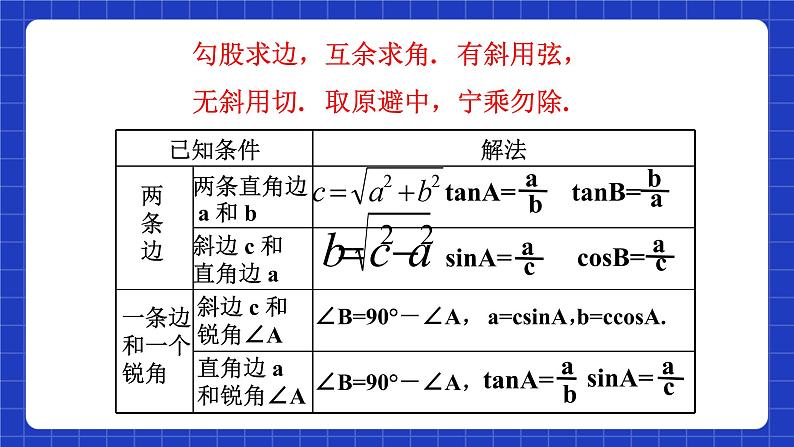
两条直角边 a 和 b　　　　
斜边 c 和直角边 a　　　　
　　根据不同的已知条件，归纳相应的解直角三角形的方法，完成下表填空.　
一条边和一个锐角　　　　　
斜边 c 和锐角∠A　　　　　
直角边 a 和锐角∠A　　　　　
∠B=90°－∠A，　　　　
勾股求边，互余求角. 有斜用弦，无斜用切. 取原避中，宁乘勿除.
∵a= ，c= ，
∴b2=c2－a2=( )2－( )2=3 ，
∴∠B=90°－ ∠A
∴b= a= .
　例2.在△ABC中，∠A=55°，b=20cm，c=30cm，求三角形的面积S△ABC (精确到0.1cm2)．
过点C作CD垂直于AB于D.
用Rt△ACD中∠A的正弦
∵sinA= ，
当∠A=55°， b=20cm，c=30cm时，
×30×20×sin55°
×30×20×0.8192
≈245.8(cm2)
1.在△ABC中，AB= 12 ，AC=13，cs B= ， 则BC 边长为 ( ). A.7 B.8 C.8或17 D.7或17
　　2.如图，在△ABC 中，∠B=30°，∠C=45°，AC=4，求 AB 和 BC．
解：过点A作AD垂直于BC于D.
∴∠ADB=∠ADC=90°.
∵sin∠C= ，
cs∠C= ，
∴AD=ACsin45°= ，
CD=ACcs45°= ，
∴AB=2AD= .
∵cs∠B= ，
∴BD=ABcs30°= ，
= ＋
3.在四边形ABCD中，AB∥CD，AB=4，CD=8，AD=6，∠D=43°，求四边形的面积.
∴SABCD= S△ABC＋
(4＋8)·6sin43°
过点A作AE垂直于DC于E.
∵sinD= ，
∴AE=6·sin43°.
　4．如图，在△ABC 中，∠ACB=90°，CD=6，∠B=30°，CD⊥AB，垂足为 D，若求 AB 的长．
∴∠CDB=∠CDA=90°，
∵tan∠ACD= ，
tan∠BCD= .
∴AD=CDtan30°= ，
BD=CDtan60°= ，
∴∠B=90°－ ∠A=90°－60°=30°.
∵tanA= ，
∴a=btan60°=
5.在 Rt△ABC 中，∠C=90°，根据下列条件解直角三角形：(3)∠A=60°，△ABC 的面积S=　　 ．
6.如图，在Rt△ABC中，∠C=90° ，AC=8，sinB= ，D为线段BC上一点，并且CD=2.(1)求BD的值；(2)求cs∠DAC的值.
(1)根据锐角三角函数关系得出AB的长， 再利用勾股定理得出BC的长， 从而得出BD的长；
(2)在Rt△ACD中，利用勾股定理得出 AD的长， 再根据锐角三角函数的定义求解.
在Rt△ABC中，sinB= = . ∵AC=8，在Rt△ABC中，由勾股定理，得BC2=AB2－AC2=102－82=36，∵CD=2， (2)在Rt△ACD中，AC=8，CD=2. 由勾股定理，得 AD2=AC2＋ CD2=82＋22=68，
∴AD= .
∴BD=BC－CD=6－2=4.
7.如图，在锐角△ ABC中，AB=10，AC=2 ， sinB= .(1)求tan C；(2)求线段BC的长.
过点A作AD⊥BC于点D，根据已知条件可得出 AD的长，利用勾股定理得出CD的长，进而得出tanC的值；
(2)在Rt△ABD中，利用勾股定理求出BD=8， 结合CD的长，即可求出 BC的长.
在Rt△ABD中，AB=10， ，∴AD=6.在Rt△ACD中，AC= ，AD=6，由勾股定理，得CD=AC2－AD2=( )2 －62=
过点A作AD ⊥ BC 于点D.
(2)在Rt△ABD中，AB=10，AD=6.
∴BC=BD＋CD=8＋4=12.