初中数学沪科版（2024）九年级上册第22章 相似形22.1 比例线段精品ppt课件

这是一份初中数学沪科版（2024）九年级上册第22章 相似形22.1 比例线段精品ppt课件，共27页。PPT课件主要包含了探究新知，观察与思考，相似图形的概念，相同点，形状相同，不同点，大小不相同，全等图形，图形的放大，二相似图形的关系等内容，欢迎下载使用。
如图：四边形A1B1C1D1是四边形ABCD经过相似变换所得的．请分别求出这两个四边形的对应边的长度，并分别量出这两个四边形各个内角的度数，然后与你的同伴议一议：这两个四边形的对应角之间有什么关系？对应边之间有什么关系？
这两个四边形对应角相等，对应边的比相等．
多啦 A 梦的 2 寸照片和 4 寸照片，它的形状改变了吗？大小呢？
一 相似多边形的概念
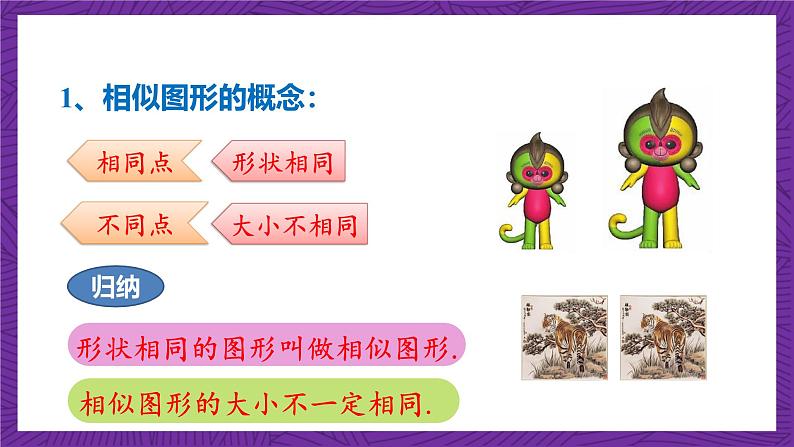
这些图形有什么相同和不同的地方？
形状相同的图形叫做相似图形.
相似图形的大小不一定相同.
形状、大小都相同的图形称为全等图形。
全等图形是相似图形的特殊情况
相似图形与全等形有何区别？
全等形形状相同，大小也相同．
而相似图形形状相同，大小一般不同．
3、图形的相似具有传递性
如果图形A与图形B相似，图形B与图形C相似， 那么图形A与图形C相似。
生活中存在大量相似的图形，试举出几例。
两个图形相似，其中一个图形可以看作由另一个图形放大或缩小得到.
你见过哈哈镜吗？哈哈镜与平面镜中的形象哪一个与你本人相似？
放大镜下的图形和原来的图形相似吗？
放大镜下的角与原图形中角是什么关系?
多边形 ABCDEF 是显示在电脑屏幕上的，而多边形 A1B1C1D1E1F1 是投射到银幕上的.
根据相似多边形的概念，你知道相似多边形的性质吗？
相似多边形的对应角相等，对应边长度的比相等．
三 相似多边形的性质及应用
例1：下图是两个正方形、两个等边三角形．观察图形，回答下列问题．
(1)每组的两个图形的形状相同吗？
(2)每组的两个图形相似吗？
(3)计算每组的两个图形的对应边的长度的比、对应角有什么关系？
(4)你能归纳上面的结论吗？
对应边的长度比相等，对应角相等．
两个边数相同的多边形，如果它们的对应角相等，对应边长度的比相等，那么这两个多边形叫做相似多边形．
相似多边形的对应角相等，对应边成比例.
相似多边形的对应边长度的比叫作相似比或相似系数．
例2 一块长3m，宽1.5m的矩形黑板，镶在其外围的木质边框宽7.5cm，边框的内外边缘所围成的两个矩形相似吗？为什么？
解：矩形黑板的四个内角都是90°，
长为3m＝300cm，宽为1.5m＝150cm，
长为300＋7.5×2＝315(cm)，宽为150＋7.5×2＝165(cm)，
长∶宽＝300∶150＝2∶1，
边框的外缘所围成的四个内角为90°，
长∶宽＝315∶165＝21∶11，又2∶1≠21∶11，
即两矩形的对应边不成比例，所以边框的内外边缘所围成的两个矩形不相似．
例3 如图，把矩形ABCD对折，折痕为MN，矩形DMNC与矩形ABCD相似，已知AB＝4.
解：(1)由对折知AM＝ AD，设DM＝x，AD＝2x.
∵矩形DMNC与矩形ABCD相似，
(2)求矩形DMNC与矩形ABCD的相似比．
DM∶AB＝2 ∶4＝ ∶2.
矩形DMNC与矩形ABCD相似比为
1. 如图所示的两个四边形是否相似？
2．已知线段a、b、c、d成比例， 即 ＝ .其中a＝2cm，b＝3cm，d＝15cm，则c＝______．
3．要做甲乙两个形状相同(相似)的三角形框架，已知三角形框架甲的三边分别为：50cm、60cm、80cm，三角形框架乙的一边长为20cm，那么符合条件的三角形框架乙共有(　　)A．1种　　　B．2种　　　C．3种　　　D．4种
4．如图，有两个形状相同的星星图案，则x的值为 (　　)
A．15B．12C．10D．8
5. 如图，把矩形 ABCD 对折，折痕为 EF，若矩形ABCD 与矩形 EABF 相似，AB = 1．
解：∵ E 是 AD 的中点，
又∵矩形 ABCD 与矩形 EABF相似，AB=1，
(2) 求矩形 ABEF 与矩形 ABCD 的相似比.
解：矩形 ABEF 与矩形 ABCD 的相似比为：
形状相同的图形叫做相似图形
相似图形的大小不一定相同
相似多边形对应边的比叫做相似比
对应角相等，对应边成比例