沪科版（2024）九年级上册22.2 相似三角形的判定精品ppt课件

这是一份沪科版（2024）九年级上册22.2 相似三角形的判定精品ppt课件，共23页。PPT课件主要包含了旧知回顾，探究新知，符号语言，知识归纳，例题与练习，又∵BD＝CE，∵∠BAD20°，∴∠CAE20°，随堂练习，本课小结等内容，欢迎下载使用。
1．简述全等三角形的判定定理“SSS”内容．
2．我们已经学过相似三角形的哪些判定方法？
平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似．
三边对应相等的两个三角形全等．
两边对应成比例且夹角相等，两三角形相似．
两角对应相等，两三角形相似．
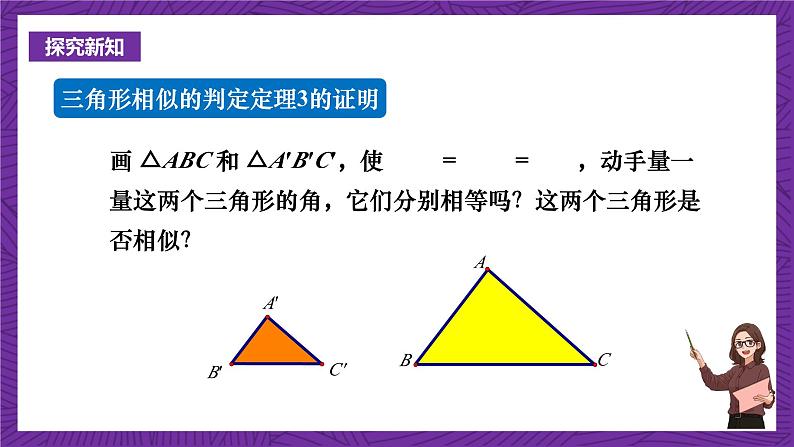
三角形相似的判定定理3的证明
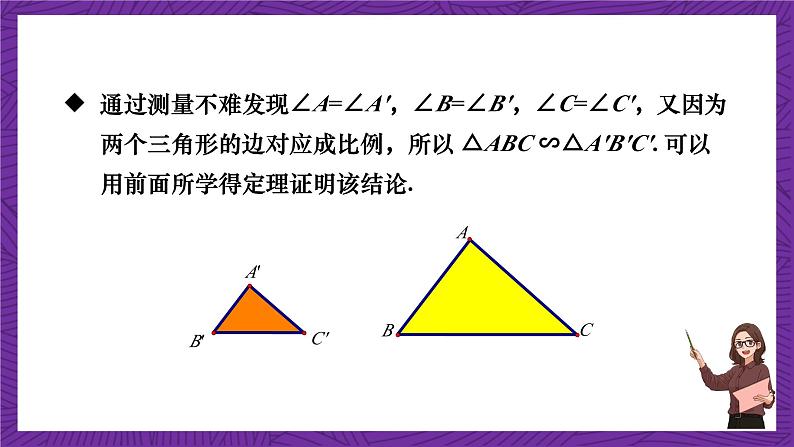
通过测量不难发现∠A=∠A'，∠B=∠B'，∠C=∠C'，又因为两个三角形的边对应成比例，所以 △ABC ∽△A′B′C′. 可以用前面所学得定理证明该结论.
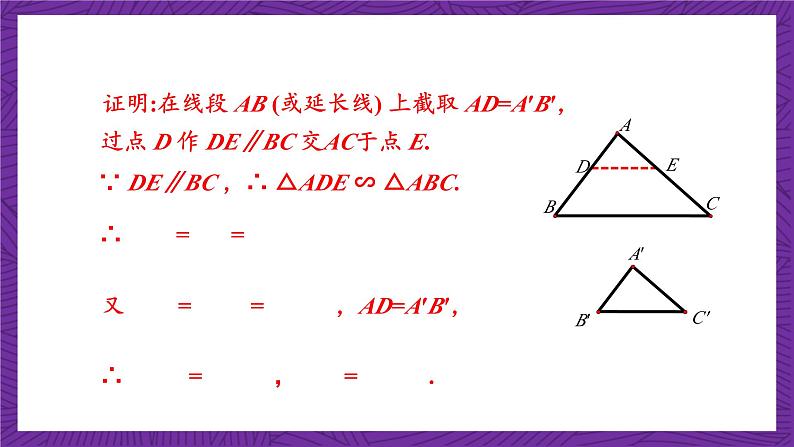
∵ DE∥BC ，∴ △ADE ∽ △ABC.
证明:在线段 AB (或延长线) 上截取 AD=A′B′，
过点 D 作 DE∥BC 交AC于点 E.
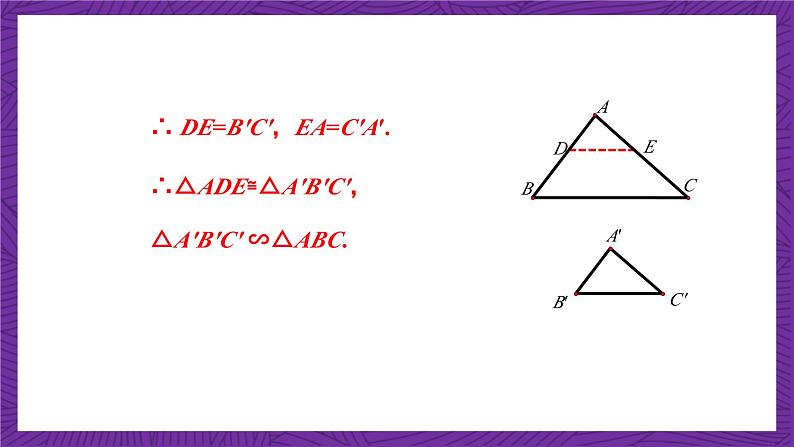
∴ DE=B′C′，EA=C′A′.
∴△ADE≌△A′B′C′，
△A′B′C′ ∽△ABC.
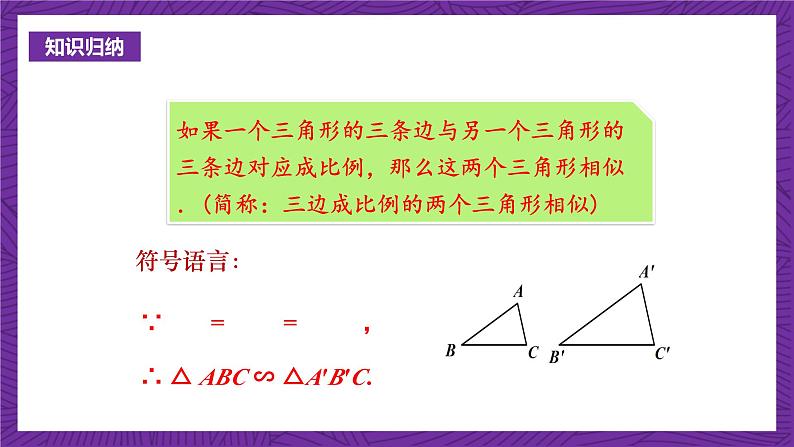
如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似．(简称：三边成比例的两个三角形相似)
∴ △ ABC ∽ △A′B′C.
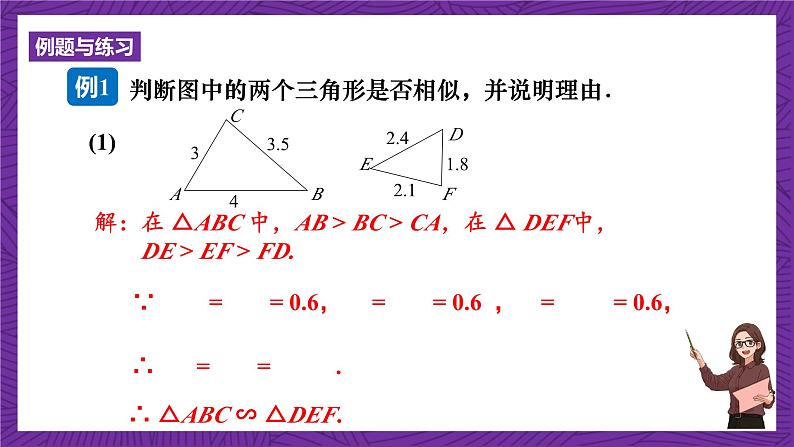
解：在 △ABC 中，AB > BC > CA，在 △ DEF中， DE > EF > FD.
∴ △ABC ∽ △DEF.
∴ △ABC ∽ △A'B'C'.
判定三角形相似的方法之一：如果题中给出了两个三角形的三边的长，分别算出三条对应边的比值，看是否相等.
注意：计算时最长边与最长边对应，最短边与最短边对应.
解：△ ABC与△ A′B′C′的顶点都在格点上，根据勾股定理，得
∴ △ ABC与△ A′B′C′相似.
三角形相似的判定定理3的应用
如图, 方格网的小方格是边长为1的正方形，△ABC与△ A′B′C′的顶点都在格点上，△ ABC与△A′B′C′相似吗?为什么?
【分析】欲证∠BAD＝∠CAE，可先证明△ABC∽△ADE，推出∠BAC＝∠DAE，进而得出结论，而由已知条件中三边对应成比例，知必有两三角形相似．
∴△ABC∽△ADE，
∴∠BAC－∠DAC＝∠DAE－∠DAC，即∠BAD＝∠CAE.
∴∠BAC＝∠DAE，
证明：(1)△ABC是等边三角形，
(1)证明：△ABD≌△BCE；
(2)BD2＝AD·DF吗？为什么？
∴AB＝BC，∠ABD＝∠C＝60°，
∴△ABD≌△BCE(SAS)．
(2)∵△ABD≌△BCE，
∴∠BAD＝∠CBE，
∴BD2＝DF·AD.　
又∵∠ADB＝∠BDF，
∴△ABD∽△BFD，
∴∠BAC=∠DAE，∠BAC －∠DAC = ∠DAE －∠DAC，
∴ △ABC ∽△ADE (三边成 比例的两个三角形相似).
即 ∠BAD=∠CAE.
1.已知ABC的三边长分别为6cm，7.5cm，9cm，△DEF的一边长为4cm，当△DEF的另两边长是下列哪一组时，这两个三角形相似(　　)
A．2cm，3cm　　　B．4cm，5cm　　　C．5cm，6cm　　　D．6cm，7cm
2．如图，在▱ABCD中，AB＝10，AD＝6，E是AD的中点，在边AB上取点F，当BF＝_______时，△CBF与△CDE相似．
3．如图，小正方形的边长均为1，则图中三角形(阴影部分)与△ABC相似的是(　　)
4．如图，等腰直角三角形ABC中，顶点为C，∠MCN＝45°，试说明△BCM∽△ANC.
解：∵∠A＝∠B＝45°，
又∵∠ANC＝∠NCB＋45°，
∠BCM＝∠NCB＋45°，
∴∠ANC＝∠BCM，
∴△BCM∽△ANC.
5．已知，如图，D为△ABC内一点，连接BD、AD，以BC为边在△ABC外作∠CBE＝∠ABD，∠BCE＝∠BAD.求证：△DBE∽△ABC.
证明：∵∠CBE＝∠ABD，∠BCE＝∠BAD，
∴△ABD∽△CBE，
∵∠ABD＋∠DBC＝∠CBE＋∠DBC，
即∠ABC＝∠DBE，
∴△ABC∽△DBE.
6. 如图，△ABC中，点 D，E，F 分别是 AB，BC，CA的中点，求证：△ABC∽△EFD．
∴ △ABC∽△EFD.
证明：∵△ABC中，点D，E，F分别是AB，BC，CA的中点，
利用三边判定两个三角形相似
三边成比例的两个三角形相似
相似三角形的判定定理的运用