初中数学沪科版（2024）八年级上册12.2 一次函数优质课ppt课件

这是一份初中数学沪科版（2024）八年级上册12.2 一次函数优质课ppt课件，共14页。PPT课件主要包含了谈谈你在本节课的收获，从数到形，从形到数，数学的基本思想方法，数形结合等内容，欢迎下载使用。

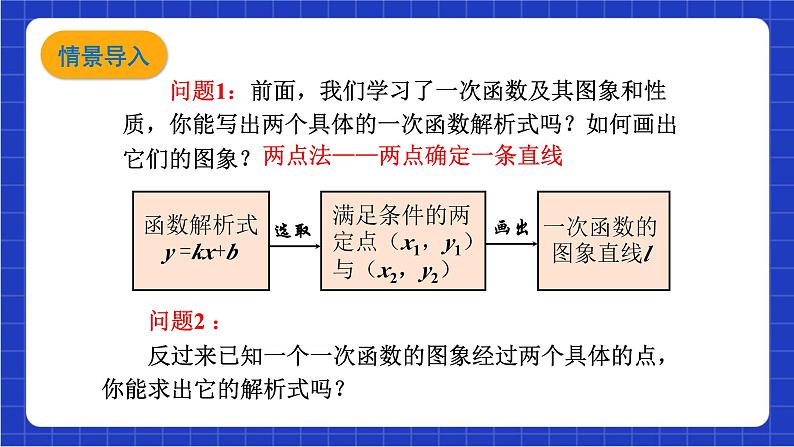
　　问题1：前面，我们学习了一次函数及其图象和性质，你能写出两个具体的一次函数解析式吗？如何画出 它们的图象？
　　问题2 ：　　反过来已知一个一次函数的图象经过两个具体的点，你能求出它的解析式吗？
两点法——两点确定一条直线
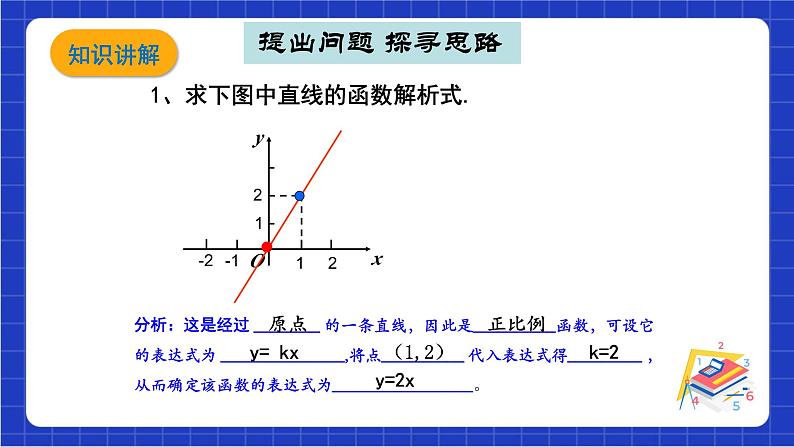
1、求下图中直线的函数解析式.
分析：这是经过 ________ 的一条直线，因此是__________函数，可设它的表达式为 _______________,将点__________ 代入表达式得_________ ，从而确定该函数的表达式为_________________。
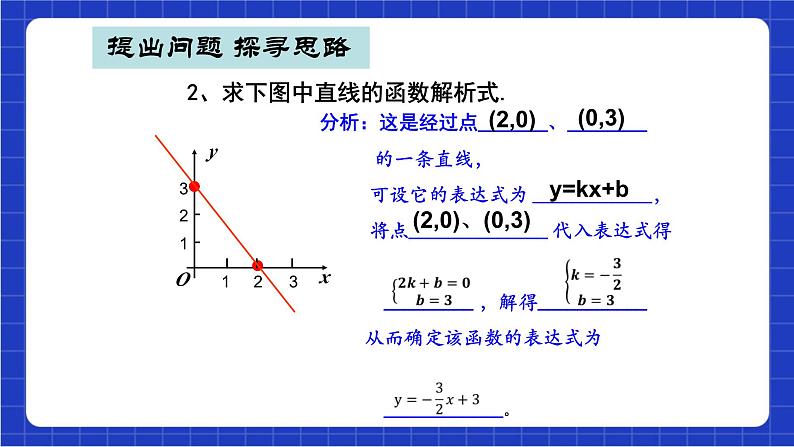
2、求下图中直线的函数解析式.
分析：这是经过点_______、________ 的一条直线， 可设它的表达式为 ____________， 将点______________ 代入表达式得 _________ ，解得___________ 从而确定该函数的表达式为 ____________。
(2,0)、(0,3)
反思：确定正比例函数和一次函数解析式各需几个条件？
确定正比例函数的解析式需要一个条件，确定一次函数的解析式需要两个条件.
例题：已知一次函数的图象过点（4,5）（5,2）. 求这个一次函数的解析式．
解：设这个一次函数的解析式为y=kx+b.
∴这个一次函数的解析式为y= -3x+17
因为图象过（4，5）与（5，2）点，所以这两点的坐标必适合解析式
∵过点（4,5）（5,2）
例题：已知一次函数的图象经过点(4,5)与（5，2）.求这个一次函数的解析式．
象这样先设出函数解析式，再根据条件确定解析式中未知的系数，从而具体写出这个式子的方法，叫做待定系数法.
你能归纳出待定系数法求函数解析式的基本步骤吗？
　　变式1、已知 y是 x的一次函数，当 x=-1时 y=3， 当 x =2 时 y=-3，求 y关于 x 的一次函数解析式．
变式2、若y与x-2成正比例关系，且x=4时y=5，求 y关于x的函数关系．
变式3、已知直线 ，与直线 平行，且过点（4,6）.求解析式．
变式4：如图，大拇指与小拇指尽量张开时，两指间的距离称为指距.某项研究表明，一般情况下人的身高h是指距d 的一次函数.下表是测得的指距与身高的一组数据：
（1）求出h与d之间的函数解析式.
（2）某人身高为196 cm，一般情况下他的指距应是多少？
解：（1）设 h=kd+b． 把d=20，h=160；d=21，h=169， 分别代入上式得， 20k+b＝160， 21k+b＝169. 解得 k=9， b=-20， ∴ h=9d-20. （2）当h=196时，196=9d-20，解得d=24（cm）．
函数解析式y=kx+b