初中数学沪科版（2024）八年级上册13.2 命题与证明优质ppt课件

这是一份初中数学沪科版（2024）八年级上册13.2 命题与证明优质ppt课件，文件包含沪科版数学八上132《命题与证明》第3课时课件pptx、沪科版数学八上132《命题与证明》第3课时教案docx等2份课件配套教学资源，其中PPT共22页， 欢迎下载使用。
1.了解辅助线的概念，理解辅助线在解题过程中的用处.2.掌握“三角形内角和定理”的证明及其简单应用.3.理解和掌握三角形内角和定理的推论1和推论2.4.经历三角形内角和定理的推理证明过程，培养学生勇于探索、合作交流的精神，培养学习数学的兴趣，感悟逻辑推理的数学价值.
回顾一：回想一下证明的一般步骤是什么？
①理解题意：分清命题的条件(已知)、结论(求证)；
②根据前边的分析，写出已知、求证，并画出图；
③分析因果关系，找出证明途径；
④有条理地写出证明过程.
三角形的内角和等于180°.
回顾二：三角形的内角和定理是什么？
追问：我们当时是怎样验证的？
测量法、拼剪法、折叠法.
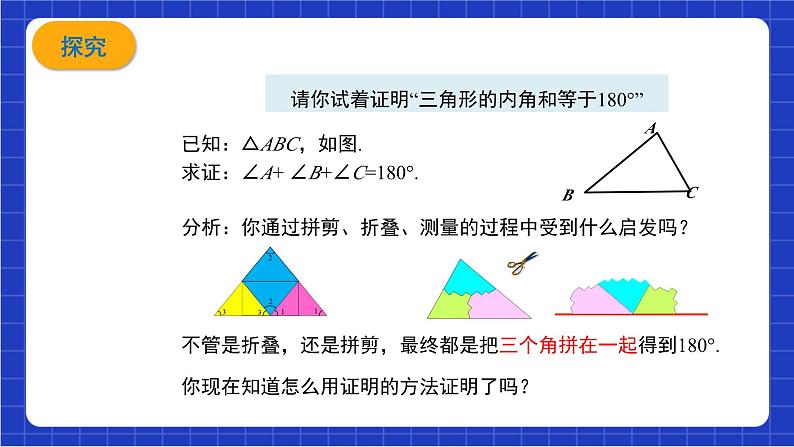
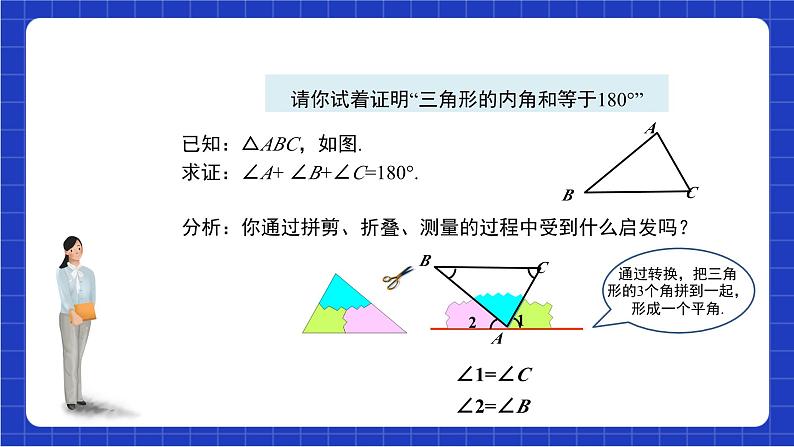
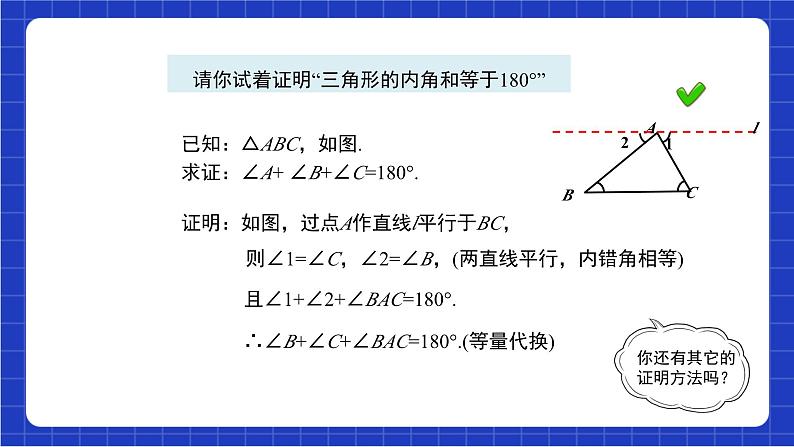
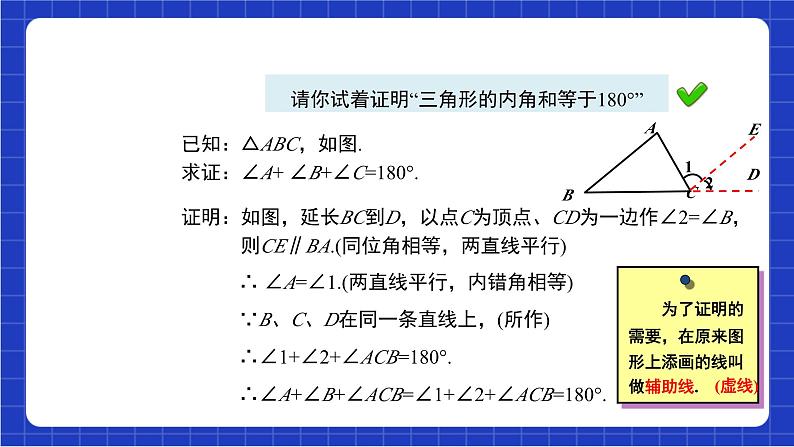
请你试着证明“三角形的内角和等于180°”
已知：△ABC，如图.求证：∠A+ ∠B+∠C=180°.
分析：你通过拼剪、折叠、测量的过程中受到什么启发吗？
不管是折叠，还是拼剪，最终都是把三个角拼在一起得到180°.
你现在知道怎么用证明的方法证明了吗？
证明：如图，过点A作直线l平行于BC， 则∠1=∠C，∠2=∠B，(两直线平行，内错角相等)
且∠1+∠2+∠BAC=180°.
∴∠B+∠C+∠BAC=180°.(等量代换)
证明：如图，延长BC到D，以点C为顶点、CD为一边作∠2=∠B， 则CE∥BA.(同位角相等，两直线平行)
∴ ∠A=∠1.(两直线平行，内错角相等)
∵B、C、D在同一条直线上，(所作)
∴∠1+∠2+∠ACB=180°.
∴∠A+∠B+∠ACB=∠1+∠2+∠ACB=180°.
★问题一：在△ABC中，∠C=90°，求：∠A+∠B的度数. 由此你能得到什么结论？
直角三角形的两个锐角的和是90°.
解：在△ABC中， 根据三角形内角和定理，易得∠A+∠B +∠C=180°， 又∠C=90°， ∴ ∠A+∠B=180°–∠C=180°–90°=90°.
直角三角形的两锐角互余.
★问题二：在△ABC中，∠A+∠B=90°，求：∠C的度数. 由此你能得到什么结论？
解：在△ABC中， 根据三角形内角和定理，易得∠A+∠B +∠C=180°， 又∠A+∠B=90°， ∴ ∠C =180°–(∠A+∠B)=180°–90°=90°.
推论 2：有两个角互余的三角形是直角三角形.
在△ABC中，(1)∠C=90°，∠A=30°，则∠B= ；(2)∠A=50°，∠B=∠C，则∠B= ；(3)∠A–∠C=25°，∠B–∠A=10°，则∠B= ；(4)∠A+∠B=90°，则△ABC是 三角形.
例1 如图，在△ABC中，D在BC的延长线上，过D作DE⊥AB于E，交AC于F.已知∠A＝30°，∠FCD＝80°，求∠D.
分析：要计算的是∠D的大小，只要知道它所在三角形中的其它两个角的和即可.已知：① DE⊥AB，即∠DEB=∠FEA＝90°；②∠A＝30°；③ ∠FCD＝80°.
解：∵DE⊥AB，∴∠FEA＝90°.在△AEF中，∵∠FEA＝90°，∠A＝30°，∴∠AFE＝180°–∠FEA–∠A＝60°.又∵∠CFD＝∠AFE， ∴∠CFD＝60°.在△CDF中，∵∠CFD＝60°，∠FCD＝80°，∴∠D＝180°–∠CFD–∠FCD＝40°.
例2 如图，在△ABC中， ∠BAC=40°，∠B=75°，AD是△ABC的角平分线，求∠ADB的度数．
分析：要计算的是∠ADB的大小，只要知道它所在三角形中的其它两个角的和即可.已知：①∠BAC＝40°；②∠B＝75°；③由“AD是△ABC的角平分线”，易得∠CAD=∠BAD.
解：∵AD是△ABC的角平分线，∠BAC=40 °，
在△ABD中，∠ADB=180°–∠B–∠BAD=180°–75°–20°=85°.
【变式题】如图，CD是∠ACB的平分线，DE∥BC，∠A＝50°，∠B＝70°，求∠EDC，∠BDC的度数．
由三角形的内角和定理易得∠A+∠B=∠C+∠D.
由三角形的内角和定理易得∠1+∠2=∠3+∠4.
1.补充完整下列证明，并填上推理的依据：已知：如图，△ABC.求证：∠A+∠B+∠C=180°.证明：过点A作DE∥BC，则 ∠DAB= ，( ) ∠EAC= ，( )∵ ∠DAB+∠BAC+∠EAC= ，(所作)∴ ∠B+ ∠BAC+∠C= + + ( ) =180°.( )
两直线平行，内错角相等
2.补充完成下列证明：已知：如图，△ABC.求证：∠A+∠B+∠C=180°.证明：D是BC边上一点，过点D作DE∥AB，DF∥AC，分别交AC，AB于点E，F. ∵DE∥AB，(所作)
∴∠B=∠3.(两直线平行，同位角相等)∵DF∥AC，(所作)∴∠C=∠1.(两直线平行，同位角相等)
又 ∵∠1+∠2+∠3=180°， ∴∠A+∠B+∠C=180°.(等量代换)
三角形内角和定理的证明
有两个角互余的三角形是直角三角形.
教科书第84页习题13.2第5题