沪科版（2024）八年级上册14.2 三角形全等的判定精品ppt课件

这是一份沪科版（2024）八年级上册14.2 三角形全等的判定精品ppt课件，共16页。PPT课件主要包含了学习目标，想一想，新课导入，“两角及其夹边”，知识讲解，几何语言，随堂训练，课堂小结等内容，欢迎下载使用。
通过画、量、观察、比较和猜想等过程，探索、归纳、证明两个三角形全等的条件——ASA. 掌握用ASA证明两个三角形全等的方法（重点、难点）．能根据所给条件灵活地选择三角形全等的判定方法，并能综合运用全等三角形的性质证明线段和角相等．
如图所示，某同学把一块三角形的玻璃不小心打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是带哪块去？你能说明其中的道理吗？（学生先独立思考，然后再与同学进行交流）
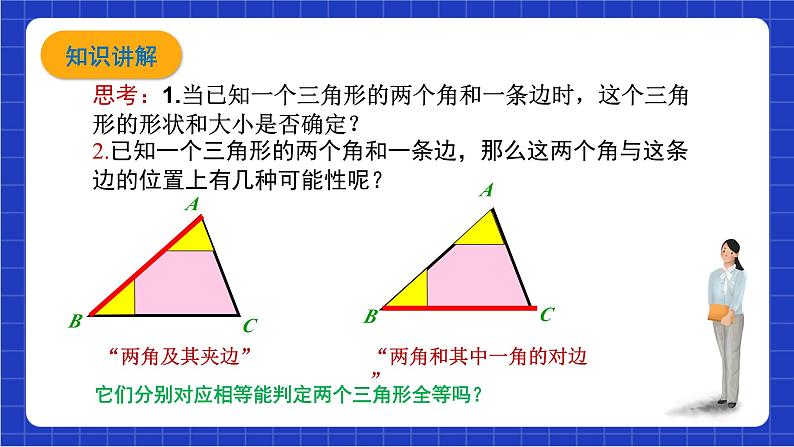
思考：1.当已知一个三角形的两个角和一条边时，这个三角形的形状和大小是否确定？2.已知一个三角形的两个角和一条边，那么这两个角与这条边的位置上有几种可能性呢？
“两角和其中一角的对边”
它们分别对应相等能判定两个三角形全等吗？
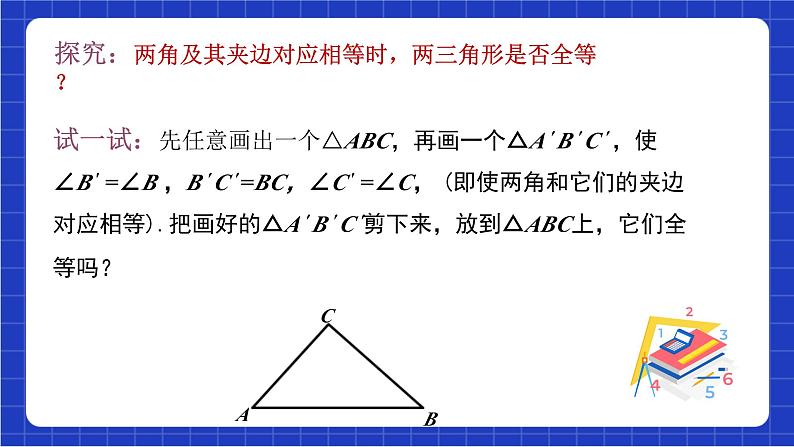
试一试：先任意画出一个△ABC，再画一个△A ′ B ′ C ′ ，使∠B ′ =∠B ，B ′ C ′ =BC，∠C ′ =∠C， (即使两角和它们的夹边对应相等).把画好的△A ′ B ′ C ′剪下来，放到△ABC上，它们全等吗？
探究：两角及其夹边对应相等时，两三角形是否全等？
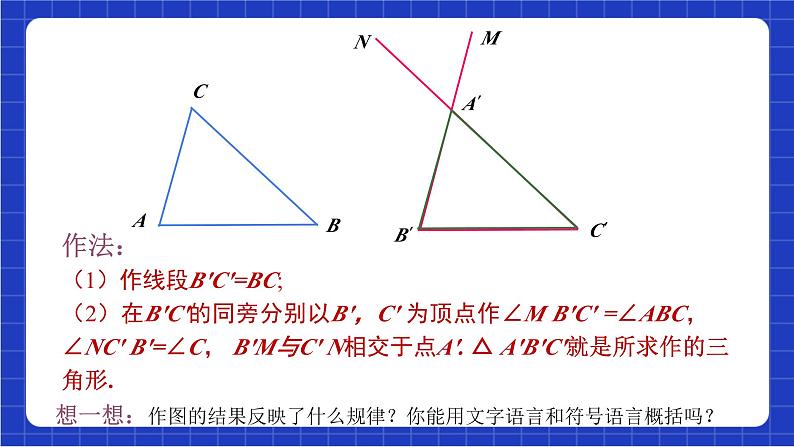
作法：（1）作线段B'C'=BC;（2）在B'C'的同旁分别以B'，C' 为顶点作∠M B'C' =∠ABC， ∠NC' B'=∠C， B'M与C' N相交于点A'. △ A'B'C'就是所求作的三角形.
想一想：作图的结果反映了什么规律？你能用文字语言和符号语言概括吗？
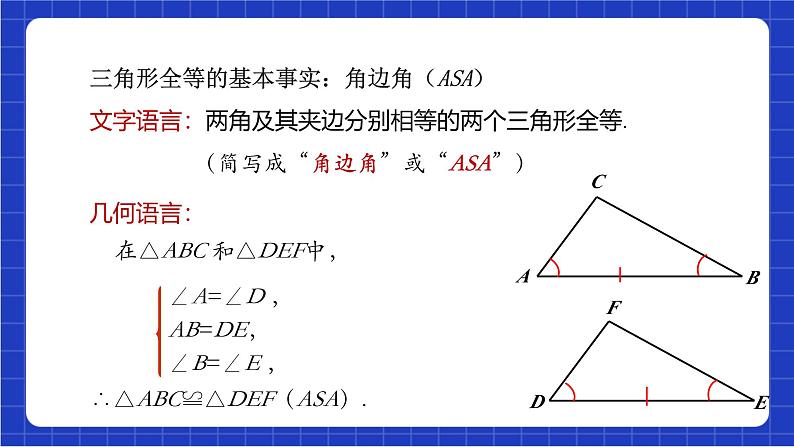
文字语言：两角及其夹边分别相等的两个三角形全等. （简写成“角边角”或“ASA”）
在△ABC 和△DEF中，
∴△ABC≌△DEF（ASA）.
三角形全等的基本事实：角边角（ASA）
∠A=∠D ， AB=DE，∠B=∠E ，
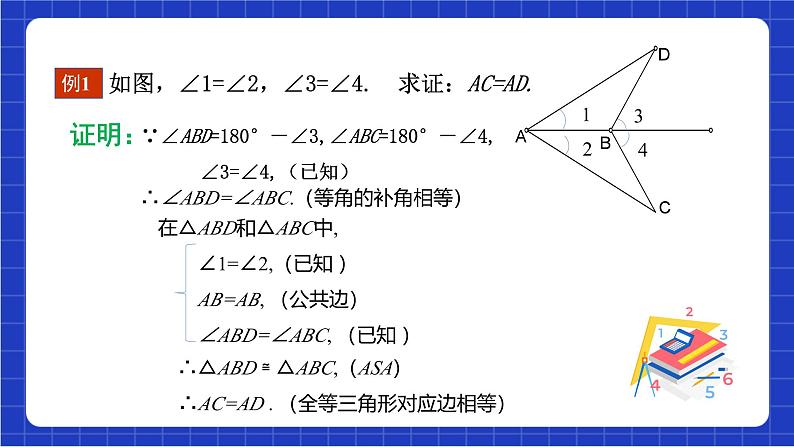
如图，∠1=∠2，∠3=∠4. 求证：AC=AD.
∵∠ABD=180°－∠3,∠ABC=180°－∠4,　　　∠3=∠4,（已知）
∴∠ABD=∠ABC.（等角的补角相等）
在△ABD和△ABC中,　　∠1=∠2,（已知 ）　　AB=AB, （公共边） 　　∠ABD=∠ABC, （已知 ）
∴△ABD ≌ △ABC,（ASA）
∴AC=AD . （全等三角形对应边相等）
证明： ∵AB⊥BD,ED⊥BD,(已知)∴∠ABC=∠EDC=90°(垂直的定义)在△ABC和△EDC中,∵ ∠ABC=∠EDC，（已知） BC=CD，（已知） ∠ACB=∠ECD，（对顶角相等）∴△ABC≌△EDC.(ASA)∴AB=DE.(全等三角形的对应边相等)
已知如图,要测量河两岸相对的两点A,B之间的距离,可以在AB的垂线BF上取两点C,D(BF在河岸上),使BC=CD,再过点D作BF的垂线DE,使点A,C，E在一条直线上,这时测得DE的长等于AB的长,请说明道理.
∴△ACD≌△ABE,（ASA）
已知：点D在AB上，点E 在AC上，BE 和 CD 相交于 点O，AB=AC，∠B=∠C. 求证：BD=CE .
∠A=∠A,（公共角）AC=AB,（已知）∠C=∠B,（已知）
∴AD=AE.（全等三角形的对应边相等）
又∵AB=AC,（已知） ∴BD=CE.
1.已知：如图，AB=A′ C ，∠A=∠A′，∠B=∠C. 求证：△ABE≌ △ A′ CD .
∠A=∠A ′ 已知AB=A ′ C 已知∠B=∠C 已知
ABE A ′ CD(ASA)
△ABE △A ′ CD
2. 在△ABC与△A′B′C′中，已知∠A＝44°，∠B＝67°，∠C′＝69° ，∠A′＝44°，且AC＝A′C′，那么这两个三角形（　 ）A．一定不全等　 B．一定全等　 　C．不一定全等　　 D．以上都不对
3.如图：已知AB∥DE，AC∥DF，BE=CF. 求证：△ABC≌△DEF.
∵ AB∥DE，AC∥DF,（已知 ）
∴ ∠B＝∠DEF ，
∠ACE＝∠F ，（两直线平行，同位角相等）
∵BE=CF,（已知）∴BE+EC=CF+EC,即BC=EF.
∴ △ABC≌△DEF.（ASA）
4.如图，AB∥CD，AD∥BC，那么AB=CD 吗？为什么？AD与BC 呢？
1. 三角形全等的条件：两角及其夹边分别相等的两个三角形全等. (角边角或ASA)
2.利用全等三角形证明线段或角相等，其思路如下： ⑴观察要证的线段和角在哪两个可能全等三角形之中; ⑵分析要证全等的这两个三角形，已知什么条件，还缺什么条件.