数学沪科版（2024）14.2 三角形全等的判定获奖课件ppt

这是一份数学沪科版（2024）14.2 三角形全等的判定获奖课件ppt，共21页。PPT课件主要包含了学习目标，想一想，新课导入，ASA，SSS，SAS，AAS，做一做，知识讲解，⑷连接A＇B＇等内容，欢迎下载使用。

探索直角三角形全等判定条件，能判定两个直角三角形的全等. 在探索直角三角形全等条件及其运用过程中，能有条理的思考并进行简单的推理.
对于两个直角三角形，除了直角相等的条件，还要满足几个条件，这两个直角三角形就全等了？
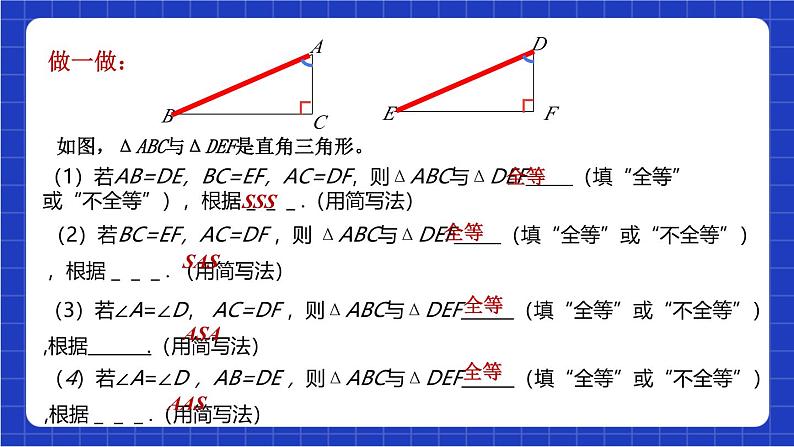
（3）若∠A=∠D， AC=DF ，则ΔABC与ΔDEF （填“全等”或“不全等”）,根据 .（用简写法）
如图，ΔABC与ΔDEF是直角三角形。
（4）若∠A=∠D ，AB=DE ，则ΔABC与ΔDEF （填“全等”或“不全等”）,根据＿＿＿.（用简写法）
（1）若AB=DE，BC=EF，AC=DF，则ΔABC与ΔDEF （填“全等”或“不全等”），根据＿＿＿.（用简写法）
（2）若BC=EF，AC=DF ，则 ΔABC与ΔDEF （填“全等”或“不全等”），根据＿＿＿.（用简写法）
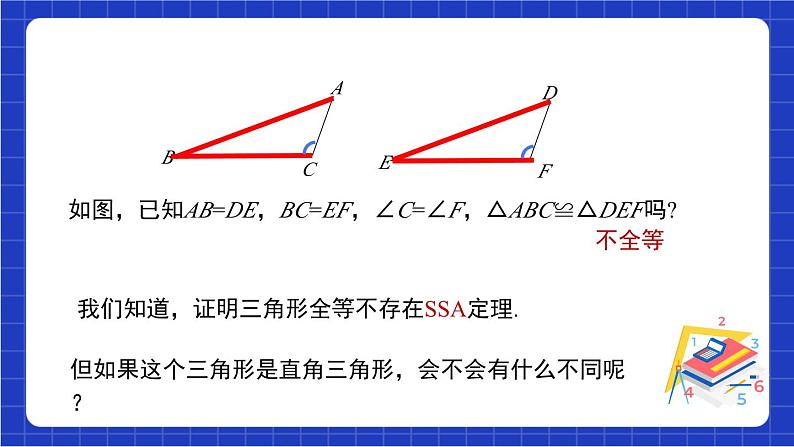
如图，已知AB=DE，BC=EF，∠C=∠F，△ABC≌△DEF吗? 不全等
我们知道，证明三角形全等不存在SSA定理.
但如果这个三角形是直角三角形，会不会有什么不同呢？
探究：直角三角形中，如果满足斜边和一条直角边分别相等，那么这两个直角三角形全等吗？
画一画： 任意画出一个Rt△ABC,使∠C=90°.再画一个Rt△A ′B ′C ′，使∠C′=90 °,A′C′=AC, A ′B ′=AB,把画好的Rt△A′B′ C′ 剪下来，放到Rt△ABC上，它们能重合吗？
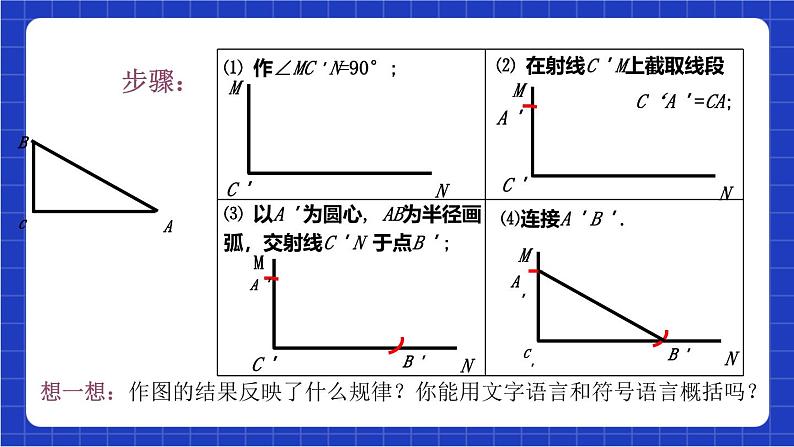
想一想：作图的结果反映了什么规律？你能用文字语言和符号语言概括吗？
⑴ 作∠MC＇N=90°;
⑵ 在射线C＇M上截取线段 C‘A＇=CA;
⑶ 以A＇为圆心, AB为半径画弧，交射线C＇N 于点B＇;
文字语言：斜边和一条直角边分别相等的两个直角三角形全等（简写 成“斜边、直角边”或“HL”）.
在Rt△ABC和Rt △ DEF中，
∴ Rt △ABC ≌ Rt △ DEF（HL）.
直角三角形全等的判定方法：斜边、直角边（HL）
AB=DE，BC=EF (或AC=DF )，
“SSA”可以判定两个直角三角形全等，但是“SS”指的是斜边和一直角边，而“A”指的是直角.
如图，∠BAC=∠CDB=90°， AC﹦BD.求证：AB﹦DC.
∵ ∠BAC=∠CDB=90°
∵ CB=BC, AC=BD ，
在 Rt△ABC 和Rt△BAD 中，
∴ Rt△ABC≌Rt△BAD (HL).
∴ AB﹦DC.(全等三角形的对应边相等)
∴△BAC与△CDB都是直角三角形.
如图，AB =CD, BF⊥AC,DE⊥AC,AE =CF.求证：BF =DE.
在Rt△ABF 和Rt△CDE 中,∵ AE=CF,∴AE+EF=CF+EF,即AF=CE.又∵ AB=CD,∴ Rt△ABF ≌Rt△CDE(HL),∴ BF=DE.
如图，已知AD、AF分别是两个钝角△ABC和△ABE的高，如果AD＝AF，AC＝AE. 求证：BC＝BE.
∵AD、AF分别是两个钝角△ABC和△ABE的高，且AD＝AF，AC＝AE，∴Rt△ADC≌Rt△AFE(HL),∴CD＝EF.∵AD＝AF，AB＝AB，∴Rt△ABD≌Rt△ABF(HL),∴BD＝BF,∴BD－CD＝BF－EF,即BC＝BE.

如图， ∠ACB =∠ADB=90°，要证明△ABC≌ △BAD，还需一个什么条件？把这些条件都写出来，并在相应的括号内填写出判定它们全等的理由. （1） （ ） （2） （ ） （3） （ ） （4） （ ）
∠ DAB= ∠ CBA
∠ DBA= ∠ CAB
已知：如图， △ABC中，AB=AC，AD是高.求证:BD=CD ;∠BAD=∠CAD.
∵AD是高,∴∠ADB=∠ADC=90°.
在Rt△ADB和Rt△ADC中,
∴BD=CD,∠BAD=∠CAD.
∴ Rt△ADB≌Rt△ADC,（HL）
AB=AC,AD=AD,
3. 已知：如图，在△ABC和△DEF中,AP、DQ分别是高,并且AB=DE,AP=DQ,∠BAC=∠EDF.求证：△ABC≌△DEF.
∠BAC=∠EDF, AB=DE,∠B=∠E
Rt△ABP≌Rt△DEQ
要证：AB=DE,AP=DQ
证明：∵AP、DQ是△ABC和△DEF的高, ∴∠APB=∠DQE=90°. 在Rt△ABP和Rt△DEQ中,
∴Rt△ABP≌Rt△DEQ ,(HL)∴ ∠B=∠E. 在△ABC和△DEF中,
∠BAC=∠EDF, AB=DE,∠B=∠E,
∴△ABC≌△DEF. (ASA)
已知：如图，在△ABC和△DEF中,AP、DQ分别是高,并且AB=DE,AP=DQ,∠BAC=∠EDF.求证：△ABC≌△DEF.
变式1：若把∠BAC＝∠EDF,改为BC＝EF ，△ABC与△DEF全等吗？请说明思路。
△ABC≌△DEF(SAS)
BC=EF, AB=DE,∠B=∠E
Rt△ABP≌Rt△DEQ(HL)
AB=DE,AP=DQ
变式2：若把∠BAC＝∠EDF,改为AC=DF，△ABC与△DEF全等吗？请说明思路.
AC=DF, AB=DE,∠B=∠E
变式3：请你把例题中的∠BAC＝∠EDF改为另一个适当条件，使△ABC与△DEF仍能全等.试说明思路.
△ABC≌△DEF(AAS)
∠C=∠F, AB=DE,∠B=∠E
灵活运用各种方法证明直角三角形全等.