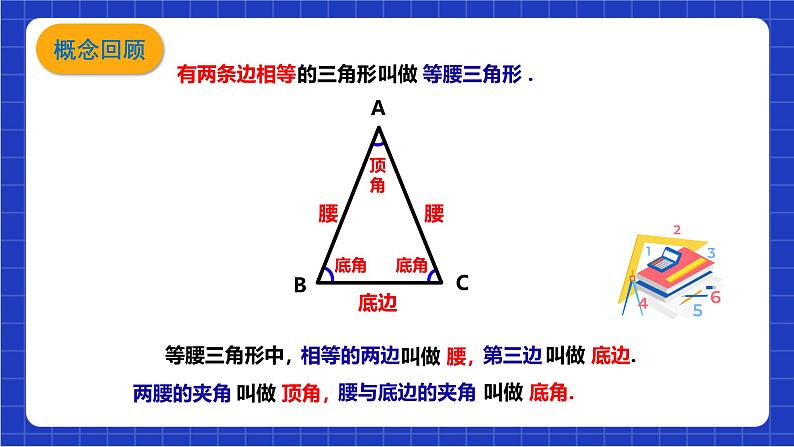
沪科版（2024）八年级上册第15章 轴对称图形和等腰三角形15.3 等腰三角形优秀ppt课件

这是一份沪科版（2024）八年级上册第15章 轴对称图形和等腰三角形15.3 等腰三角形优秀ppt课件，共35页。PPT课件主要包含了概念回顾，为什么不一样，巩固练习等内容，欢迎下载使用。

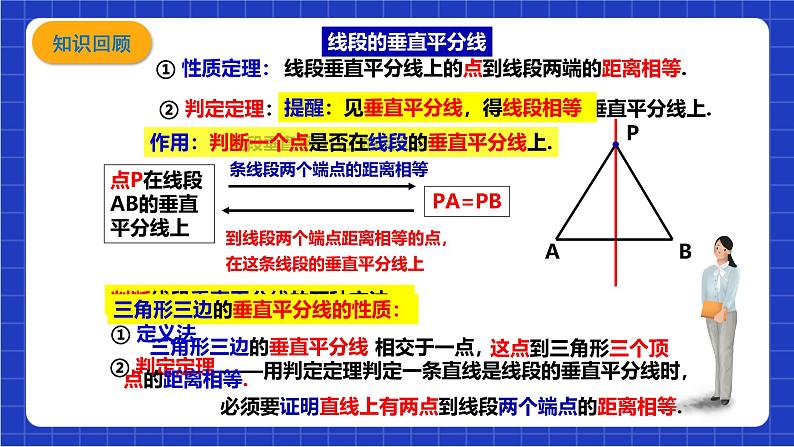
线段垂直平分线上的点到线段两端的距离相等.
到线段两端距离相等的点在线段的垂直平分线上.
点P在线段AB的垂直平分线上
到线段两个端点距离相等的点，在这条线段的垂直平分线上
线段垂直平分线上的点到这条线段两个端点的距离相等
判断线段垂直平分线的两种方法：
——用判定定理判定一条直线是线段的垂直平分线时，必须要证明直线上有两点到线段两个端点的距离相等.
三角形三边的垂直平分线的性质：
三角形三边的垂直平分线
这点到三角形三个顶点的距离相等.
提醒：见垂直平分线，得线段相等
作用：判断一个点是否在线段的垂直平分线上.
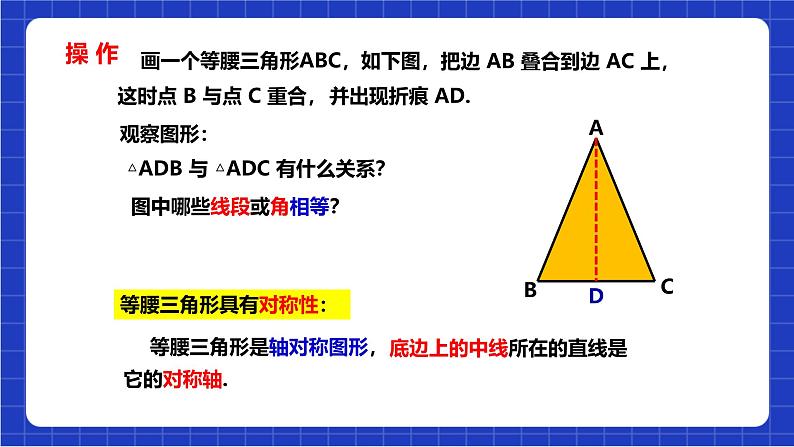
底边上的中线所在的直线是它的对称轴.
画一个等腰三角形ABC，如下图，
把边 AB 叠合到边 AC 上，
这时点 B 与点 C 重合，
图中哪些线段或角相等？
△ADB 与 △ADC 有什么关系？
等腰三角形是轴对称图形，
等腰三角形具有对称性：
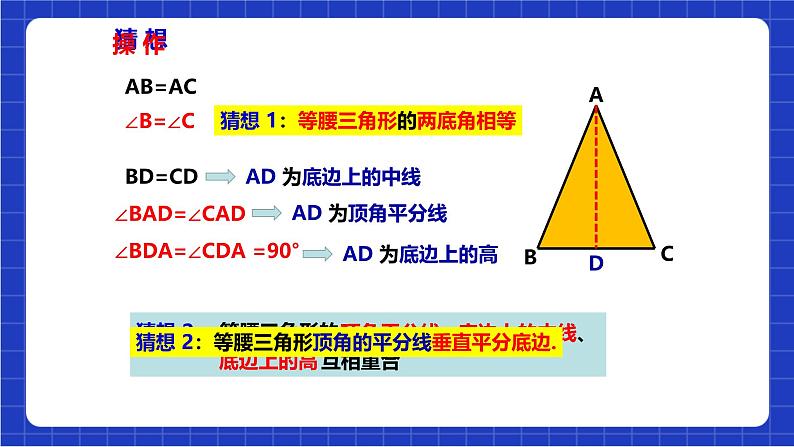
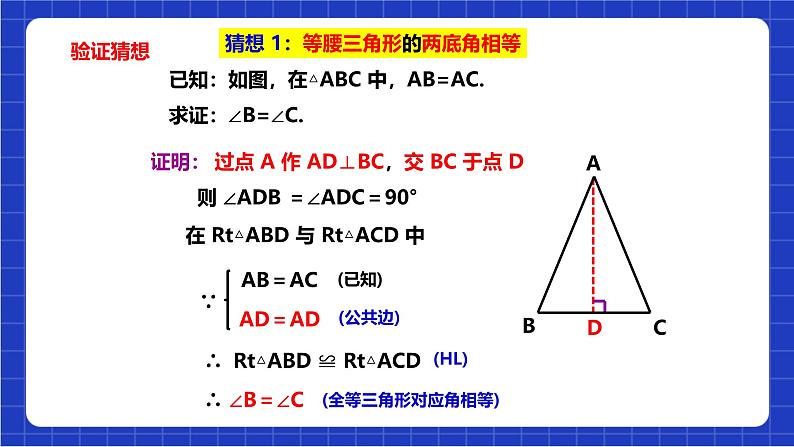
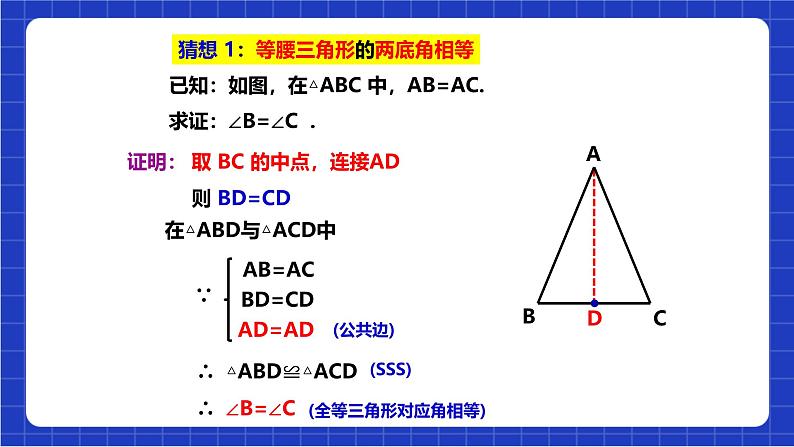
猜想 1：等腰三角形的两底角相等
猜想 2： 等腰三角形的
猜想 2：等腰三角形顶角的平分线垂直平分底边.
已知：如图，在△ABC 中，AB=AC.求证：∠B=∠C.
过点 A 作 AD⊥BC，交 BC 于点 D
则 ∠ADB ＝∠ADC＝90°
在 Rt△ABD 与 Rt△ACD 中
∴ Rt△ABD ≌ Rt△ACD
(全等三角形对应角相等)
已知：如图，在△ABC 中，AB=AC.求证：∠B=∠C .
取 BC 的中点，连接AD
在△ABD与△ACD中
∴ △ABD≌△ACD
作顶角 ∠BAC 的平分线 AD，交 BC 于点 D
则 ∠BAD=∠CAD
等腰三角形的两个底角相等.
∵ 在 △ABC 中，AB=AC
必须在同一个三角形中.
是证明角相等的常用方法，应用它证角即可省去三角形全等的证明，因而更简便.
已知：如图，在△ABC 中，AB=AC，∠BAD=∠CAD.
∠BDA=∠CDA=90°，
在 △ABD 与 △ACD 中
又∵ ∠BDA+∠CDA=180°
∴ ∠BDA=∠CDA=90°
等腰三角形顶角的平分线垂直平分底边
① ∵ 在△ABC中，AB＝AC，
② ∵ 在△ABC中，AB＝AC，
∴ ∠BAD=∠CAD ，
③ ∵ 在△ABC中，AB＝AC，
思考： 在等腰三角形中，若出现“三线”中的“一线”，我们应该想到什么？
(1) 必须是等腰三角形
(2) 必须是顶角的平分线、底边上的中线 和底边上的高才互相重合.
是证明线段相等、角相等、线段垂直等关系的重要方法.
画出任意一个等腰三角形的底角平分线、这个底角所对的腰上的中线和高，看看它们是否重合？
“三线合一”必须是等腰三角形的顶角平分线，底边上的中线和底边上的高互相重合
问题 1：等边三角形的三个内角之间有什么关系？
∠A=∠B=∠C=60°
猜想 3：等边三角形三个内角相等，每一个内角都等于60°.
已知：AB=AC=BC. 求证：∠A= ∠ B=∠C= 60°.
∵ ∠A+∠B+∠C=180°
∴ ∠A=∠B=∠C=60°
(三角形的内角和等于180°)
等边三角形三个内角相等，每一个内角都等于60°.
∵ △ABC 是等边三角形
∴ ∠A=∠B=∠C=60° AB=AC=BC
问题 2 等边三角形有“三线合一”的性质吗？等边三角形有几条对称轴？
顶角的平分线、底边上的高底边上的中线三线合一
① 等边三角形各边上的高、中线和所对角的平分线都“三线合一”.
② 等边三角形是特殊的等腰三角形，具备等腰三角形的所有性质.
1、若等腰三角形的底角是40°，则其顶角为_______.
3、若等腰三角形的一个内角是100°，则另外两个角 分别为__________________.
2、如果等腰三角形有一个内角等于80°，那么这个三角形的最小内角等于 .
4、已知：如图，在 △ABC 中，AB＝AC，∠BAC＝120º，点 D ，E 是底边上两点，且 BD＝AD，CE＝AE，求 ∠DAE 的度数.
又∵ ∠BAC＝120º
= ×(180°-120°)
∵ BD＝AD，CE＝AE
∴ ∠BAD＝∠B=30°
∠CAE＝∠C=30°
＝120°-30°-30°
∵ ∠BAC＝120°
∴ ∠B+∠C=180°-∠BAC=60°
∴ ∠BAD+∠CAE=60°
-(∠BAD+∠CAE)
变式：已知：如图，在 △ABC 中，AB＝AC，∠BAC＝120º，点 D ，E 是底边上两点，且 BD＝AD，CE＝AE，求 ∠DAE 的度数.
5、如图所示，在 △ABC 中，AB，AC 的垂直平分线分别交BC 于 D，E，垂足分别是 M，N．(1) 若 △ADE 的周长为 6，求 BC 的长；(2)若 ∠BAC=100°，求 ∠DAE 的度数．
6、如图所示，已知点 D，E 在 △ABC 的边 BC 上，AB＝AC，AD＝AE. 求证：BD＝CE.
过 A 点作 AF⊥BC，
∴ BF－DF＝CF－EF
作等腰三角形的顶角平分线、
等腰三角形中常见的添辅助线的方法是什么？
等腰三角形中常见的添辅助线的方法是：
7、如图，△ABC是等边三角形，E是AC上一点，D是BC延长线上一点，连接BE，DE，若∠ABE＝40°，BE＝DE，求∠CED的度数．
方法总结：等边三角形是特殊的三角形，它的三个内角都是60°，这个性质常应用在求三角形角度的问题上，一般需结合”等边对等角”、三角形的内角和与外角的性质.
∵ △ABC是等边三角形
∴ ∠ABC＝∠ACB＝60°
∴ ∠EBC＝∠ABC－∠ABE
∴ ∠D＝∠EBC＝20°
又∵ ∠ACB是△CED的外角
然后根据等腰三角形的性质
及三角形的外角和内角之间的关系，
8、 如图，在 △ABC 中 ，AB=AC，点 D 在 AC 上，且BD=BC=AD，求 △ABC 各角的度数.
一般采用方程思想来解决，
一般设较小的角的度数为 x .
用含未知数的代数式表示出一个三角形的内角的度数，
再利用三角形的内角和等于180°列出方程，
(三角形的外角等于与它不相邻的两个内角的和)
8、 如图，在 △ABC 中 ，AB=AC，点 D 在 AC 上，且BD=BC=AD，求 △ABC 各角的度数.
∴ x+2x+2x=180°
∠A+∠ABC+∠ACB=180°
使点A与点A′、点C与点C′重合，
9、求证：斜边和一条直角边分别相等的两个直角三角形全等。
已知：如图，在Rt△ABC和Rt△A′B′C′中，
求证：Rt△ABC≌Rt△A′B′C′.
点B和点B'在AC的两侧.
在平面内移动Rt△ABC和Rt△A'B'C',
∴ ∠BCB'=90°+90°=180°
∵ ∠ACB＝∠A'C′B'＝90º
∴ B，C，B'三点在一条直线上
∵ 在△ABB'中，AB=A'B'
在Rt△ABC和Rt△A'B'C'中
∠ACB＝∠A'C′B'
∴Rt△ABC≌Rt△A'B'C'
∠C＝∠C′＝90º，
AB＝A′B′，AC＝A′C′.
10、已知：如图，∠AOB=15°，并且OA=AB=BC=CD. 求证：∠1的度数.
∴ ∠ABO=∠AOB
∴ ∠ACB=∠BAC
∴ ∠BDC=∠CBD
=15°＋45°=60°
11、△ABC 为正三角形，点 M 是 BC 边上任意一点，点 N 是CA 边上任意一点，且 BM＝CN，BN 与 AM 相交于 Q 点，∠BQM 等于多少度？
∵ △ABC为正三角形
∴ ∠ABC＝∠C＝∠BAC＝60°，
在 △ABM 和 △BCN 中
∴ △AMB≌△BCN
∴ ∠BAM＝∠CBN
又∵ ∠BQM是△ABQ的外角
12、如图，在△ABC中，AB=AC，点D，E分别在AC，AB边上，且BC=BD，AD=DE=EB，求∠A的度数.
∴ ∠BDE=∠EBD
∴ 2x+3x+3x=180°
∠A+∠ABC+∠C=180°
13、如图：△ABC中，AB=AC，D 为 BC 边的中点，DE⊥AB. (1) 求证：∠BAC=2∠EDB； (2) 若AC=6，DE=2，求△ABC的面积．
14、A、B是4×4网格中的格点，网格中的每个小正方形的边长为1，请在图中清晰标出使以 A、B、C 为顶点的三角形是等腰三角形的所有格点C的位置．
分别以 A、B、C 为顶角顶点来分类讨论！
① 等边三角形三个内角相等，每一个内角都等于60°.
② 等边三角形各边上的高、中线和所对角的平分线都“三线合一”
③ 等边三角形是特殊的等腰三角形，具备等腰三角形的所有性质.
等腰三角形中常见的添辅助线的方法是： 作等腰三角形的顶角平分线、底边上的中线和底边上的高.