数学9.10 整式的乘法获奖ppt课件

这是一份数学9.10 整式的乘法获奖ppt课件，共28页。PPT课件主要包含了单项式与单项式相乘，单项式与多项式相乘，单项式乘多项式的法则，例题1计算，解原式＝，当a＝－2时，＝－20a2＋9a，x2-3xy2，整式的乘法，单项式乘多项式等内容，欢迎下载使用。

1、经历探索整式乘法的法则的过程2、能正确的进行整式的乘法运算。3、能应用本节所学知识解决实际问题
第1课时 单项式与单项式、多项式相乘
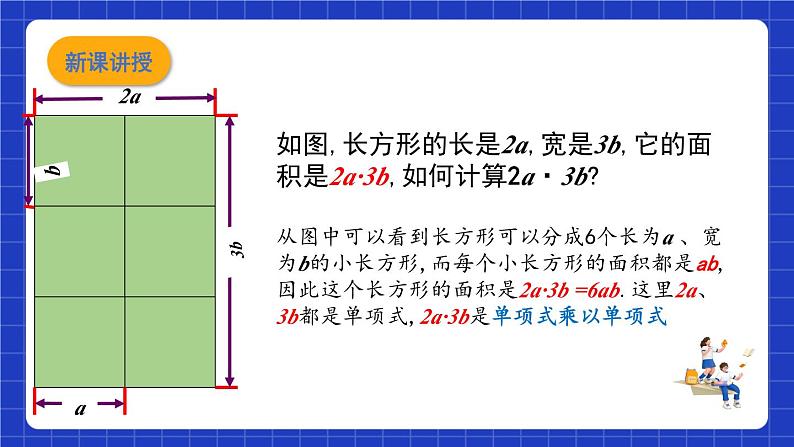
如图,长方形的长是2a,宽是3b,它的面积是2a·3b,如何计算2a·3b?从图中可以看到长方形可以分成6个长为a 、宽为b的小长方形,而每个小长方形的面积都是ab,因此这个长方形的面积是2a·3b =6ab.这里2a、3b都是单项式,2a·3b是单项式乘以单项式
2a·3b=(2×3)×(a· b)=6ab.
运用乘法交换律、结合律计算可得
同样，6a2 ·4ab=(6×4)(a2·a)·b =24a3b.
根据以上计算，想一想如何计算单项式乘单项式？
单项式与单项式相乘，把它们的系数、同底数幂分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式.
单项式与单项式的乘法法则
解：原式 = (3×4)(x·x3) = 12x4.
(3) (-4ax2)·(-3a2x3) ； (4) (-2x)3·(5x2y)2 .
解：原式 =[(-4)×(-3)] (a·a2)(x2·x3) = 12a3x5.
解：原式 = (-8x3)·(25x4y2) = (-8×25)·(x3·x4)·y2 =-200x7y2
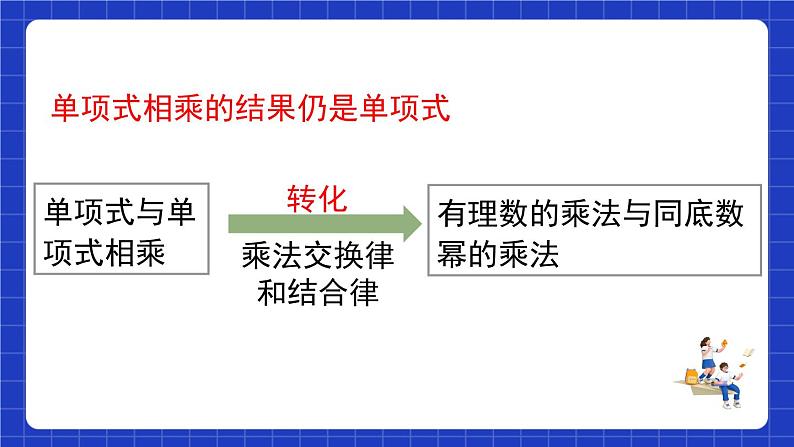
单项式相乘的结果仍是单项式
有理数的乘法与同底数幂的乘法
方法总结：(1) 在计算时，应先进行符号运算，积的系数等于各因式系数的积；(2) 注意按顺序运算；(3) 不要漏掉只在一个单项式里含有的字母因式；(4) 此性质对于多个单项式相乘仍然成立．
(1) 3x2 · 5x3； (2) 4y · (-2xy2)；
解：原式 = [4×(-2)](y · y2)·x = -8xy3.
(3) (-x)3 · (x2y)2； 解：原式 = (-x3) · (x4y2) = -x7y2.
解：原式 = (3×5)(x2 · x3) = 15x5.
单独因式 x 别漏乘漏写
(4) (-2a)3(-3a)2. 解：原式 = -8a3·9a2 = [(-8)×9](a3·a2) = -72a5.
下面计算结果对不对？如果不对，应当怎样改正？ (1) 3a3 · 2a2 = 6a6 ( ) 改正： . (2) 2x2 · 3x2 = 6x4 ( ) 改正： . (3) 3x2 · 4x2 =12x2 ( ) 改正： . (4) 5y3 · 3y5 = 15y15 ( ) 改正： .
3a3 · 2a2 = 6a5
3x2 · 4x2 = 12x4
5y3 · 3y5 = 15y8
例题3 已知 －2x3m＋1y2n 与 7xn－6y－3－m 的积与 x4y 是同类项，求 m2＋n 的值．
∴ m2 + n = 7.
方法总结：单项式乘单项式就是把它们的系数和同底数幂分别相乘，结合同类项的定义，列出二元一次方程组求出参数的值，然后代值计算即可．
如何计算是 (a＋3)·(2b)?这里a＋3是多项式, 2b是单项式,(a＋3)·(2b)是单项式与多项式相乘.运用乘法分配律、交换律计算,可以得到(a＋3)·(2b)= a·2b+3·2b=2ab+6b.
长方形的长是a＋3,宽是2b,它的面积是(a＋3)·(2b),把这个长方形如图分成两个小长方形，它们的面积分别是2ab与 6b,可知长方形的面积为2ab+6b,验证了上面计算的结果正确.
同样， -3x· (ax2－2x)= ( -3x)· ( ax2)+ ( -3x)· ( -2x)=-3ax3+6x2
单项式与多项式相乘，就是用单项式乘多项式的每一项，再把所得的积相加.
(1) 2ab·(3a2b －2ab2)；
＝ 6a3b2－4a2b3.
解：原式＝ 2ab · 3a2b + 2ab · (－2ab2)
例题2 先化简，再求值：3a(2a2－4a＋3)－2a2(3a＋4)， 其中 a＝－2.
解：3a(2a2－4a＋3)－2a2(3a＋4)
＝ 6a3－12a2＋9a－6a3－8a2
原式＝－20×4－9×2＝－98.
方法总结：在做乘法运算时，一定要注意单项式和多项式中每一项的符号，不要乘错．
例题3 如果(－3x)2(x2－2nx＋2)的展开式中不含 x3 项，求常数 n 的值．
方法总结：在整式乘法的混合运算中，要注意运算顺序. 注意当多项式中不含有哪一项时，则表示这一项的系数为 0.
解：(－3x)2(x2－2nx＋2)
＝ 9x2(x2－2nx＋2)
＝ 9x4－18nx3＋18x2.
∵ 展开式中不含 x3 项，∴ n＝0.
1. 计算 3a2 · 2a3 的结果是 ( ) A. 5a5 B. 6a5 C. 5a6 D. 6a6
2. 计算 (-9a2b3)·8ab2 的结果是 ( ) A. -72a2b5 B. 72a2b5 C. -72a3b5 D. 72a3b5
3. 若 (ambn) · (a2b) = a5b3，则 m + n = ( ) A. 8 B. 7 C. 6 D. 5
(1) 4(a - b + 1) = ____________；
4a - 4b + 4
(2) 3x(2x - y2) = __________；
(3) (2x - 5y + 6z)(-3x) = ________________；
-6x2 + 15xy - 18xz
(4) (-2a2)2(-a - 2b + c) = _________________.
-4a5 - 8a4b + 4a4c
5. 计算：－2x2·(xy + y2)－5x(x2y－xy2).
解：原式 = (-2x2)·xy + (-2x2)·y2 + (-5x)·x2y + (-5x)·(-xy2)
= -2x3y + (-2x2y2) + (-5x3y) + 5x2y2
= -7x3y + 3x2y2.
6. 解方程：8x(5－x) = 34－2x(4x－3).
解得 x = 1.
解：去括号，得 40x－8x2 = 34－8x2 + 6x.
移项，得 40x－6x = 34.
合并同类项，得 34x = 34.
7. 如图，一块长方形地用来建造住宅、广场、商厦， 求这块地的总面积.
解：4a [(3a + 2b) + (2a－b)]＝ 4a (5a + b)＝ 4a · 5a + 4a · b＝ 20a2 + 4ab.答：这块地的总面积为(20a2 + 4ab).
8. 某同学在计算一个多项式乘 －3x2 时，算成了加上 －3x2，得到的答案是 x2－2x＋1，那么正确的计算结果是多少？
解：设这个多项式为 A，则
∴ A＝4x2－2x＋1.
∴ A · (－3x2) ＝ (4x2－2x＋1)(－3x2)
A＋(－3x2)＝x2－2x＋1，
＝－12x4＋6x3－3x2.
实质上是转化为单项式×单项式
(1) 计算时，要注意符号问题，多项式中每一项都包括它前面的符号，单项式分别与多项式的每一项相乘时，同号相乘得正，异号相乘得负；(2) 不要出现漏乘现象； (3) 运算顺序不要出错：先乘方，再乘除，最后加减；(4) 对于混合运算，最后应合并同类项.
实质上是转化为同底数幂的运算