初中数学沪教版（五四制）（2024）七年级上册9.11 平方差公式精品课件ppt

这是一份初中数学沪教版（五四制）（2024）七年级上册9.11 平方差公式精品课件ppt，共20页。PPT课件主要包含了目标导航，y2－22，－a2，2a2－b2，新课讲授，a2−b2，公式变形，平方差公式，归纳总结，适当交换等内容，欢迎下载使用。
1.经历平方差公式的探索及推导过程，掌握平方差公式的结构特征．2.灵活应用平方差公式进行计算和解决实际问题．重点：掌握平方差公式的结构特征．难点：应用平方差公式进行计算和解决实际问题．
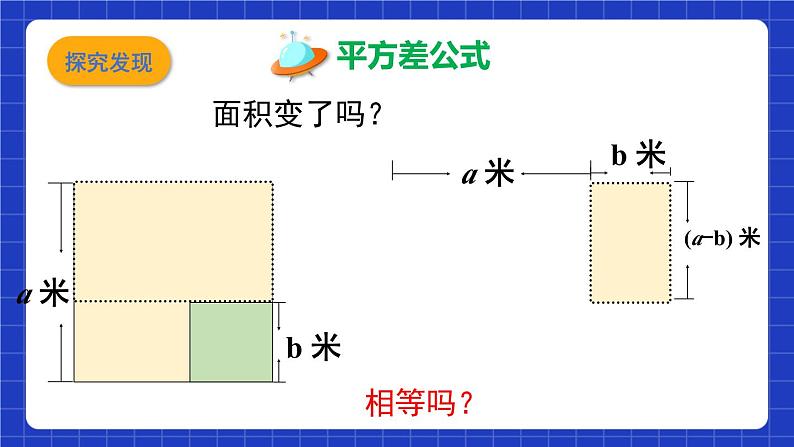
思考计算下列各题,并观察下列乘式与结果的特征(1)(y+2)(y-2)=(2)(3-a)(3+a)=(3)(2a+b)(2a-b)=通过计算你发现了什么规律?比较等号两边的代数式可以看到
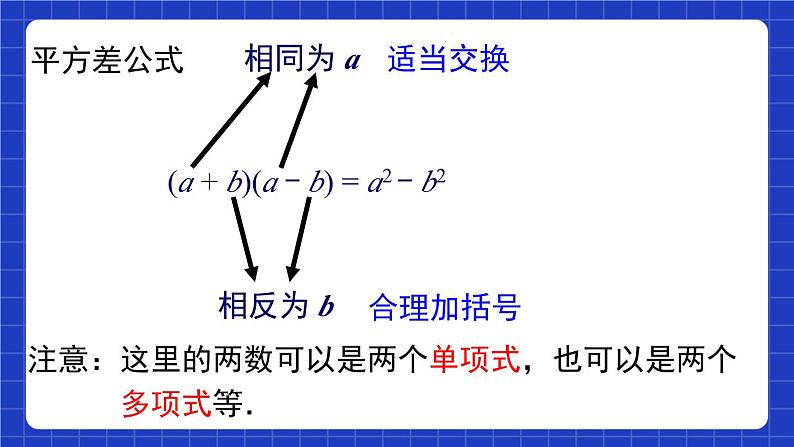
(a + b)(a − b) =
两数和与这两数差的积，等于这两数的平方差.
1. (a – b)(a + b) = a2 – b2；
2. (b + a)(–b + a) = a2 – b2.
注意：这里的两数可以是两个单项式，也可以是两个 多项式等．
(a + b)(a - b) = a2 - b2
解：(1) 原式＝(2x)2－y2
解：(3) 原式＝(-x)2－(3y)2
例题1 计算：(3) (-x＋3y)(-x-3y)； (4) (2a＋b)(2a-b)(4a2＋b2)
(4) 原式＝(4a2－b2) (4a2 ＋ b2)
例题2 计算：(1) 102×98； (2)30.2×29.8.
解：(1) 原式 = (100＋2)(100－2)
(2) 原式 = (30＋0.2)×(30－0.2)
= 302－ 0.22
例题3 计算：(y + 2)(y – 2) – (y – 1)(y + 5) .
解：(y＋2)(y－2)－(y－1)(y＋5)
= y2－22－(y2＋4y－5)
= y2－4－y2－4y＋5
1. 下列运算中，可用平方差公式计算的是 (　　)A．(x＋y)(x＋y) B．(－x＋y)(x－y)C．(－x－y)(y－x) D．(x＋y)(－x－y)
2. 计算 (2x＋1)(2x－1) 等于 (　　)A．4x2－1 B．2x2－1 C．4x－1 D．4x2＋1
3. 两个正方形的边长之和为 5，边长之差为 2，那么用较大的正方形的面积减去较小的正方形的面积，差是______．
（1）(a + 3b)(a - 3b)；
解：原式 = (2a + 3)(2a－3)
= (2a)2－32
解：原式 = (-2x2 )2－y2
解：原式 = a2－(3b)2
（2）(3 + 2a)(－3 + 2a)；
（3）(－2x2－y)(－2x2 + y).
4. 利用平方差公式计算：
5. 计算： 20232－2022×2024.
20232－2022×2024
= 20232－(2023－1)(2023 + 1)
－(20232－12 )
= 20232－20232 + 12
6. 利用平方差公式计算：
（1）(x－2)(x ＋2)(x 2＋4)； 解：原式 = (x2－4)(x 2＋4) = x 4－16.
(2) (m－n)(m＋n)(m2＋n2)(m4＋n4).
解：原式 = (m2－n2)(m2＋n2)(m4＋n4)
= (m4－n4)(m4＋n4)
已知 x≠1，计算：(1＋x)(1－x)＝1－x2，(1－x)(1＋x＋x2)＝1－x3，(1－x)(1＋x＋x2＋x3)＝1－x4……(1) 观察以上各式并猜想：(1－x)(1＋x＋x2＋…＋xn)＝________( n 为正整数)；
(2) 根据你的猜想计算： ① (1－2)(1＋2＋22＋23＋24＋25)＝______； ② 2＋22＋23＋…＋2n＝__________ (n 为正整数)； ③ (x－1)(x99＋x98＋x97＋…＋x2＋x＋1)＝________；
(3) 通过以上规律请你进行下面的探索：① (a－b)(a＋b)＝_______；② (a－b)(a2＋ab＋b2)＝________；③ (a－b)(a3＋a2b＋ab2＋b3)＝________．
两个数的和与这两个数的差的积，等于这两个数的平方差
1. 字母表示：(a + b)(a－b) = a2－b2
2. 紧紧抓住 “一同一反”这一特征，在应用时，只有两个二项式的积才有可能应用平方差公式；不能直接应用公式的，要经过适当变形才可以应用