江苏省江阴市敔山湾实验学校2024年数学九年级第一学期开学学业水平测试模拟试题【含答案】

这是一份江苏省江阴市敔山湾实验学校2024年数学九年级第一学期开学学业水平测试模拟试题【含答案】，共19页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）若关于的一元二次方程通过配方法可以化成的形式，则的值不可能是
A．3B．6C．9D．10
2、（4分）若一个多边形的内角和等于720°，则这个多边形的边数是（ ）
A．5B．6C．7D．8
3、（4分）用反证法证明“三角形中至少有一个内角大于或等于60°”时，应先假设（ ）
A．有一个内角小于60°B．每一个内角都小于60°
C．有一个内角大于60°D．每一个内角都大于60°
4、（4分）如图，在中，，，，是边上的动点，，，则的最小值为（ ）
A．B．C．5D．7
5、（4分）若关于的一元二次方程的一个根是0，则的值是（ ）
A．1B．-1C．1或-1D．
6、（4分）大肠杆菌的长度平均约为0.0000014米，把这个数用科学记数表示正确的是（ ）米．
A．1.4×106B．1.4×10﹣5C．14×10﹣7D．1.4×10﹣6
7、（4分）一组从小到大排列的数据：a，3，5，5，6（a为正整数），唯一的众数是5，则该组数据的平均数是（ ）
A．4.2或4B．4C．3.6或3.8D．3.8
8、（4分）在▱ABCD中，∠C=32°，则∠A的度数为（ ）
A．148°B．128°C．138°D．32°
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图，⊙O是△ABC的外接圆，∠ACO=45°，则∠B的度数为_____.
10、（4分）如果多边形的每个内角都等于，则它的边数为______.
11、（4分）二次根式中字母 a 的取值范围是______．
12、（4分）如图，在Rt△ABC中，∠B＝90°，AB＝6，BC＝8，点D在线段BC上一动点，以AC为对角线的平行四边形ADCE中，则DE的最小值是______．
13、（4分）若关于的一元二次方程有两个相等的实数根，则的值是__________．
三、解答题（本大题共5个小题，共48分）
14、（12分）若m，n，p满足m－n=8，mn＋p2＋16=0，求m＋n＋p的值？
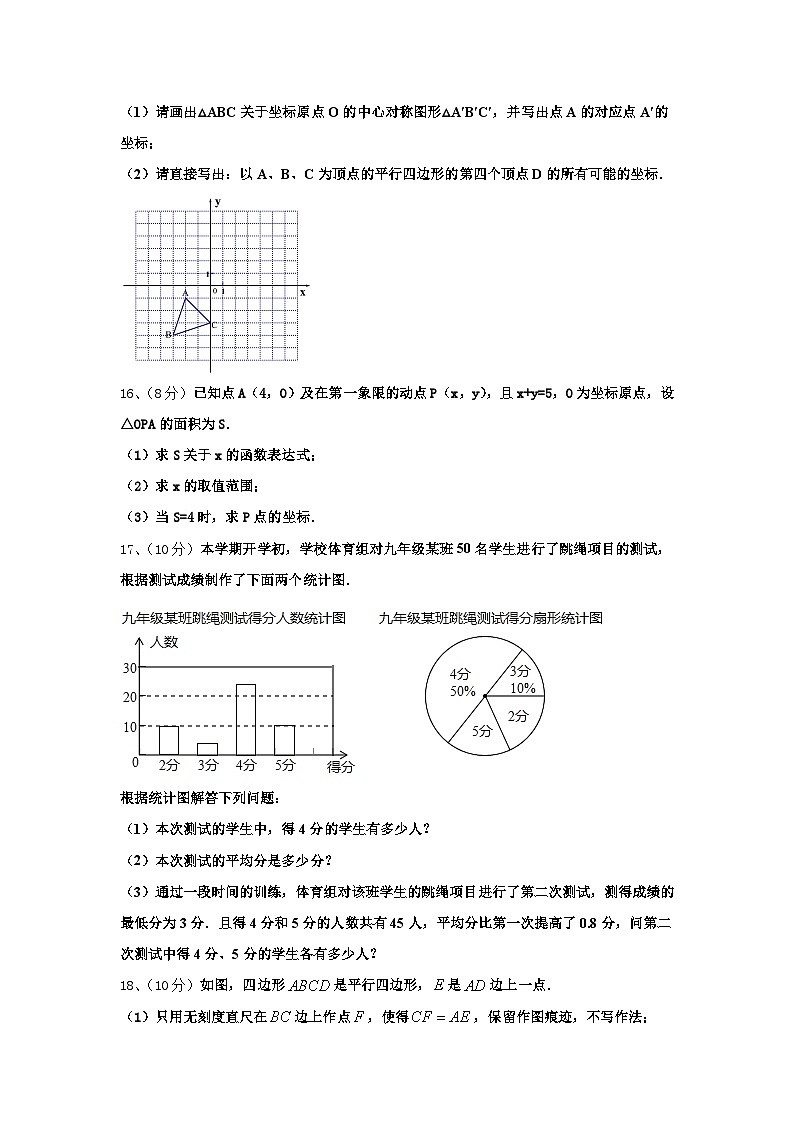
15、（8分）如图，在坐标系中，△ABC中A（-2，-1）、B（-3，-4）、C（0，-3）．
（1）请画出△ABC关于坐标原点O的中心对称图形△A′B′C′，并写出点A的对应点A′的坐标；
（2）请直接写出：以A、B、C为顶点的平行四边形的第四个顶点D的所有可能的坐标．
16、（8分）已知点A（4，0）及在第一象限的动点P（x，y），且x+y=5，0为坐标原点，设△OPA的面积为S．
（1）求S关于x的函数表达式；
（2）求x的取值范围；
（3）当S=4时，求P点的坐标．
17、（10分）本学期开学初，学校体育组对九年级某班50名学生进行了跳绳项目的测试，根据测试成绩制作了下面两个统计图．
根据统计图解答下列问题：
（1）本次测试的学生中，得4分的学生有多少人？
（2）本次测试的平均分是多少分？
（3）通过一段时间的训练，体育组对该班学生的跳绳项目进行了第二次测试，测得成绩的最低分为3分．且得4分和5分的人数共有45人，平均分比第一次提高了0.8分，问第二次测试中得4分、5分的学生各有多少人？
18、（10分）如图，四边形是平行四边形，是边上一点．
（1）只用无刻度直尺在边上作点，使得，保留作图痕迹，不写作法；
（2）在（1）的条件下，若，，求四边形的周长．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）如图，点A在双曲线y=上，AB⊥y轴于B，S△ABO =3，则k=__________
20、（4分）把多项式n（n﹣2）+m（2﹣n）分解因式的结果是_____．
21、（4分）已知正比例函数y=kx的图象经过点A（﹣1，2），则正比例函数的解析式为 ．
22、（4分）五子棋的比赛规则是：一人执黑子，一人执白子，两人轮流放棋，每次放一个棋子在棋盘的格点处，只要有同色的五个棋子先连成一条线(横、竖、斜均可)就获得胜利．如图是两人正在玩的一盘棋，若白棋A所在位置用坐标表示是(－2，2)，黑棋B所在位置用坐标表示是(0，4)，现在轮到黑棋走，黑棋放到点C的位置就获得胜利，则点C的坐标是__________．
23、（4分）若分式的值为0，则的值是 _____．
二、解答题（本大题共3个小题，共30分）
24、（8分）如图，直线l1：y=﹣2x与直线l2：y=kx+b在同一平面直角坐标系内交于点P．
（1）直接写出不等式﹣2x＞kx+b的解集______；
（2）设直线l2与x轴交于点A，△OAP的面积为12，求l2的表达式．
25、（10分）如图，四边形ABCD是正方形，G是BC上任意一点（点G与B、C不重合），AE⊥DG于E，CF∥AE交DG于F．请你经过观察、猜测线段FC、AE、EF之间是否存在一定的数量关系？若存在，证明你的结论；若不存在，请说明理由．
26、（12分）如图，在长方形ABCD中，AB=6，BC=8，点O在对角线AC上，且OA=OB=OC，点P是边CD上的一个动点，连接OP，过点O作OQ⊥OP，交BC于点Q.
（1）求OB的长度；
（2）设DP= x，CQ= y，求y与x的函数表达式（不要求写自变量的取值范围）；
（3）若OCQ是等腰三角形，求CQ的长度.
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、D
【解析】
方程配方得到结果，即可作出判断．
【详解】
解：方程，变形得：，
配方得：，即，
，即，
则的值不可能是10，
故选：．
此题考查了解一元二次方程配方法，熟练掌握完全平方公式是解本题的关键．
2、B
【解析】
试题分析：根据内角和定理180°×（n-2）即可求得．
解：180°×（n-2）=720°，解得n=1．
考点：多边形的内角和定理．
3、B
【解析】
根据反证法的第一步是假设结论不成立矩形解答即可．
【详解】
解：用反证法证明“三角形中至少有一个内角大于或等于”时，
第一步应先假设每一个内角都小于，
故选：．
本题考查的是反证法，解此题关键要懂得反证法的意义及步骤．反证法的步骤是：（1）假设结论不成立；（2）从假设出发推出矛盾；（3）假设不成立，则结论成立．
4、B
【解析】
先由矩形的判定定理推知四边形PECF是矩形；连接PC，则PC=EF，所以要使EF，即PC最短，只需PC⊥AB即可；然后根据三角形的等积转换即可求得PC的值．
【详解】
如图，连接PC．
∵在△ABC中，AC=6，BC=8，AB=10，
∴AB2=AC2+BC2，
∴∠C=90°．
又∵PE⊥AC于点E，PF⊥BC于点F．
∴∠CEP=∠CFP=90°，
∴四边形PECF是矩形．
∴PC=EF．
∴当PC最小时，EF也最小，
即当PC⊥AB时，PC最小，
∵BC•AC=AB•PC，即PC=，
∴线段EF长的最小值为.
故选B．
本题考查了勾股定理、矩形的判定与性质、垂线段最短．利用“两点之间垂线段最短”找出PC⊥AB时，PC取最小值是解答此题的关键．
5、B
【解析】
根据一元二次方程的解的定义把x=0代入方程得到关于a的一元二次方程，然后解此方程即可
【详解】
把x=0代入方程得，解得a=±1．
∵原方程是一元二次方程，所以 ，所以,故
故答案为B
本题考查了一元二次方程的解的定义：使一元二次方程左右两边成立的未知数的值叫一元二次方程的解．
6、D
【解析】
绝对值小于1的正数也可以利用科学记数法表示，一般形式为(为整数)，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．
【详解】
．
故选：D．
本题主要考查了科学记数法的表示，熟练掌握相关表示方法是解决本题的关键.
7、A
【解析】
根据题意得出正整数a的值，再根据平均数的定义求解可得．
【详解】
解：∵数据：a，3，5，5，6（a为正整数），唯一的众数是5，
∴a＝1或a＝2，
当a＝1时，平均数为：；
当a＝2时，平均数为：；
故选：A．
本题主要考查了平均数的求法，根据数据是从小到大排列得出a的值是解题的关键．
8、D
【解析】
根据平行四边形的性质：对角相等即可求出的度数.
【详解】
四边形是平行四边形，
，
，
.
故选：.
本题考查平行四边形的性质，比较简单，解答本题的关键是掌握平行四边形的对角相等.
二、填空题（本大题共5个小题，每小题4分，共20分）
9、45°
【解析】
如图，连接OA，因OA=OC，可得∠ACO=∠OAC=45°，根据三角形的内角和公式可得∠AOC=90°，再由圆周角定理可得∠B=45°.
10、1
【解析】
先求出这个多边形的每一个外角的度数，再用360°除以外角的度数即可得到边数．
【详解】
∵多边形的每一个内角都等于150°，∴多边形的每一个外角都等于180°﹣150°=30°，∴边数n=360°÷30°=1．
故答案为：1．
本题考查了多边形的内角与外角的关系，求出每一个外角的度数是解答本题的关键．
11、.
【解析】
运用二次根式中的被开方数的非负性进行求解即可，即有意义，则a≥0.
【详解】
解：由题意得2a+5≥0，解得：.
故答案为.
本题考查了二次根式的意义和性质，对于二次根式而言，关键是要注意两个非负性：一是a≥0，二是≥0；在各地试卷中是高频考点.
12、1
【解析】
平行四边形ADCE的对角线的交点是AC的中点O，当OD⊥BC时，OD最小，即DE最小，根据三角形中位线定理即可求解．
【详解】
解：平行四边形ADCE的对角线的交点是AC的中点O，当OD⊥BC时，OD最小，即DE最小．
∵OD⊥BC，BC⊥AB，
∴OD∥AB，
又∵OC=OA，
∴OD是△ABC的中位线，
∴OD=AB=3，
∴DE=2OD=1．
故答案为：1．
本题考查了三角形中位线的性质，即三角形的中位线平行于第三边且等于第三边的一半，正确理解DE最小的条件是关键．
13、1
【解析】
因为关于的一元二次方程有两个相等的实数根，故 ，代入求解即可.
【详解】
根据题意可得： 解得：m=1
故答案为：1
本题考查的是一元二次方程的根的判别式，掌握根的判别式与方程的根的关系是关键.
三、解答题（本大题共5个小题，共48分）
14、m＋n＋p＝0.
【解析】
试题分析:把m,n,p看成是未知数,本题已知两个方程求三个未知数,因此可以采用主元法,将其中一个未知数看成常数,另外两个当作未知数进行解答,本题由m－n＝8,可得:
m＝n＋8,把m＝n＋8代入mn＋p2＋16＝0,得n2＋8n＋16＋p2＝0,即(n＋4)2＋p2＝0,根据非负数的非负性质可求出n=－4,p=0,所以m=4,因此m＋n＋p＝4＋(－4)＋0＝0.
因为m－n＝8，所以m＝n＋8.
将m＝n＋8代入mn＋p2＋16＝0中，得n(n＋8)＋p2＋16＝0，所以n2＋8n＋16＋p2＝0，即(n＋4)2＋p2＝0.
又因为(n＋4)2≥0，p2≥0，
所以，解得，所以m＝n＋8＝4，
所以m＋n＋p＝4＋(－4)＋0＝0.
15、（1）画图略，A’（2,1）（2）（1，0）或（－1，－6）或（－5，－2）
【解析】
（1）找到三角形各顶点与原点对称点，再连接各点即可；
（2）根据平行四边形的性质即可在直角坐标系中找到D点.
【详解】
（1）如图，△A′B′C′为所求，A’（2,1）
（2）如图，D的坐标为（1，0）或（－1，－6）或（－5，－2）
此题主要考查坐标与图形，解题的关键是熟知直角坐标系的坐标特点.
16、（1）S=10﹣2x；（2）0＜x＜5；（3）（3，2）
【解析】
(1)根据题意画出图形,由x＋y＝5可知y＝5﹣x ,再由三角形的面积公式即可得出结论;
(2)由点P（x，y）在第一象限,且x＋y＝5得出x的取值范围即可;
(3)把S＝4代入(1)中的关系式求出x的值,进而可得出y的值.
【详解】
（1）如图：
∵x＋y＝5，
∴y＝5﹣x，
∴S＝×4×（5﹣x）＝10﹣2x；
（2）∵点P（x，y）在第一象限，且x＋y＝5，
∴0＜x＜5；
（3）∵由（1）知，S＝10﹣2x，
∴10﹣2x＝4，解得x＝3，
∴y＝2，
∴P（3，2）．
本题考查的是一次函数的性质,根据题意画出图形,利用数形结合求解是解答此题的关键.
17、（1）25人
（2）37分
（3）第二次测试中得4分的学生有15人、得5分的学生有30人．
【解析】
（1）根据频数、频率和总量的关系：频数=总量频率计算即可．
（2）平均数是指在一组数据中所有数据之和再除以数据的个数，据此计算即可．
（3）设第二次测试中得4分的学生有x人、得5分的学生有y人，根据“得4分和5分的人数共有45人”和“平均分比第一次提高了0.8分”列方程组求解即可．
【详解】
解：（1）本次测试的学生中，得4分的学生有人．
（2）本次测试的平均分平均分（分）．
（3）设第二次测试中得4分的学生有x人、得5分的学生有y人，
根据题意，得：，
解得：．
答：第二次测试中得4分的学生有15人、得5分的学生有30人．
18、 (1)见解析;(2)1.
【解析】
(1)如图，连接，交于点，作直线交于点，点即为所求；
(2)求出，即可解决问题．
【详解】
(1)如图，点即为所求；
(2)，，
，
，
，
，
四边形是平行四边形，
，，
平行四边形的周长为1．
本题考查作图——复杂作图，平行四边形的性质等知识，解题的关键是灵活运用所学知识解决问题.
一、填空题（本大题共5个小题，每小题4分，共20分）
19、6
【解析】
根据反比例函数系数k的几何意义得出S△ABO=|k|，即可求出表达式.
【详解】
解： ∵△OAB的面积为3，∴k＝2S△ABO＝6，
∴反比例函数的表达式是y=
即k=6
本题考查反比例函数系数k的几何意三角形面积=|k|，学生们熟练掌握这个公式.
20、（n﹣2）（n﹣m）．
【解析】
用提取公因式法分解因式即可．
【详解】
n（n﹣2）+m（2﹣n）= n（n﹣2）-m（n-2）=（n﹣2）（n﹣m）．
故答案为（n﹣2）（n﹣m）．
本题考查了用提公因式法进行因式分解；一个多项式有公因式首先提取公因式，然后再用其他方法进行因式分解，同时因式分解要彻底，直到不能分解为止．
21、y=﹣1x
【解析】
试题分析：根据点在直线上点的坐标满足方程的关系，把点A的坐标代入函数解析式求出k值即可得解：
∵正比例函数y=kx的图象经过点A（﹣1，1），
∴﹣k=1，即k=﹣1．
∴正比例函数的解析式为y=﹣1x．
22、 (3，3)
【解析】
根据题意可以画出相应的平面直角坐标系，从而可以得到点C的坐标．
【详解】
由题意可得如图所示的平面直角坐标系，
故点C的坐标为（3，3），
故答案为（3，3）．
本题考查坐标确定位置，解题的关键是明确题意，建立合适的平面直角坐标系．
23、1
【解析】
分式值为零的条件：分子等于零且分母不等于零，由此列出不等式和等式，求解即可.
【详解】
∵分式的值为0，
∴,
∴x=1．
故答案是：1.
考查了分式的值为零的条件，解题关键是：分式值为零的条件是分子等于零且分母不等于零．
二、解答题（本大题共3个小题，共30分）
24、（1）x