江苏省南京联合体2024年九上数学开学教学质量检测模拟试题【含答案】

这是一份江苏省南京联合体2024年九上数学开学教学质量检测模拟试题【含答案】，共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
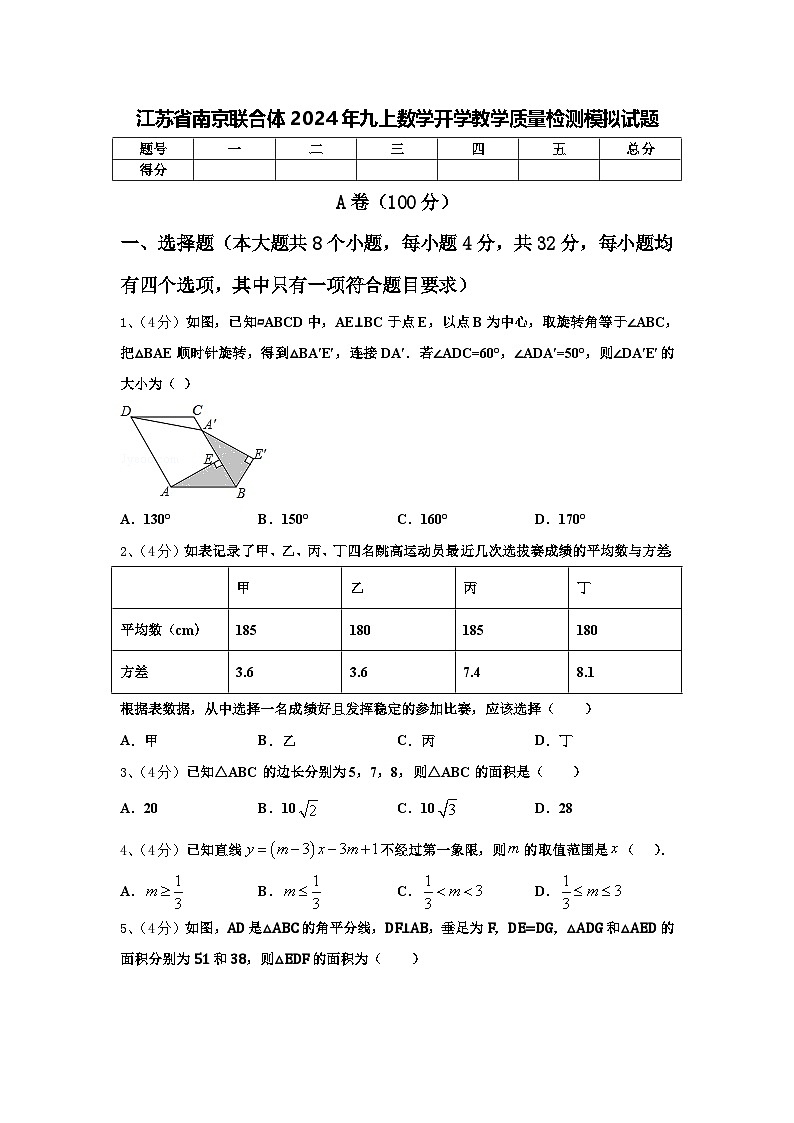
1、（4分）如图，已知▱ABCD中，AE⊥BC于点E，以点B为中心，取旋转角等于∠ABC，把△BAE顺时针旋转，得到△BA′E′，连接DA′．若∠ADC=60°，∠ADA′=50°，则∠DA′E′的大小为（ ）
A．130°B．150°C．160°D．170°
2、（4分）如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差：
根据表数据，从中选择一名成绩好且发挥稳定的参加比赛，应该选择（ ）
A．甲B．乙C．丙D．丁
3、（4分）已知△ABC的边长分别为5，7，8，则△ABC的面积是（ ）
A．20B．10C．10D．28
4、（4分）已知直线不经过第一象限，则的取值范围是（ ）．
A．B．C．D．
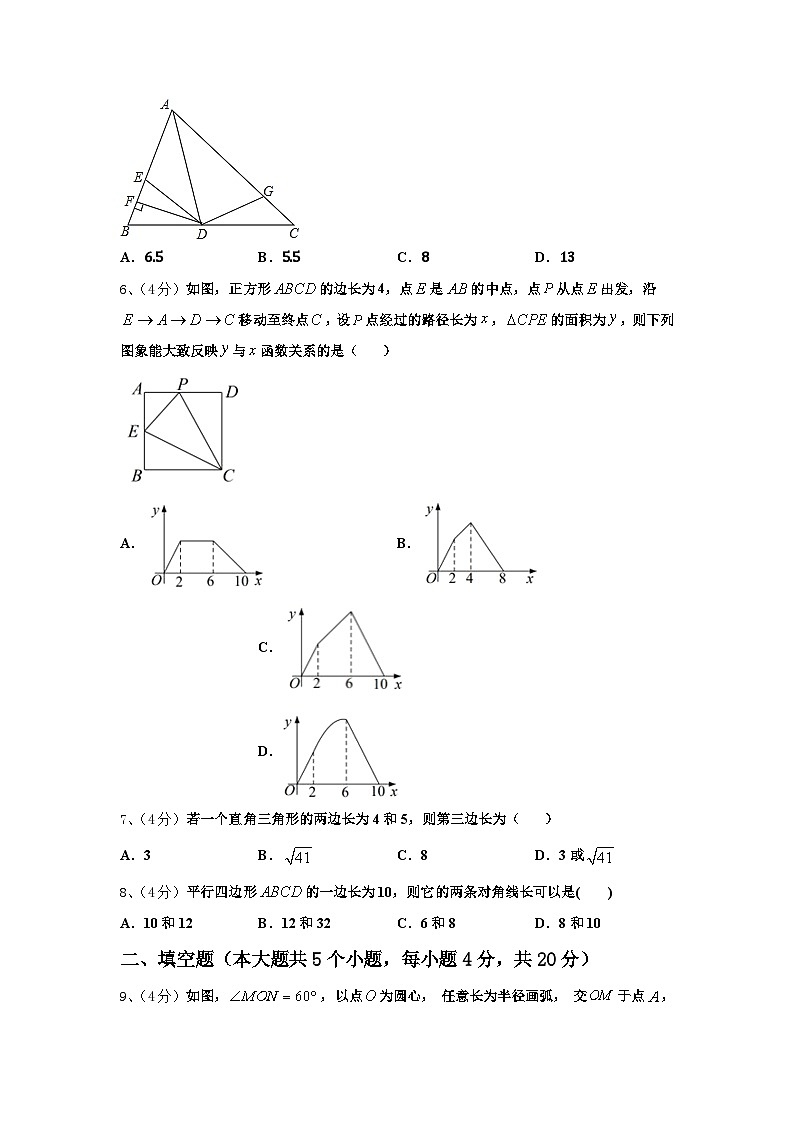
5、（4分）如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE=DG，△ADG和△AED的面积分别为51和38，则△EDF的面积为（ ）
A．6.5B．5.5C．8D．13
6、（4分）如图，正方形的边长为4，点是的中点，点从点出发，沿移动至终点，设点经过的路径长为，的面积为，则下列图象能大致反映与函数关系的是（ ）
A．B．C．D．
7、（4分）若一个直角三角形的两边长为4和5，则第三边长为（ ）
A．3B．C．8D．3或
8、（4分）平行四边形的一边长为10，则它的两条对角线长可以是( )
A．10和12B．12和32C．6和8D．8和10
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图，，以点为圆心， 任意长为半径画弧， 交于点，交于点，再分别以点、为圆心，大于长为半径画弧交于点，过点作射线，在射线上截取，过点作， 垂足为点， 则的长为________________．
10、（4分）如图，已知菱形OABC的顶点O(0，0)，B(2，2)，则菱形的对角线交点D的坐标为(1,1),若菱形绕点O逆时针旋转，每秒旋转45°，则第60秒时，点D的坐标为________．
11、（4分）如图，为的中位线，点在上，且为直角，若，，则的长为__________．
12、（4分）计算：的结果是________．
13、（4分）如图，直线y=与y=x交于A（3，1）与x轴交于B（6，0），则不等式组0的解集为_____．
三、解答题（本大题共5个小题，共48分）
14、（12分）一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为x（小时），两车之间的距离为（千米），图中的折线表示与的函数关系．
信息读取：
（1）甲、乙两地之间的距离为__________千米；
（2）请解释图中点的实际意义；
图像理解：
（3）求慢车和快车的速度；
（4）求线段所示的与之间函数关系式．
15、（8分）綦江区某中学的国旗护卫队需从甲、乙两队中选择一队身高比较整齐的队员担任护旗手，每队中每个队员的身高（单位：cm）如下:
乙队：
分析数据：两组样本数据的平均数、中位数、众数、方差如下表所示：
整理、描述数据:
（1）表中a=______，b=______，c=______；
（2）根据表格中的数据，你认为选择哪个队比较好？请说明理由．
16、（8分）在平面直角坐标系中，直线分别交轴，轴于点.
（1）当，自变量的取值范围是 （直接写出结果）；
（2）点在直线上.
①直接写出的值为 ；
②过点作交轴于点，求直线的解析式.
17、（10分）为了迎接“六一”国际儿童节，某童装品牌专卖店准备购进甲、乙两种童装，这两种童装的进价和售价如下表：
如果用5000元购进甲种童装的数量与用6000元购进乙种童装的数量相同．
（1）求m的值；
（2）要使购进的甲、乙两种童装共200件的总利润（利润＝售价﹣进价）不少于8980元，且甲种童装少于100件，问该专卖店有哪几种进货方案？
18、（10分）为了庆祝新中国成立70周年，某校组织八年级全体学生参加“恰同学少年，忆峥嵘岁月”新中国成立70周年知识竞赛活动．将随机抽取的部分学生成绩进行整理后分成5组，50～60分（）的小组称为“学童”组，60～70分()的小组称为“秀才”组，70～80分()的小组称为“举人”组，80～90分()的小组称为“进士”组，90～100分()的小组称为“翰林”组，并绘制了不完整的频数分布直方图如下，请结合提供的信息解答下列问题：
（1）若“翰林”组成绩的频率是12.5％，请补全频数分布直方图；
（2）在此次比赛中，抽取学生的成绩的中位数在 组；
（3）学校决定对成绩在70～100分()的学生进行奖励，若八年级共有336名学生，请通过计算说明，大约有多少名学生获奖?
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）若a，b都是实数，b＝+﹣2，则ab的值为_____．
20、（4分）若一元二次方程的两个实数根分别是、，则一次函数的图象一定不经过第____________象限.
21、（4分）如果P（2，m）,A (1, 1), B (4, 0)三点在同一直线上，则m的值为_________.
22、（4分）定义运算“”：a*b=a-ab,若,，a*b,则x的值为_________．
23、（4分）方程-x=1的根是______
二、解答题（本大题共3个小题，共30分）
24、（8分）先化简，再求值： ÷（1+），其中x=+1．
25、（10分）如图，在Rt△ABC中，∠C＝90°，AC＝5，AB＝13，求BC．
26、（12分）知y+3与5x+4成正比例，当x=1时，y=—18，
（1）求y关于x的函数关系。
（2）若点（m，—8）在此图像上，求m的值。
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、C
【解析】
根据平行四边形对角相等、邻角互补，得∠ABC=60°，∠DCB=120°，再由∠A′DC=10°，可运用三角形外角求出∠DA′B=130°，再根据旋转的性质得到∠BA′E′=∠BAE=30°，从而得到答案．
【详解】
∵四边形ABCD是平行四边形，∠ADC=60°，
∴∠ABC=60°，∠DCB=120°，
∵∠ADA′=50°，
∴∠A′DC=10°，
∴∠DA′B=130°，
∵AE⊥BC于点E，
∴∠BAE=30°，
∵△BAE顺时针旋转，得到△BA′E′，
∴∠BA′E′=∠BAE=30°，
∴∠DA′E′=∠DA′B+∠BA′E′=160°．
故选C．
考点：旋转的性质；平行四边形的性质．
2、A
【解析】
首先比较平均数，平均数相同时选择方差较小的运动员参加．
【详解】
∵=>=，
∴从甲和丙中选择一人参加比赛，
∵=<<，
∴选择甲参赛，
故选A．
此题主要考查了平均数和方差的应用，解题关键是明确平均数越高，成绩越高，方差越小，成绩越稳定.
3、C
【解析】
过A作AD⊥BC于D，根据勾股定理列方程得到BD，然后根据三角形的面积公式即可得到结论．
【详解】
如图，
∵AB=5，AC=7，BC=8，
过A作AD⊥BC于D，
∴AB2-BD2=AC2-CD2=AD2，
∴52-BD2=72-（8-BD）2，
解得：BD=，
∴AD=，
∴△ABC的面积=10，
故选C．
本题考查了勾股定理，三角形的面积的计算，熟练掌握勾股定理是解题的关键．
4、D
【解析】
试题解析：∵直线不经过第一象限，则有：
解得：．
故选．
5、A
【解析】
过点D作DH⊥AC于H，利用角平分线的性质得到DF=DH，将三角形EDF的面积转化为三角形DGH的面积来求．
【详解】
如图，过点D作DH⊥AC于H，
∵AD是△ABC的角平分线，DF⊥AB，
∴DF=DH，
在Rt△DEF和Rt△DGH中，
∴Rt△DEF≌Rt△DGH（HL），
∴S△DEF=S△DGH，
∵△ADG和△AED的面积分别为51和38，
∴△EDF的面积=．
故选A．
本题考查的知识点是角平分线的性质及全等三角形的判定及性质，解题关键是正确地作出辅助线，将所求的三角形的面积转化为另外的三角形的面积来求．
6、C
【解析】
结合题意分情况讨论：①当点P在AE上时，②当点P在AD上时，③当点P在DC上时，根据三角形面积公式即可得出每段的y与x的函数表达式.
【详解】
①当点在上时，
∵正方形边长为4，为中点，
∴，
∵点经过的路径长为，
∴，
∴，
②当点在上时，
∵正方形边长为4，为中点，
∴，
∵点经过的路径长为，
∴，，
∴，
，
，
，
③当点在上时，
∵正方形边长为4，为中点，
∴，
∵点经过的路径长为，
∴，，
∴，
综上所述：与的函数表达式为：
.
故答案为：C.
本题考查动点问题的函数图象，解决动点问题的函数图象问题关键是发现y随x的变化而变化的趋势．
7、D
【解析】
由于直角三角形的斜边不能确定，故应分5是直角边或5是斜边两种情况进行讨论．
【详解】
当5是直角边时，则第三边=；
当5是斜边时，则第三边=．
综上所述，第三边的长是或1．
故选D．
本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
8、A
【解析】
根据平行四边形的性质推出OA=OC=AC，OB=OD=BD，求出每个选项中OA和OB的值，再判断OA、OB、AD的值是否能组成三角形即可．
【详解】
解：∵四边形ABCD是平行四边形，∴OA=OC=AC，OB=OD=BD，
A、∵AC=10，BD=12，∴OA=5，OD=6，∵6-5＜10＜6+5，∴此时能组成三角形，故本选项符合题意；
B、∵AC=12，BD=32，∴OA=6，OD=16，∵16-6=10，∴此时不能组成三角形，故本选项不符合题意；
C、∵AC=6，BD=8，∴OA=3，OD=4，∵3+4＜10，∴此时不能组成三角形，故本选项不符合题意；
D、∵AC=8，BD=10，∴OA=4，OD=5，∵4+5＜10，∴此时不能组成三角形，故本选项不符合题意；
故选：A．
本题考查了三角形的三边关系定理和平行四边形的性质，关键是判断OA、OB、AD的值是否符合三角形的三边关系定理．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、5cm
【解析】
根据角平分线的性质、RT△中，30°所对的直角边等于斜边的一般，本题得以解决．
【详解】
解：由题意可得，
OC为∠MON的角平分线，
∵，OC平分∠AOB，∴∠MOP=∠MON=30°,
∵，∴∠ODP=90°,
∵OP=10，
∴PD=OP=5，
故答案为：5cm．
本题考查了角平分线的性质及直角三角形的性质，解题的关键是掌握直角三角形的性质．
10、 (－1，－1)
【解析】
根据菱形的性质，可得D点坐标，根据旋转的性质，可得D点的坐标．
【详解】
菱形OABC的顶点O（0，0），B（2，2），得
D点坐标为（1，1）．
每秒旋转45°，则第60秒时，得
45°×60=2700°，
2700°÷360=7.5周，
OD旋转了7周半，菱形的对角线交点D的坐标为（-1，-1），
故答案为：（-1，-1）．
本题考查了旋转的性质，利用旋转的性质是解题关键．
11、1
【解析】
根据三角形中位线定理求出DE，根据直角三角形的性质求出EF，结合图形计算即可．
【详解】
∵DE为△ABC的中位线，
∴DE=BC=4(cm)，
∵∠AFC为直角，E为AC的中点，
∴FE=AC=3(cm)，
∴DF=DE−FE=1(cm)，
故答案为：1cm.
此题考查三角形中位线定理，解题关键在于掌握其性质定义.
12、4
【解析】
按照二次根式的乘、除运算法则运算即可求解.
【详解】
解：原式=
故答案为：4.
本题考查二次根式的乘除运算法则，熟练掌握运算公式是解决此类题的关键.
13、3＜x＜1
【解析】
满足不等式组0＜kx+b＜x就是一次函数的图象位于正比例函数的图象的下方且位于x轴的上方部分x的取值范围，据此求解．
【详解】
解：∵与直线y=x交于点A，点B的坐标为（1，0），
∴不等式组0＜kx+b＜x的解集为3＜x＜1．
故答案为3＜x＜1.
本题考查了一次函数与一元一次不等式的问题，满足不等式组0＜kx+b＜x就是一次函数的图象位于正比例函数的图象的下方且位于x轴的上方时x的取值范围是解答本题的关键．
三、解答题（本大题共5个小题，共48分）
14、（1）900；（2）当两车出发4小时时相遇；（3）慢车的速度是75千米/时，快车的速度是150千米/时；（4）y=225x﹣900（4≤x≤6）．
【解析】
（1）根据已知条件和函数图象可以直接写出甲、乙两地之间的距离；
（2）根据题意可以得到点B表示的实际意义；
（3）根据图象和题意可以分别求出慢车和快车的速度；
（4）根据题意可以求得点C的坐标，由图象可以得到点B的坐标，从而可以得到线段BC所表示的y与x之间的函数关系式，以及自变量x的取值范围．
【详解】
（1）由图象可得：甲、乙两地之间的距离为900千米．
故答案为900；
（2）图中点B的实际意义时当两车出发4小时时相遇；
（3）由题意可得：慢车的速度为：900÷12=75，快车的速度为：（900﹣75×4）÷4=150，即慢车的速度是75千米/时，快车的速度是150千米/时；
（4）由题可得：点C是快车刚到达乙地，∴点C的横坐标是：900÷150=6，纵坐标是：900﹣75×6=450，即点C的坐标为（6，450），设线段BC对应的函数解析式为y=kx+b．
∵点B（4，0），点C（6，450），∴，得：，即线段BC所表示的y与x之间的函数关系式是y=225x﹣900（4≤x≤6）．
本题考查了一次函数的应用，解答此类问题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答，注意最后要写出自变量x的取值范围．
15、（1）；；；（2）选甲队好
【解析】
（1）根据中位数定义，众数的的定义方差的计算公式代值计算即可；
（2）根据方差的意义即可得出答案．
【详解】
解：（1）根据图象可知道乙队一个10人，中位数在第五六位之间，故为；
估计表中数据178出现了4次，出现的次数最多，所以；根据方差公式即可计算出
故答案为：；；.
（2）选甲队好.
∵甲队的方差为0.6，乙队的方差为1.8.
∴甲队的方差小于乙队的方差.
∴甲队的身高比乙队整齐. .
∴选甲队比较好.
此题考查方差，加权平均数，中位数，众数，解题关键在于看懂图中数据
16、（1）；（2）①1；②
【解析】
（1）先利用直线y=3x+3确定A、B的解析式，然后利用一次函数的性质求解；
（2））①把C（-，n）代入y=3x+3可求出n的值；
②利用两直线垂直，一次项系数互为负倒数可设直线CD的解析式为y=-x+b，然后把C（-，1）代入求出b即可．
【详解】
解：（1）当y=0时，3x+3=0，解得x=-1，则A（-1，0），
当x=0时，y=3x+3=3，则B（0，3），
当0＜y≤3，自变量x的取值范围是-1≤x＜0；
（2）①把C（-，n）代入y=3x+3得3×（-）+3=n，解得n=1；
②∵AB⊥CD，
∴设直线CD的解析式为y=-x+b，
把C（-，1）代入得-×（-）+b=1，解得b=，
∴直线CD的解析式为y=-x+．
本题考查了待定系数法求一次函数解析式：先设出函数的一般形式，如求一次函数的解析式时，先设y=kx+b；将自变量x的值及与它对应的函数值y的值代入所设的解析式，得到关于待定系数的方程或方程组；解方程或方程组，求出待定系数的值，进而写出函数解析式．也考查了一次函数的性质．
17、（1）m＝100（2）两种方案
【解析】
（1）用总价除以单价表示出购进童装的数量，根据两种童装的数量相等列出方程求解即可；
（2）设购进甲种童装x件，表示出乙种童装（200-x）件，然后根据总利润列出一元一次不等式，求出不等式组的解集后，再根据童装的件数是正整数解答；设总利润为W，表示出利润，求得最值即可．
【详解】
（1）根据题意可得：，
解得：m＝100，
经检验m＝100是原方程的解；
（2）设甲种童装为x件，可得：，
解得：98≤x＜100，
因为x取整数，
所以有两种方案：
方案一：甲98，乙102；
方案二：甲99，乙101；
本题考查了分式方程的应用，一元一次不等式组的应用，解决问题的关键是读懂题意，找到关键描述语，进而找到所求的量的等量关系和不等关系，解决问题．
18、（1）详见解析；（2）70~80或“举人”；（3）231.
【解析】
（1）先根据90～100分的人数及其所占百分比求得总人数，再由各组人数之和等于总人数求得60～70分的人数．从而补全图形；
（2）根据中位数的定义求解可得；
（3）利用样本估计总体的思想求解可得．
【详解】
解：（1）∵被调查的总人数为6÷12.5%=48（人），
∴60～70分的人数为48-（3+18+9+6）=12（人），
补全频数分布直方图如下：
（2）因为中位数是第24、25个数据的平均数，而第24、25个数据都落在70～80分这一组，
所以在此次比赛中，抽取学生的成绩的中位数在70~80或“举人”组，
故答案为70~80或“举人”；
（3）．
答：大约有231名学生获奖．
故答案为（1）详见解析；（2）70~80或“举人”；（3）231.
本题考查频数分布表、频数分布直方图，解题的关键是明确题意，找出所求问题需要的条件，利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、1
【解析】
直接利用二次根式有意义的条件得出a的值，进而利用负指数幂的性质得出答案．
【详解】
解：∵b＝+﹣2，
∴
∴1-2a=0，
解得：a=，则b=-2，
故ab=（）-2=1．
故答案为1．
此题主要考查了二次根式有意义的条件，以及负指数幂的性质，正确得出a的值是解题关键．
20、四
【解析】
根据根与系数的关系可得出a＋b＝1、ab＝4，再结合一次函数图象与系数的关系，即可得出一次函数y＝abx＋a＋b的图象经过的象限，此题得解．
【详解】
解：∵一元二次方程的两个实数根分别是a、b，
∴a＋b＝1，ab＝4，
∴一次函数的解析式为y＝4x＋1．
∵4＞0，1＞0，
∴一次函数y＝abx＋a＋b的图象经过第一、二、三象限，不经过第四象限，
故答案为：四.
本题考查了根与系数的关系以及一次函数图象与系数的关系，利用根与系数的关系结合一次函数图象与系数的关系，找出一次函数图象经过的象限是解题的关键．
21、
【解析】
设直线的解析式为y=kx+b(k≠0)，
∵A(1,1)，B(4,0)，
，解之得 ，
∴直线AB的解析式为 ，
∵P(2,m)在直线上，
.
22、±2
【解析】
先根据新定义得出一元二次方程，求出方程的解即可．
【详解】
解：由题意可得：x+1-（x+1）•x=-3，
-x2=-4，
解得：x=±2，
故答案为：±2
本题考查了解一元二次方程的应用，解此题的关键是能根据已知得出一元二次方程，题目比较新颖，难度适中．
23、x=3
【解析】
先将-x移到方程右边，再把方程两边平方，使原方程化为整式方程x2=9，求出x的值，把不合题意的解舍去，即可得出原方程的解.
【详解】
解：整理得：=x+1，
方程两边平方，得：2x+10=x2+2x+1，
移项合并同类项，得：x2=9，
解得：x1=3，x2=-3，
经检验，x2=-3不是原方程的解，
则原方程的根为：x=3.
故答案为：x=3.
本题考查了解无理方程，无理方程在有些地方初中教材中不再出现，比如湘教版.
二、解答题（本大题共3个小题，共30分）
24、, .
【解析】
根据分式的运算法则即可求出答案．
【详解】
解：原式==.
当x=+1时，
原式==.
点睛：本题考查分式的运算，解题的关键是熟练运用分式的运算法则，本题属于基础题型．
25、12
【解析】
在Rt△ABC中，∠C＝90°，AC＝5，AB＝13，根据勾股定理，即可求出BC．
【详解】
解：∵在Rt△ABC中，∠C＝90°，
∴
∴
∴
又∵AC＝5，AB＝13，
∴
=
=12
此题主要考查勾股定理的运用.
26、 (1) y=x；
(2) m=.
【解析】
（1）设y+3=k（5x+4），把x=1，y=-18代入求出k的值，进而可得出y与x的函数关系式；
（2）直接把点（m，-8）代入（1）中一次函数的解析式即可．
【详解】
(1)∵y+3与5x+4成正比例，
∴设y+3=k(5x+4)，
∵当x=1时，y=−18，
∴−18+3=k(5+4),解得k=，
∴y关于x的函数关系式为： (5x+4)=y+3,即y=x；
(2)∵点(m,−8)在此图象上，
∴−8=m,解得m=.
本题考查一次函数，解题的关键是掌握待定系数法求解析式.
题号
一
二
三
四
五
总分
得分
甲
乙
丙
丁
平均数（cm）
185
180
185
180
方差
3.6
3.6
7.4
8.1
甲队
178
177
179
179
178
178
177
178
177
179
平均数
中位数
众数
方差
甲队
178
178
b
0.6
乙队
178
a
178
c
价格
甲
乙
进价（元/件）
m
m+20
售价（元/件）
150
160