

所属成套资源:2024-2025学年高考数学一轮复习讲义(新高考)(分层精练)(学生版+解析)
- 2024-2025学年高考数学一轮复习讲义(新高考)第02讲等差数列及其前n项和(含新定义解答题)(分层精练)(学生版+解析) 试卷 0 次下载
- 2024-2025学年高考数学一轮复习讲义(新高考)第02讲等差数列及其前n项和(知识+真题+6类高频考点)(精讲)(学生版+解析) 试卷 0 次下载
- 2024-2025学年高考数学一轮复习讲义(新高考)第03讲两角和与差的正弦、余弦和正切公式(知识+真题+6类高频考点)(精讲)(学生版+解析) 试卷 0 次下载
- 2024-2025学年高考数学一轮复习讲义(新高考)第03讲函数的奇偶性、对称性与周期性(含新定义解答题)(分层精练)(学生版+解析) 试卷 0 次下载
- 2024-2025学年高考数学一轮复习讲义(新高考)第03讲函数的奇偶性、对称性与周期性(知识+真题+10类高频考点)(精讲)(学生版+解析) 试卷 0 次下载
2024-2025学年高考数学一轮复习讲义(新高考)第03讲两角和与差的正弦、余弦和正切公式(含新定义解答题)(分层精练)(学生版+解析)
展开
这是一份2024-2025学年高考数学一轮复习讲义(新高考)第03讲两角和与差的正弦、余弦和正切公式(含新定义解答题)(分层精练)(学生版+解析),共14页。试卷主要包含了已知,且,求的值;,已知,,且.等内容,欢迎下载使用。
A.B.C.D.
二、多选题
9.(23-24高一下·湖南岳阳·阶段练习)计算下列各式,结果为的是( )
A.B.C.D.
10.(23-24高一下·江苏常州·阶段练习)下列化简结果正确的是( )
A.B.
C.D.
三、填空题
11.(23-24高一下·上海·阶段练习)已知,且,则 .
12.(2024高三·全国·专题练习)已知tan α=-,cs β=,α∈(,π),β∈(0,),则α+β= .
四、解答题
13.(23-24高一下·上海·阶段练习)(1)已知,且,求的值;
(2)已知,求的值.
14.(2024高一下·上海·专题练习)已知,,且.
(1)求的值;
(2)求的值.
B能力提升
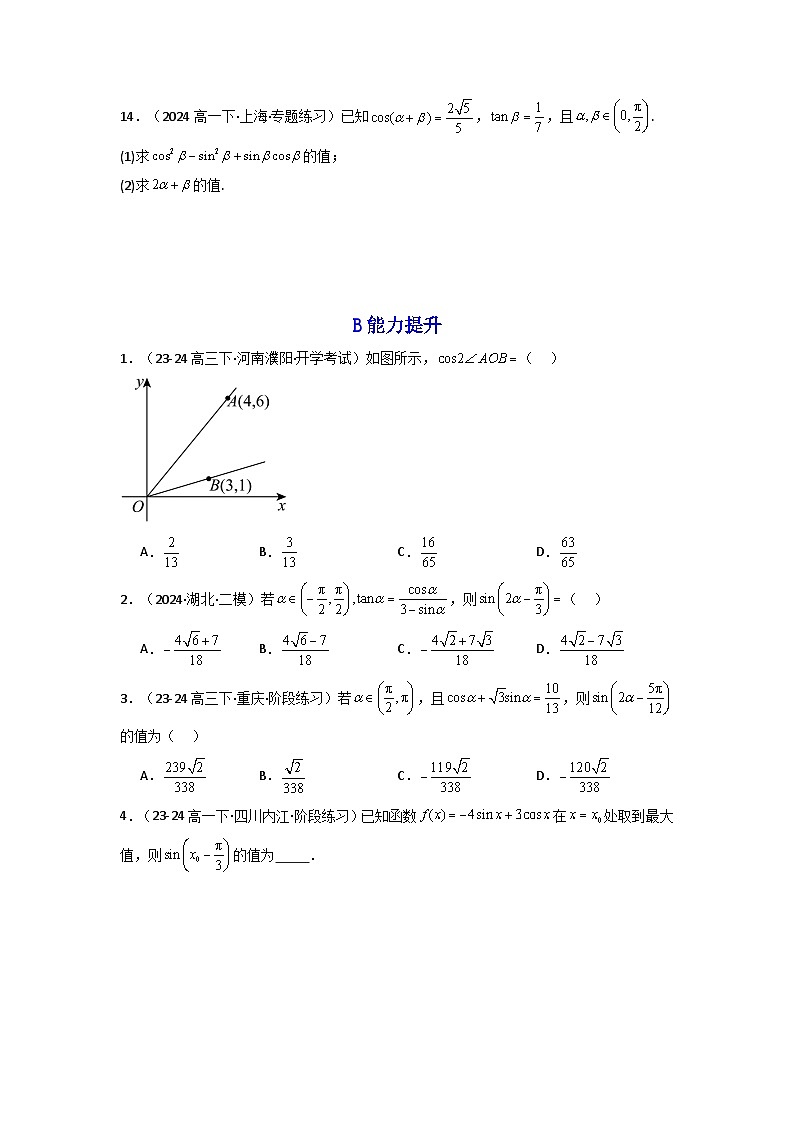
1.(23-24高三下·河南濮阳·开学考试)如图所示,( )
A.B.C.D.
2.(2024·湖北·二模)若,则( )
A.B.C.D.
3.(23-24高三下·重庆·阶段练习)若,且,则的值为( )
A.B.C.D.
4.(23-24高一下·四川内江·阶段练习)已知函数在处取到最大值,则的值为 .
5.(2024高一下·全国·专题练习)圭表是我国古代一种通过测量正午日影长度来推定节气的天文仪器,它包括一根呈南北方向的水平长尺(称为“圭”)和一根直立于圭面的标杆(称为“表”),如图.成语有云:“立竿见影”,《周髀算经》里记载的二十四节气就是通过圭表测量日影长度来确定的.利用圭表测得某市在每年夏至日的早上8:00和中午13:00的太阳高度角分别为()和().设表高为1米,则影差 米(参考数据:,)
C综合素养(新定义解答题)
1.(23-24高一下·广东江门·阶段练习)在数学中,双曲函数是与三角函数类似的函数,最基本的双曲函数是双曲正弦函数与双曲余弦函数,其中双曲正弦函数:,双曲余弦函数:.(e是自然对数的底数,).双曲函数的定义域是实数集,其自变量的值叫做双曲角,双曲函数出现于某些重要的线性微分方程的解中,譬如说定义悬链线和拉普拉斯方程.
(1)计算的值;
(2)类比两角和的余弦公式,写出两角和的双曲余弦公式:______,并加以证明;
(3)若对任意,关于的方程有解,求实数的取值范围.
第03讲 两角和与差的正弦、余弦和正切公式 (分层精练)
A夯实基础B能力提升C综合素养(新定义解答题)
A夯实基础
一、单选题
1.(23-24高一下·广东佛山·阶段练习)( )
A.B.C.D.
【答案】B
【分析】逆用正切的和差公式,结合特殊角的三角函数值即可得解.
【详解】.
故选:B.
2.(23-24高一下·江苏连云港·阶段练习)( )
A.B.C.D.
【答案】B
【分析】
根据正弦的差角公式即可化简求解.
【详解】,
故选:B
3.(22-23高一下·江苏苏州·期末)( )
A.B.C.D.
【答案】C
【分析】
由两角差的余弦公式逆用即可求解.
【详解】由题意.
故选:C.
4.(23-24高一上·浙江台州·期末)已知,,则( )
A.B.C.D.
【答案】A
【分析】
,利用两角和的正切公式求解.
【详解】已知,,
则.
故选:A
5.(23-24高一上·广东深圳·期末)如图,有三个相同的正方形相接,若,,则( )
A.B.
C.D.
【答案】B
【分析】
设正方体边长为1,由图可得,结合两角和的正切公式计算即可求解.
【详解】
设正方体边长为1,由图可得,
则且,
所以.
故选:B.
6.(2024·四川南充·二模)已知函数.设时,取得最大值.则( )
A.B.C.D.
【答案】C
【分析】利用辅助角公式求出,再利用诱导公式以及正弦的和差角公式可得答案.
【详解】,其中;
所以当时,,取得最大值,
由题意,即.
.
故选:C
7.(23-24高一下·四川资阳·阶段练习)已知都是锐角,,则为( )
A.B.C.D.
【答案】C
【分析】要求,先求,结合已知可有,利用两角差的余弦公式展开可求.
【详解】、为锐角,
,
,
由于为锐角,.
故选:C
8.(21-22高三上·湖南株洲·期中)在平面直角坐标系中,角与的顶点均为坐标原点O,始边均为x轴的非负半轴.若角的终边与单位圆交于点,将OP绕原点O按逆时针方向旋转后与角的终边重合,则( )
A.B.C.D.
【答案】A
【分析】
由题意利用任意角的三角函数的定义求得,,再利用两角和的余弦公式求解.
【详解】
由题意可得,,
由于,所以.
故选:A.
二、多选题
9.(23-24高一下·湖南岳阳·阶段练习)计算下列各式,结果为的是( )
A.B.C.D.
【答案】BC
【分析】运用二倍角公式、和差角公式的逆用、特殊角的三角函数值、三角恒等变换中“1”的代换化简即可.
【详解】对于选项A,,故选项A错误;
对于选项B,,故选项B正确;
对于选项C,,故选项C正确;
对于选项D,,故选项D错误.
故选:BC.
10.(23-24高一下·江苏常州·阶段练习)下列化简结果正确的是( )
A.B.
C.D.
【答案】BCD
【分析】
利用和(差)角公式计算可得.
【详解】对于A:,故A错误;
对于B:,故B正确;
对于C:
,故C正确;
对于D:
,故D正确.
故选:BCD
三、填空题
11.(23-24高一下·上海·阶段练习)已知,且,则 .
【答案】
【分析】根据题意利用两角和差公式分析求解.
【详解】因为,
由题意可得,即,
且,可知.
故答案为:.
12.(2024高三·全国·专题练习)已知tan α=-,cs β=,α∈(,π),β∈(0,),则α+β= .
【答案】
【详解】
由cs β=,β∈(0,),得sin β=,tan β=2,
所以tan (α+β)===1.
因为α∈(,π),β∈(0,),所以<α+β<,
所以α+β=.
四、解答题
13.(23-24高一下·上海·阶段练习)(1)已知,且,求的值;
(2)已知,求的值.
【答案】(1)7;(2)
【分析】
(1)利用同角三角函数之间的基本关系可求得,再由两角差的正切公式可得结果;
(2)根据与的关系式判断出,即可得结果.
【详解】(1),且,可得
所以
(2)由
两边平方可得:即,
所以,则,
因此
.
14.(2024高一下·上海·专题练习)已知,,且.
(1)求的值;
(2)求的值.
【答案】(1)
(2)
【分析】
(1)利用平方关系将式子化成齐次式,再将弦化切,最后代入计算可得;
(2)首先由同角三角函数的基本关系求出,,,由二倍角公式求出、,最后由并利用两角差的余弦公式计算可得.
【详解】(1)
因为,
所以
;
(2)
且,
,则,
,
,
,,且,解得(负值舍去),
,
又,,,
.
B能力提升
1.(23-24高三下·河南濮阳·开学考试)如图所示,( )
A.B.C.D.
【答案】C
【分析】由题意求出的正弦值以及余弦值,根据两角差的余弦公式求得,再由二倍角余弦公式,即可求得答案.
【详解】由题意知,
则,,
故
,
故,
故选:C
2.(2024·湖北·二模)若,则( )
A.B.C.D.
【答案】D
【分析】首先根据公式化解条件等式,再结合二倍角和两角差的正弦公式,即可化解求值.
【详解】由条件等式可知,,
值,则的值为 .
【答案】
【分析】利用两角和的余弦公式将函数化简得到其中,再由余弦函数的性质及两角差的正弦公式计算可得.
【详解】因为,其中,
又函数在处取到最大值,
所以,
不妨令,则,
所以
.
故答案为:
5.(2024高一下·全国·专题练习)圭表是我国古代一种通过测量正午日影长度来推定节气的天文仪器,它包括一根呈南北方向的水平长尺(称为“圭”)和一根直立于圭面的标杆(称为“表”),如图.成语有云:“立竿见影”,《周髀算经》里记载的二十四节气就是通过圭表测量日影长度来确定的.利用圭表测得某市在每年夏至日的早上8:00和中午13:00的太阳高度角分别为()和().设表高为1米,则影差 米(参考数据:,)
【答案】2.232
【分析】
由正弦定理和三角函数得到,利用正弦和差公式得到,求出(米).
【详解】
在中,(米).
在中,由正弦定理,得,
即,
所以(米).
因为,
且,
所以,所以(米).
故答案为:
C综合素养(新定义解答题)
1.(23-24高一下·广东江门·阶段练习)在数学中,双曲函数是与三角函数类似的函数,最基本的双曲函数是双曲正弦函数与双曲余弦函数,其中双曲正弦函数:,双曲余弦函数:.(e是自然对数的底数,).双曲函数的定义域是实数集,其自变量的值叫做双曲角,双曲函数出现于某些重要的线性微分方程的解中,譬如说定义悬链线和拉普拉斯方程.
(1)计算的值;
(2)类比两角和的余弦公式,写出两角和的双曲余弦公式:______,并加以证明;
(3)若对任意,关于的方程有解,求实数的取值范围.
【答案】(1)
(2),证明见解析
(3)
【分析】(1)根据新定义函数直接计算即可;
(2)类比可得,根据新函数定义计算即可证明;
(3)由可得,分离参数,求出,即可得解.
【详解】(1)由已知可得,,,
所以,
所以.
(2),证明如下:
左边,
右边
.
所以,左边=右边,
所以.
(3)原题可转化为方程有解,即有解.
令,,,
因为在上单调递增,,,
所以.
又,当且仅当,即时等号成立,
所以,即,即,
所以,即.
相关试卷
这是一份2024-2025学年高考数学一轮复习讲义(新高考)第03讲等比数列及其前n项和(含新定义解答题)(分层精练)(学生版+解析),共13页。试卷主要包含了在数列中,已知,等内容,欢迎下载使用。
这是一份2024-2025学年高考数学一轮复习讲义(新高考)第03讲平面向量的数量积(含新定义解答题)(分层精练)(学生版+解析),共15页。试卷主要包含了已知,.,在四边形中,已知,,.,,且,设等内容,欢迎下载使用。
这是一份2024-2025学年高考数学一轮复习讲义(新高考)第03讲导数与函数的极值、最值(含新定义解答题)(分层精练)(学生版+解析),共18页。试卷主要包含了已知函数,则下列说法正确的有,已知函数.等内容,欢迎下载使用。








