2024-2025学年安徽省阜阳市太和中学高二上学期10月月考数学试题（含答案）

这是一份2024-2025学年安徽省阜阳市太和中学高二上学期10月月考数学试题（含答案），共8页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。

1.已知集合{x|13x2+x<0},B={−2,0,2,3}，则A∩B=( )
A. {−2,0}B. {2}C. {−2}D. {2,3}
2.若直线x2+y7=1的倾斜角为θ，则tanθ=( )
A. −27B. −72C. 27D. 72
3.第33届夏季奥林匹克运动会于2024年7月26日至8月11日在法国巴黎举行，金牌榜前10名的国家的金牌数依次为40，40，20，18，16，15，14，13，12，12，则这10个数的60%分位数是( )
A. 14.5B. 15C. 16D. 17
4.在空间直角坐标系Oxyz中，已知点A(2,−1,1)，B(1,1,2)，若点C与点B关于平面xOz对称，则|AC|=( )
A. 2B. 6C. 14D. 22
5.若ab<0，bc>0，在同一平面直角坐标系中作出直线ax−by+b=0与直线bx−cy−b=0，则下列图中能表示上述两条直线的位置的是( )
A. B.
C. D.
6.已知△ABC中，内角A，B，C所对的边分别为a，b，c，若a=2b，c= 6，则当B取得最大值时，△ABC的面积为( )
A. 3B. 3C. 2 3D. 6
7.已知甲、乙两人进行扳手腕游戏，且每人各有2个乒乓球.每次扳手腕甲获胜的概率均为23，没有平局，且每次扳手腕的结果互不影响.每次负方给胜方1个乒乓球，直到一方没有乒乓球时游戏结束，则第1次甲胜且第4次扳手腕后游戏结束的概率为( )
A. 1027B. 29C. 1681D. 1081
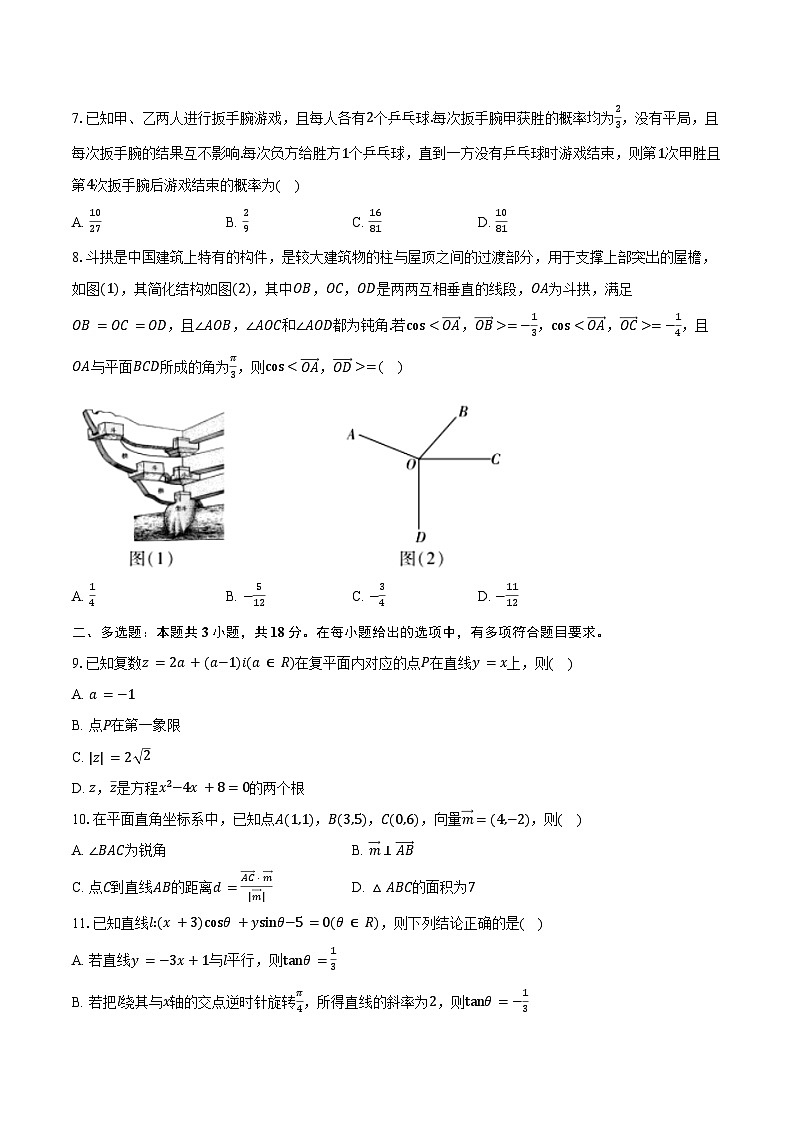
8.斗拱是中国建筑上特有的构件，是较大建筑物的柱与屋顶之间的过渡部分，用于支撑上部突出的屋檐，如图(1)，其简化结构如图(2)，其中OB，OC，OD是两两互相垂直的线段，OA为斗拱，满足OB=OC=OD，且∠AOB，∠AOC和∠AOD都为钝角.若cs=−13，cs=−14，且OA与平面BCD所成的角为π3，则cs=( )
A. 14B. −512C. −34D. −1112
二、多选题：本题共3小题，共18分。在每小题给出的选项中，有多项符合题目要求。
9.已知复数z=2a+(a−1)i(a∈R)在复平面内对应的点P在直线y=x上，则( )
A. a=−1
B. 点P在第一象限
C. |z|=2 2
D. z，z是方程x2−4x+8=0的两个根
10.在平面直角坐标系中，已知点A(1,1)，B(3,5)，C(0,6)，向量m=(4,−2)，则( )
A. ∠BAC为锐角B. m⊥AB
C. 点C到直线AB的距离d=AC⋅m|m|D. △ABC的面积为7
11.已知直线l:(x+3)csθ+ysinθ−5=0(θ∈R)，则下列结论正确的是( )
A. 若直线y=−3x+1与l平行，则tanθ=13
B. 若把l绕其与x轴的交点逆时针旋转π4，所得直线的斜率为2，则tanθ=−13
C. 若θ∈(0,π2)，l与直线y=2x−6及两坐标轴的正半轴围成的四边形有外接圆，则sinθ= 55
D. 对任意的θ，都存在定点P，使得点P到l的距离为定值
三、填空题：本题共3小题，每小题5分，共15分。
12.计算：lg419+16810.25−lg438= ．
13.若点P(m,n)为直线x−2y−8=0上的动点，则 m2+(n−1)2的最小值为 ．
14.已知在空间直角坐标系Oxyz中，过点P(x1,y1,z1)且一个法向量为n=(x2,y2,z2)的平面α的方程为x2(x−x1)+y2(y−y1)+z2(z−z1)=0.若平面α的方程为3x−y+2z=0，直线l的一个方向向量为a=(2,1,3)，则直线l与平面α所成角的正弦值为 ．
四、解答题：本题共5小题，共60分。解答应写出文字说明，证明过程或演算步骤。
15.(本小题12分)
已知点P(−2,−3)，点O为坐标原点．
(Ⅰ)若直线l过点(0,2)，且OP//l，求l的方程;
(Ⅱ)若直线l过点P，与x轴负半轴及y轴负半轴分别交于点A，B，且|OA|=23|OB|，求|PA||PB|的值．
16.(本小题12分)
如图，正四棱柱ABCD−A1B1C1D1的底面边长为2，E为棱CD的中点，FC1=3CF，且四棱锥E−BCFB1的体积为5 26．
(Ⅰ)求棱CC1的长;
(Ⅱ)证明：平面BCD1⊥平面B1EF．
17.(本小题12分)
已知在△ABC中，点A(−1,0)，角C的平分线所在直线的方程为y=x+2，AB边上的高所在直线的方程为x+2y−7=0．
(Ⅰ)求点C的坐标及直线AB的方程;
(Ⅱ)求点B的坐标．
18.(本小题12分)
如图，在六棱柱ABCDEF−A1B1C1D1E1F1中，底面ABCDEF是正六边形，设AB=a，AF=b，AA1=c．
(Ⅰ)用a，b，c分别表示A1D，A1C．
(Ⅱ)若cs∠BAA1=cs∠FAA1=14，AB=2，AA1=4，求：
(ⅰ)A1C⋅A1D;
(ⅱ)|AE1|.
19.(本小题12分)
若函数f(x)的图象上存在两个不同的点Ai(xi,yi)(i=1,2)，使得对任意x∈R，都有f(2xi−x)+f(x)=2yi，则称f(x)为类周期函数．
(Ⅰ)证明：f(x)=x+sinx是类周期函数;
(Ⅱ)若f(x)是类周期函数，且x1=−1，x2=3，y1=y2，证明：f(x)是周期函数;
(Ⅲ)若f(x)是类周期函数，证明：在f(x)的图象上，必存在3个不同的点Ai(xi,yi)(i=1,2,3)，使得对任意x∈R，都有f(2xi−x) +f(x) =2yi．
参考答案
1.C
2.B
3.D
4.A
5.C
6.A
7.D
8.D
9.AC
10.ABD
11.AD
12.16
13.2 5
14.1114
15.解：(Ⅰ)由P(−2,−3)得直线OP的斜率k=−3−2=32，
因为OP//l，所以l的斜率为32．
又l过点(0,2)，
故l的方程为y−2=32(x−0)，即3x−2y+4=0．
(Ⅱ)因为l与x轴负半轴及y轴负半轴分别交于点A，B，且|OA|=23|OB|，
所以可设A(2a,0)，B(0,3a)(a<0)，
由截距式方程可得l的方程为x2a+y3a=1，
把(−2,−3)代入上式，可得a=−2，所以A(−4,0)，B(0,−6)，
所以|PA||PB|= (−4+2)2+(0+3)2 (0+2)2+(−6+3)2=1．
16.解：(I)由题意可知EC⊥平面BCFB1，四边形BCFB1是直角梯形，设CC1=ℎ，
所以V=13×EC×12(FC+BB1)×BC=13×1×12×(ℎ4+ℎ)×2=5 26，
解得ℎ=2 2，即CC1=2 2．
(Ⅱ)以点D为原点，直线DA，DC，DD1分别为x轴、y轴、z轴建立如图所示的空间直角坐标系．
由题意得C(0,2,0)，B(2,2,0)，D1(0,0,2 2)，E(0,1,0)，F(0,2, 22)，B1(2,2,2 2)，
所以CB=(2,0,0)，CD1=(0,−2,2 2)，EF=(0,1, 22,FB1=(2,0,3 22)，
设平面BCD1的法向量为n1=(x1,y1,z1)，则n1⋅CB=0,n1⋅CD1=0,即2x1=0,−2y1+2 2z1=0,
取z1=1，得n1=(0, 2,1)，
设平面B1EF的法向量为n2=(x2,y2,x2)，则n2⋅EF=0,n2⋅FB1=0,即y2+ 22z2=02x2+3 22z2=0,
取z2=2，得n2=(−3 22,− 2,2)
因为n1⋅n2=−2+2=0，所以平面BCD1⊥平面B1EF．
17.解：(I)由题可知，点C是直线y=x+2与直线x+2y−7=0的交点，联立x−y+2=0,x+2y−7=0,解得x=1,y=3,所以点C的坐标为(1,3)．
设直线AB的斜率为k，因为直线AB与直线x+2y−7=0垂直，所以k×(−12)=−1，解得k=2，
又点A的坐标为(−1,0)，所以直线AB的方程为y−0=2(x+1)，即2x−y+2=0．
(Ⅱ)设点A关于直线y=x+2对称的点为A′(m,n).因为直线y=x+2为角C的平分线，所以A′在直线BC上，
由nm+1=−1,m−12−n2+2=0,解得m=−2,n=1,所以直线BC的斜率为1−3−2−1=23，则直线BC的方程为y−3=23(x−1)，即2x−3y+7=0．
联立直线AB与直线BC的方程，得2x−y+2=0,2x−3y+7=0,解得x=14,y=52,所以点B的坐标为(14,52)
18.解：(I)如图，连接AD，
因为六边形ABCDEF是正六边形，所以AB+AF=12AD，则AD=2a+2b
所以A1D=AD−AA1=2a+2b−c，A1C=A1D+DC=A1D−AF=2a+b−c．
(Ⅱ)因为六边形ABCDEF是正六边形，所以∠BAF=2π3，又cs∠BAA1=cs∠FAA1=14，AB=2，AA1=4，
所以|a|=1，|b|=2，|c|=4，a⋅b=|a||b|cs2π3=−2，a⋅c=b⋅c=|a||c|×14=2．
(i)A1C⋅A1D=(2a+b−c)⋅(2a+2b−c)=4a2+2b2+c2+6a⋅b−3b⋅c−4a⋅c=16+8+16−12−6−8=14．
(ii)因为AE1=AD+DE+EE1=AD−AB+AA1=2a+2b−a+c=a+2b+c，
所以|AE1|= (a+2b+c)2= a2+4b2+c2+4a⋅b+4b⋅c+2a⋅c= 4+16+16−8+8+4=2 10．
19.解：(Ⅰ)假设f(x)=x+sinx是类周期函数，
则2xi−x+sin(2xi−x)+x+sinx=2xi+2sinxi(i=1,2)，
整理得sin(2xi−x)+sinx=2sinxi，
即(1−cs2xi)sinx+sin2xicsx=2sinxi，
所以1−cs 2xi=0,sin 2xi=0,2sinxi=0,则当x1=0，x2=π时满足条件，
所以f(x)=x+sinx是类周期函数．
(Ⅱ)由题意得f(−2−x)+f(x)=2y1，f(6−x)+f(x)=2y1，
两式相减得f(6−x)=f(−2−x)，
用−x−2代换上式中的x，得f(x+8)=f(x)，
所以f(x)是周期为8的周期函数．
(Ⅲ)因为f(x)是类周期函数，
所以f(x)的图象上存在两个不同的点Ai(xi,yi)(i=1,2)，使得对任意x∈R，都有f(2xi−x)+f(x)=2yi，
由f(2x1−x)+f(x)=2y1，得f(2x1−2x2+x)+f(2x2−x)=2y1， ①
由f(2x2−x)+f(x)=2y2，得f(4x2−2x1−x)+f(2x1−2x2+x)=2y2， ②
②− ①，得f(4x2−2x1−x)−f(2x2−x)=2y2−2y1，
即f(4x2−2x1−x)−[2y2−f(x)]=2y2−2y1，
所以f(4x2−2x1−x)+f(x)=4y2−2y1，
令x=2x2−x1，得f(2x2−x1)=2y2−y1，
所以点(2x2−x1,2y2−y1)在f(x)的图象上，且f(x)的图象关于点(2x2−x1,2y2−y1)中心对称，
因为x1≠x2，所以2x2−x1≠x1，2x2−x1≠x2，
取x3=2x2−x1，y3=2y2−y1，则f(2x3−x)+f(x)=2y3，
所以必存在3个不同的点Ai(xi,yi)(i=1,2,3)，使得对任意x∈R，都有f(2xi−x)+f(x)=2yi．