江苏省无锡市宜兴市桃溪中学2024年九年级数学第一学期开学经典模拟试题【含答案】

这是一份江苏省无锡市宜兴市桃溪中学2024年九年级数学第一学期开学经典模拟试题【含答案】，共25页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）甲、乙两车从A地出发，沿同一路线驶向B地．甲车先出发匀速驶向B地，40min后，乙车出发，匀速行驶一段时间后，在途中的货站装货耗时半小时．由于满载货物，为了行驶安全，速度减少了50km/h，结果与甲车同时到达B地．甲乙两车距A地的路程y（km）与乙车行驶时间x（h）之间的函数图象如图所示，则下列说法中正确的有（ ）
①；②甲的速度是60km/h；③乙出发80min追上甲；④乙刚到达货站时，甲距B地180km．
A．4个B．3个C．2个D．1个
2、（4分）如图，A、B两地被池塘隔开，小康通过下列方法测出了A、B间的距离：先在AB外选一他点C，然后测出AC，BC的中点M、N，并测量出MN的长为18m，由此他就知道了A、B间的距离．下列有关他这次探究活动的结论中，错误的是( )
A．AB＝36mB．MN∥ABC．MN＝CBD．CM＝AC
3、（4分）要比较两名同学共六次数学测试中谁的成绩比较稳定，应选用的统计量为（ ）
A．中位数 B．方差 C．平均数 D．众数
4、（4分）如图，在△OAB中，∠AOB=55°，将△OAB在平面内绕点O顺时针旋转到△OA′B′ 的位置，使得BB′∥AO，则旋转角的度数为（ ）
A．125°B．70°C．55°D．15°
5、（4分）如图，直线y=kx+b与坐标轴的两交点分别为A（2，0）和B（0，-3），则不等式kx+b+3≤0的解为（ ）
A．x≤0 B．x≥0 C．x≥2 D．x≤2
6、（4分）学校测量了全校800名男生的身高，并进行了分组，已知身高在1.70~1.75（单位：m）这一组的频率为0.25，则该组共有男生（ ）
A．100名B．200名C．250名D．400名
7、（4分） “的3倍与3的差不大于8”，列出不等式是（ ）
A．B．
C．D．
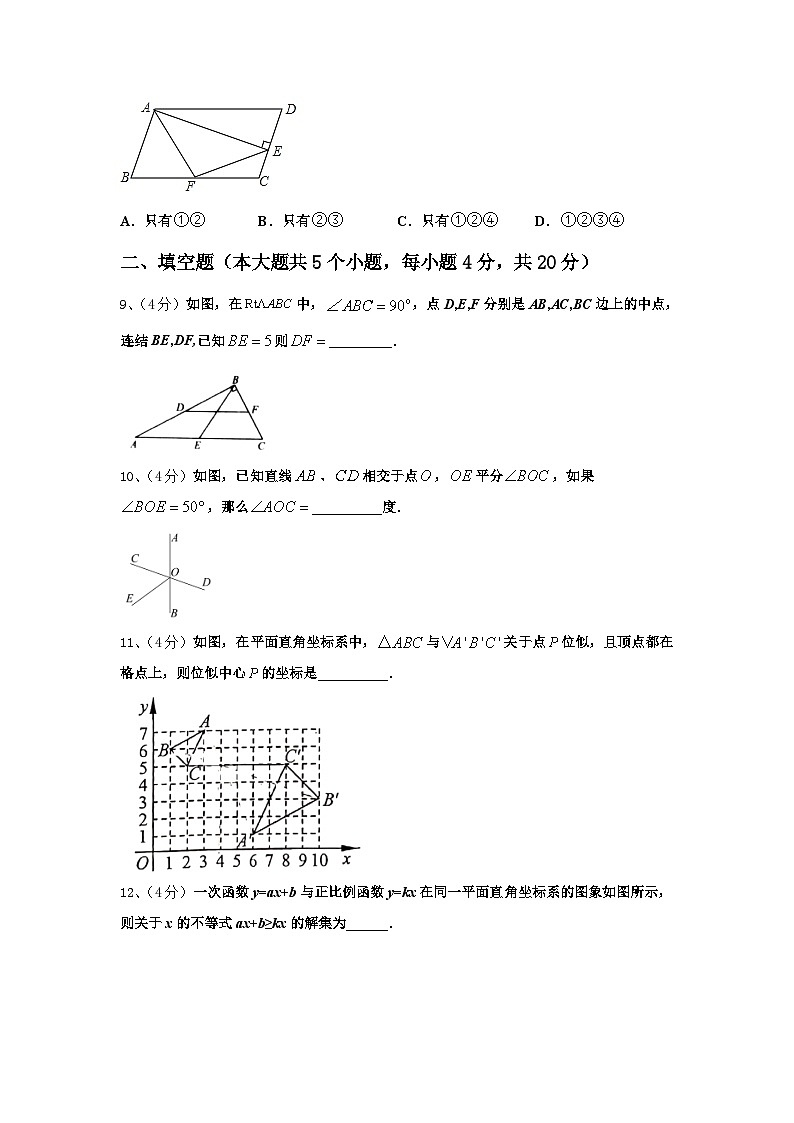
8、（4分）如图，▱ABCD中，，F是BC的中点，作，垂足E在线段CD上，连接EF、AF，下列结论：；；；中，一定成立的是
A．只有B．只有C．只有D．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图，在中，，点D,E,F分别是AB,AC,BC边上的中点，连结BE,DF,已知则_________．
10、（4分）如图，已知直线、相交于点，平分，如果，那么__________度．
11、（4分）如图，在平面直角坐标系中，与关于点位似，且顶点都在格点上，则位似中心的坐标是__________．
12、（4分）一次函数y=ax+b与正比例函数y=kx在同一平面直角坐标系的图象如图所示，则关于x的不等式ax+b≥kx的解集为______．
13、（4分）计算： _____________.
三、解答题（本大题共5个小题，共48分）
14、（12分）关于x、y的方程组的解满足x﹣2y≥1，求满足条件的k的最大整数值．
15、（8分）在▱ABCD中，点E、F分别在AB、CD上，且AE=CF．
（1）求证：△ADE≌△CBF；
（2）若DF=BF，求证：四边形DEBF为菱形．
16、（8分）一手机经销商计划购进某品牌的A型、B型、C型三款手机共60部，每款手机至少要购进8部，且恰好用完购机款61000元．设购进A型
手机x部，B型手机y部．三款手机的进价和预售价如下表：
（1）用含x，y的式子表示购进C型手机的部数；
（2）求出y与x之间的函数关系式；
（3）假设所购进手机全部售出，综合考虑各种因素，该手机经销商在购销这批手机过程中需另外支出各种费用共1500元．
①求出预估利润P（元）与x（部）的函数关系式；
（注：预估利润P＝预售总额-购机款-各种费用）
②求出预估利润的最大值，并写出此时购进三款手机各多少部．
17、（10分）甲，乙两人沿汀江绿道同地点，同方向运动，甲跑步，乙骑车，两人都匀速前行，若甲先出发60s，乙骑车追赶且速度是甲的两倍在运动的过程中，设甲，乙两人相距，乙骑车的时间为，y是t的函数，其图象的一部分如图所示，其中．
（1）甲的速度是多少；
（2）求a的值，并说明A点坐标的实际意义；
（3）当时，求y与t的函数关系式．
18、（10分）（1）提出问题：如图1，在正方形中，点E，H分别在BC，AB上，若于点O，求证；；
（2）类比探究：如图2，在正方形中，点B，E，G，F分别在AB，BC，CD，DA上，若于点O，探究线段EF与HG的数量关系，并说明理由；
（3）综合运用：在（2）问条件下，，如图3所示，已知，，求图中阴影部分的面积。
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）如图，在平行四边形ABCD中，连结AC，∠ABC=∠CAD=45°，AB=2，则BC=________ 。
20、（4分）如图，正方形ABCD中，AB=6，E是BC的中点，点P是对角线AC上一动点，则PE+PB的最小值为_____。
21、（4分）某商品的标价比成本高，当该商品降价出售时，为了不亏本，降价幅度不得超过，若用表示，则___．
22、（4分）化简:=_________.
23、（4分）最简二次根式与是同类二次根式，则＝________．
二、解答题（本大题共3个小题，共30分）
24、（8分）春节前小王花1200元从农贸市场购进批发价分别为每箱30元与50元的A,B两种水果进行销售，并分别以每箱35元与60元的价格出售，设购进A水果x箱，B水果y箱.
(1)让小王将水果全部售出共赚了215元，则小王共购进A、B水果各多少箱?
(2)若要求购进A水果的数量不得少于B水果的数量，则应该如何分配购进A, B水果的数量并全部售出才能获得最大利润，此时最大利润是多少?
25、（10分）运城市某学校去年在某商场购买甲、乙两种不同足球，购买甲种足球共花费2000元，购买乙种足球共花费1400元，购买甲种足球数量是购买乙种足球数量的2倍.且购买一个乙种足球比购买一个甲种足球多花20元.
（1）求购买一个甲种足球、一个乙种足球各需多少元；
（2）今年为响应“足球进校园”的号召，这所学校决定再次购买甲、乙两种足球共50个.恰逢该商场对两种足球的售价进行调整，甲种足球售价比第一次购买时提高了，乙种足球售价比第一次购买时降低了.如果此次购买甲、乙两种足球的总费用不超过3000元，那么这所学校最多可购买多少个乙种足球？
26、（12分）如图，矩形ABCD的对角线AC、BD相交于点O，点E、F在BD上，OE＝OF．
（1）求证：AE＝CF．
（2）若AB＝2，∠AOD＝120°，求矩形ABCD的面积．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、A
【解析】
由线段DE所代表的意思，结合装货半小时，可得出a的值，从而判断出①成立；结合路程=速度×时间，能得出甲车的速度，从而判断出②成立；设出乙车刚出发时的速度为x千米/时，则装满货后的速度为（x-50）千米/时，由路程=速度×时间列出关于x的一元一次方程，解出方程即可得知乙车的初始速度，由甲车先跑的路程÷两车速度差即可得出乙车追上甲车的时间，从而得出③成立；由乙车刚到达货站的时间，可以得出甲车行驶的总路程，结合A、B两地的距离即可判断④也成立．综上可知①②③④皆成立．
【详解】
∵线段DE代表乙车在途中的货站装货耗时半小时，
∴a=4+0.5=4.5(小时)，即①成立；
40分钟=小时，
甲车的速度为460÷(7+)=60(千米/时)，
即②成立；
设乙车刚出发时的速度为x千米/时,则装满货后的速度为(x−50)千米/时，
根据题意可知：4x+(7−4.5)( x−50)=460，
解得：x=90.
乙车发车时,甲车行驶的路程为60×23=40(千米)，
乙车追上甲车的时间为40÷(90−60)=(小时), 小时=80分钟，即③成立；
乙车刚到达货站时,甲车行驶的时间为(4+)小时，
此时甲车离B地的距离为460−60×(4+)=180(千米)，
即④成立.
综上可知正确的有：①②③④.
故选：A.
本题考查一次函数的应用——行程问题，解决此类题的关键是，要读懂图象，看清横纵坐标所代表的数学量，及每段图象所代表的情况.
2、C
【解析】
通过构造相似三角形即可解答.
【详解】
解：根据题意可得在△ABC中△ABC∽△MNC，
又因为M.N是AC，BC的中点，
所以相似比为2:1，MN//AB,B正确, CM=AC,D正确.
即AB=2MN=36，A正确;
MN=AB，C错误.
故本题选C.
本题考查相似三角形的判定与运用，熟悉掌握是解题关键.
3、B
【解析】分析：方差是用来衡量一组数据波动大小的量，中位数、众数、平均数是反映一组数据的集中程度
详解：由于方差反映数据的波动情况,所以要比较两名同学在四次数学测试中谁的成绩比较稳定，应选用的统计量是方差.
故选B.
点睛：本题考查了统计量的选取问题，熟练掌握各统计量的特征是解答本题的关键.中位数反映一组数据的中等水平，众数反映一组数据的多数水平，平均数反映一组数据的平均水平，方差反映一组数据的稳定程度，方差越大越不稳定，方差越小越稳定.
4、B
【解析】
据两直线平行，内错角相等可得，根据旋转的性质可得，然后利用等腰三角形两底角相等可得，即可得到旋转角的度数．
【详解】
，
，
又，
中，，
旋转角的度数为．
故选：．
本题考查了旋转的性质，等腰三角形两底角相等的性质，熟记性质并准确识图是解题的关键．
5、A．
【解析】
试题分析：由kx+b+3≤1得kx+b≤-3，
直线y=kx+b与y轴的交点为B（1，-3），
即当x=1时，y=-3，
∵函数值y随x的增大而增大，
∴当x≥1时，函数值kx+b≥-3，
∴不等式kx+b+3≥1的解集是x≥1．
故选A．
考点：一次函数与一元一次不等式．
6、B
【解析】
根据频数=总数×频率，直接代值计算即可．
【详解】
解：根据题意，得
该组共有男生为：800×0.25=200（人）．
故选：B．
此题考查频率、频数的关系：频率=。能够灵活运用公式是解题的关键．
7、A
【解析】
直接利用已知得出3x-3小于等于1即可．
【详解】
根据题意可得：3x-3≤1．
故选A．
此题主要考查了由实际问题抽象出一元一次不等式，正确理解题意是解题关键．
8、C
【解析】
利用平行四边形的性质：平行四边形的对边相等且平行，再由全等三角形的判定得出≌，利用全等三角形的性质得出对应线段之间关系进而得出答案．
【详解】
是BC的中点，
，
在▱ABCD中，，
，
，
，
，
，
，
，
，
故正确；
延长EF，交AB延长线于M，
四边形ABCD是平行四边形，
，
，
为BC中点，
，
在和中，
，
≌，
，，
，
，
，
，
，故正确；
，
，
，故错误；
设，则，
，
，
，
，
，故正确，
故选：C．
此题主要考查了平行四边形的性质以及全等三角形的判定与性质等知识，解决本题的关键是得出≌．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、1
【解析】
已知BE是Rt△ABC斜边AC的中线，那么BE=AC；EF是△ABC的中位线，则DF=AC，则DF=BE=1．
【详解】
解：，E为AC的中点，
，
分别为AB,BC的中点，
．
故答案为：1.
此题主要考查了三角形中位线定理以及直角三角形斜边上的中线等知识，用到的知识点为：（1）直角三角形斜边的中线等于斜边的一半；（2）三角形的中位线等于对应边的一半．
10、1
【解析】
先根据角平分线的定义，求出∠BOC的度数，再根据邻补角的和等于11°求解即可．
【详解】
解：∵平分，，
∴，
∴,
故答案为：1．
本题考查了角平分线的定义以及邻补角的性质，属于基础题．
11、
【解析】
根据位似中心的概念，直接连接对应的三点得到三条线，三条线的交点即为位似中心，读出坐标即可
【详解】
如图，连接AA’,BB’,CC’,三线的交点即为P点
读出P的坐标为
本题考查位似中心，能够找到位似中心是本题解题关键
12、x≥﹣1
【解析】
由图象可以知道，当x=-1时，两个函数的函数值是相等的，再根据函数的增减性可以判断出不等式ax+b≥kx解集．
【详解】
两个条直线的交点坐标为(−1, 2),且当x≥−1时,直线y=kx在y=ax+b直线的下方，故不等式ax+b≥kx的解集为x≥−1.
故答案为x≥−1.
本题考查了一次函数与一元一次不等式的知识点，解题的关键是根据图象可知一次函数与一元一次不等式的增减性.
13、1
【解析】
根据开平方运算的法则计算即可．
【详解】
1．
故答案为：1．
本题考查了实数的运算－开方运算，比较简单，注意符号的变化．
三、解答题（本大题共5个小题，共48分）
14、满足条件的k的最大整数值为1．
【解析】
将两方程相减得出x,y的值，再把x,y的值代入x﹣1y≥1，即可解答
【详解】
解关于x，y的方程组 ，得 ，
把它代入x﹣1y≥1得，3﹣k﹣1（3k﹣6）≥1，
解得k≤1，
所以满足条件的k的最大整数值为1．
此题考查二元一次方程组的解和解一元一次不等式，解题关键在于求出x,y的值再代入
15、（1）见解析；（2）见解析
【解析】
试题分析：（1）首先根据平行四边形的性质可得AD=BC，∠A=∠C，再加上条件AE=CF可利用SAS证明△ADE≌△CBF；
（2）首先证明DF=BE，再加上条件AB∥CD可得四边形DEBF是平行四边形，又DF=FB，可根据邻边相等的平行四边形为菱形证出结论．
试题解析：（1）∵四边形ABCD是平行四边形，
∴AD=BC，∠A=∠C，
∵在△ADE和△CBF中，
，
∴△ADE≌△CBF（SAS）；
（2）∵四边形ABCD是平行四边形，
∴AB∥CD，AB=CD，
∵AE=CF，
∴DF=EB，
∴四边形DEBF是平行四边形，
又∵DF=FB，
∴四边形DEBF为菱形．
考点：全等三角形的判定；菱形的判定；平行四边形的性质．
16、（1）60-x-y （2）y=2x-1 （3）①P=10x+10 ②最大值为1710元．
此时购进A型手机3部，B型手机18部，C型手机8部
【解析】
（1）手机经销商计划购进某品牌的A型、B型、C型三款手机共60部，设购进A型手机x部，B型手机y部，那么购进C型手机的部数=60-x-y；
（2）由题意，得 900x+1200y+1100（60-x-y）= 61000，
整理得 y=2x-1．
（3）①由题意，得 P= 1200x+1600y+1300（60-x-y）- 61000-110，
整理得 P=10x+10．
②购进C型手机部数为：60-x-y =110-3x．根据题意列不等式组，得
解得 29≤x≤3．
∴ x范围为29≤x≤3，且x为整数．
∵P是x的一次函数，k=10＞0，∴P随x的增大而增大．
∴当x取最大值3时，P有最大值，最大值为1710元．
此时购进A型手机3部，B型手机18部，C型手机8部．
点评：本题考查函数及其最值、不等式；解答本题的关键是掌握函数的概念和性质，会写函数的关系式，会求函数的最值，要求考生会求解不等式组的
17、（1）甲的速度为；（2），A点坐标的实际意义是：当乙骑车的时间是60 s时，乙追上甲；（3）当时，
【解析】
1根据图象中的数据和题意可以求得甲的速度；
2根据甲的速度可以求得乙的速度，再根据图象和题意即可求得点A的坐标和写出点A表示的实际意义；
3根据题意可以求得当t大于a时对应的函数解析式.
【详解】
（1）由题意可得，
甲的速度为：，
故答案为4；
（2）由1知，乙的速度为8 ，
依题意，可得
解得，，
点A的坐标为：，
A点坐标的实际意义是：当乙骑车的时间是60 s时，乙追上甲；
（3）由题意知，
当时，甲乙两人之间的距离是
即直线上另一点的坐标为，
当时，设y与t的函数关系式为：，
直线过点，，
，
解得：，
当时，
考查一次函数的应用，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．
18、（1）见解析；（2）EF=HG，理由见解析；（3）.
【解析】
（1）根据正方形的性质和已知条件可得：AB= DA，∠ABE=∠DAH=∠AOD =90°，根据同角的余角相等得出∠BAE=∠ADH，然后利用ASA即可证出△ABE≌△DAH，从而得出；
（2）过点D作DN∥GH交AB于N，过点A作AM∥FE交BC于M，根据（1）中结论，即可得出AM=DN，然后根据平行四边形的判定证出：四边形AMEF和四边形DNHG都是平行四边形，根据平行四边形的性质证出EF=AM，HG=DN，从而证出EF=HG；
（3）过点F作FP⊥BC于P，根据平行可证：△OFH∽OEG，∠FHO=∠EGO，列出比例式可得：，然后根据相似三角形的判定，证出△AHF∽△CGE，列出比例式，即可求出AF，然后根据矩形的判定可得四边形ABPF为矩形，再根据矩形的性质可得：BP=AF=1，PF=AB=4，利用勾股定理即可求出FE，从而算出FO、OE、HO和OG，最后根据三角形的面积公式计算面积即可.
【详解】
解：（1）∵四边形ABCD是正方形，
∴AB= DA，∠ABE=∠DAH=∠AOD =90°
∴∠BAE＋∠EAD=90°∠EAD＋∠ADH=90°
∴∠BAE=∠ADH
在△ABE和△DAH中
∴△ABE≌△DAH
∴；
（2）EF=HG，理由如下
过点D作DN∥GH交AB于N，过点A作AM∥FE交BC于M
∵，
∴AM⊥DN，
由（1）中结论可得：AM=DN
∵四边形ABCD是正方形，
∴AD∥BC，AB∥DC
∴四边形AMEF和四边形DNHG都是平行四边形
∴EF=AM，HG=DN
∴EF=HG；
（3）过点F作FP⊥BC于P
∵四边形ABCD是正方形，
∴AB=BC=，∠A=∠B=∠C=90°，AB∥CD
∴∠AHG=∠CGH
∵
∴△OFH∽OEG，∠FHO=∠EGO
∴，∠AHG－∠FHO=∠CGH－∠EGO
∴FO=，HO=，∠AHF=∠CGE
∴△AHF∽△CGE
∴
∴AF=
∵∠A=∠B=∠FPB=90°
∴四边形ABPF为矩形
∴BP=AF=1，PF=AB=4
∴PE=BE－BP=1
根据勾股定理可得：FE=
∴GH=FE=
∴FO=，EO=FE－FO=，HO==，OG=GH－HO=
∴S阴影=.
此题考查的是正方形的性质、全等三角形的判定及性质、平行四边形的判定及性质、相似三角形的判定及性质和勾股定理，掌握正方形的性质定理、全等三角形的判定定理及性质定理、平行四边形的判定定理及性质定理、相似三角形的判定定理及性质定理和用勾股定理解直角三角形是解决此题的关键.
一、填空题（本大题共5个小题，每小题4分，共20分）
19、
【解析】
证出△ACD是等腰直角三角形，由勾股定理求出AD，即可得出BC的长．
【详解】
四边形ABCD为平行四边形，CD=AB=2,BC=AD,∠D=∠ABC=∠CAD=45°
AC=CD=2,∠ACD=90°
△ACD为等腰直角三角形
∴BC=AD==.
故答案是：.
考查了平行四边形的性质、勾股定理、等腰直角三角形的判定与性质；熟练掌握平行四边形的性质，证明△ACD是等腰直角三角形是解决问题的关键．
20、3
【解析】
连接DE，交AC于点P，连接BD．点B与点D关于AC对称，DE的长即为PE+PB的最小值,根据勾股定理即可得出DE的长度.
【详解】
连接DE，交AC于点P，连接BD．
∵点B与点D关于AC对称，
∴DE的长即为PE+PB的最小值，
∵AB=6，E是BC的中点，
∴CE=3，
在Rt△CDE中，
DE=
=
=
=3.
故答案为3．
主要考查轴对称，勾股定理等考点的理解，作出辅助线得出DE的长即为PE+PB的最小值为解决本题的关键.
21、
【解析】
本题主要考查列代数式. 此题中最大的降价率即是保证售价和成本价相等，可以把成本价看作单位1，根据题意即可列式．
解：设成本价是1，则
（1+p%）（1-d%）=1．
1-d%=，
22、
【解析】
根据三角形法则计算即可解决问题．
【详解】
解：原式=，
= ，
= ，
=.
故答案为.
本题考查平面向量、三角形法则等知识，解题的关键是灵活运用三角形法则解决问题，属于中考基础题．
23、21
【解析】
根据二次根式及同类二次根式的定义列出方程组即可求出答案.
【详解】
∵最简二次根式与是同类二次根式，
∴ ，
解得，，
∴
故答案为21.
二、解答题（本大题共3个小题，共30分）
24、（1）小王共购进A水果25箱，B水果9箱；（2）应购进A水果15箱、B水果15箱能够获得最大利润，最大利润为225元.
【解析】
（1）根据题意中的相等关系“A种水果x箱的批发价+B种水果y箱的批发价=1200元，A种水果赚的钱+B种水果赚的钱=215元”列方程组求解即可；
（2）先用x表示y，列出利润w的关系式，再根据题意求出x的取值范围，然后根据一次函数的性质求出w的最大值及购进方案.
【详解】
解：（1）根据题意，得
，即，解得.
答：小王共购进A水果25箱，B水果9箱.
（2）设获得的利润为w元，根据题意得，
∵，∴，
∵A水果的数量不得少于B水果的数量，
∴，即，解得.
∴，
∵，∴w随x的增大而减小，
∴当x=15时，w最大=225，此时.
即应购进A水果15箱、B水果15箱能够获得最大利润，最大利润为225元.
本题考查了二元一次方程组的应用、一元一次不等式的解法和一次函数的性质，正确理解题意列出方程组、灵活应用一次函数的性质是解此题的关键.
25、（1）购买一个甲种足球需50元，购买一个乙种足球需70元；（2）最多可购买31个乙种足球.
【解析】
（1）设购买一个甲种足球需x元，根据：购买足球数＝总费用÷单价，购买甲种足球的数量＝2×购买乙种足球数量，列出方程求解即可；
（2）设这所学校再次购买y个乙种足球，根据：购买甲足球费用＋购买乙足球费用≤3000，列出不等式，求解得结论．
【详解】
（1）解：设购买一个甲种足球需元，则购买一个乙种足球需元，
由题意得：，
解得：
经检验，是原方程的解，
答：购买一个甲种足球需50元，购买一个乙种足球需70元.
（2）设这所学校再次购买个乙种足球，则购买个甲种足球，
由题意得：
解得：，
答：最多可购买31个乙种足球.
本题解题关键：在于弄清已知数与所求量的数量关系，建立联系，特别注意的是分式方程在应用题里面也需要检验.
26、（1）见解析；（2）4
【解析】
（1）由矩形的性质得出OA=OC，OB=OD，AC=BD，∠ABC=90°，证出OE=OF，由SAS证明△AOE≌△COF，即可得出AE=CF；
（2）证出△AOB是等边三角形，得出OA=AB=2，AC=2OA=4，在Rt△ABC中，由勾股定理求出BC= =，即可得出矩形ABCD的面积．
【详解】
(1）证明：∵四边形ABCD是矩形，
∴OA＝OC，
在△AOE和△COF中，
，
∴△AOE≌△COF（SAS），
∴AE＝CF；
（2）解：∠AOD＝120°，
所以，∠AOB＝60°，
∵OA＝OC，OB＝OD，AC＝BD，
∴OA＝OB，
∴△AOB是等边三角形，
∴OA＝AB＝2，
∴AC＝2OA＝4，
在Rt△ABC中，BC＝，
∴矩形ABCD的面积＝AB•BC＝2×2＝4．
此题考查全等三角形的判定与性质，矩形的性质，解题关键在于利用勾股定理进行计算
题号
一
二
三
四
五
总分
得分
批阅人
手机型号
A型
B型
C型
进 价（单位：元/部）
900
1200
1100
预售价（单位：元/部）
1200
1600
1300