






所属成套资源:沪教版(2020)数学必修第二册PPT课件+分层练习整册(含单元复习课件+单元测试卷)
沪教版(2020)必修第二册2余弦定理完美版教学课件ppt
展开
这是一份沪教版(2020)必修第二册2余弦定理完美版教学课件ppt,共22页。PPT课件主要包含了学习目标,知识回顾,新课讲解,课本练习,随堂检测,余弦定理,课堂小结等内容,欢迎下载使用。
1.掌握余弦定理的证明方法,牢记余弦定理公式.2.能够从余弦定理得到它的推论.3.能够应用余弦定理及其推论解三角形.
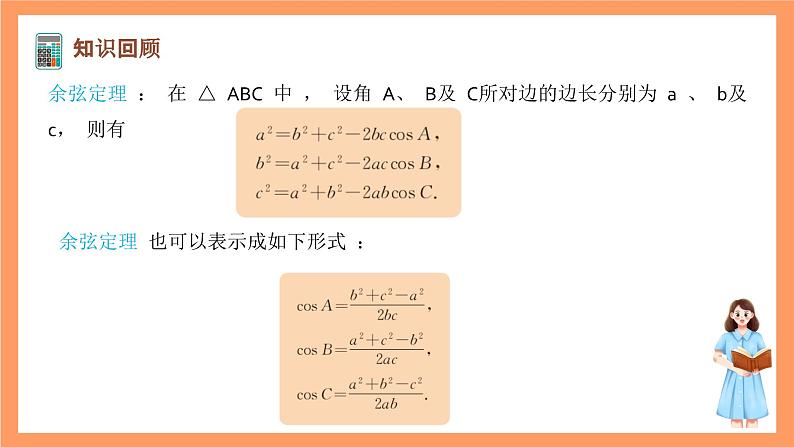
余弦定理 : 在 △ ABC 中 , 设角 A、 B及 C所对边的边长分别为 a 、 b及 c, 则有
余弦定理 也可以表示成如下形式 :
求证 : △ ABC 为等边三角形
即 cos B=cosC
又由 B 、 C ∈ ( 0 , π ), 得 B= C , 从而 b =c . 再由
所以 , △ ABC为等边三角形 .
例 8 在 △ ABC 中 , 已知 a=5 , b =4 , 且三角形面积S=8. 求 c .
为了表示例 8 中的角 C, 我们引入如下记号
一般地 , 我们用 arcsin a表示满足 sin x = a( 0≤ a ≤1 ) 的角
例 9 根据下列条件 , 分别求角 x :
( 3 ) 设锐角 α 满足 tan α =3 , 就有 α =arctan3. 因为 tan ( - α )=-tan α =-3 , 所以原式等价于求解 tan x =tan ( - α ), 从而有x = k π+ ( -arctan3 ), k∈Z.
所以 x=π-arctan3.
2. 证明 : 平行四边形中 , 四边平方和等于对角线平方和 .
证明:设平行四边形为 ABCD,以A为原点,AB所在直线为x轴,建立直角坐标系.设B(a,0),D(m,n),则C(m+a,n).于是
3. 在 △ ABC 中 , 求证 :
4. 分别求满足下列条件的角 .
2. 余弦定理的推论:
3. 用余弦定理可以解决两种解三角形的题型:(1) 已知三边解三角形.(2) 已知两边及一角解三角形.
相关课件
这是一份高中沪教版(2020)1向量的投影一等奖教学ppt课件,共29页。PPT课件主要包含了学习目标,1向量的投影,课本练习,随堂检测等内容,欢迎下载使用。
这是一份数学必修第二册3实数与向量的乘法精品教学课件ppt,共1页。
这是一份高中数学沪教版(2020)必修第二册2正弦函数的性质评优课教学ppt课件,共1页。











