初中数学浙教版（2024）九年级上册第4章 相似三角形4.4 两个三角形相似的判定课文课件ppt

这是一份初中数学浙教版（2024）九年级上册第4章 相似三角形4.4 两个三角形相似的判定课文课件ppt，共19页。PPT课件主要包含了学习目标，问题导入，新知探究，两角对应相等，三边对应成比例，∵DE∥BC，下面给出证明，典例精讲，课堂小结，当堂检测等内容，欢迎下载使用。

掌握判定三角形相似的预备定理，并了解它的证明过程.掌握利用两角判定三角形相似的定理，了解证明过程，并会根据相似三角形的判定定理判定两个三角形相似.能利用三角形的相似解决简单的实际问题.
怎样运用三角形的相似测量河的宽度？
在解决这个问题之前，我们先思考：判定两个三角形相似需要多少条件？
回顾判定两个三角形全等的条件，相应的，猜想判定两个三角形相似有哪些条件？
两个三角形全等的条件：
AAS，ASA，SAS，SSS，HL.
两边对应成比例，且夹角相等
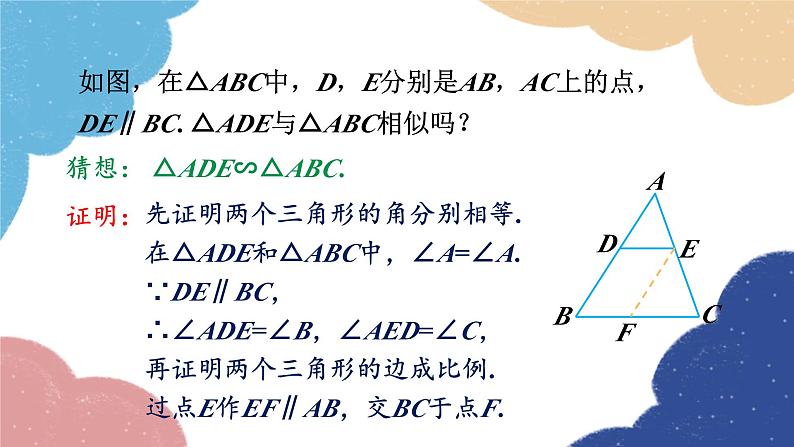
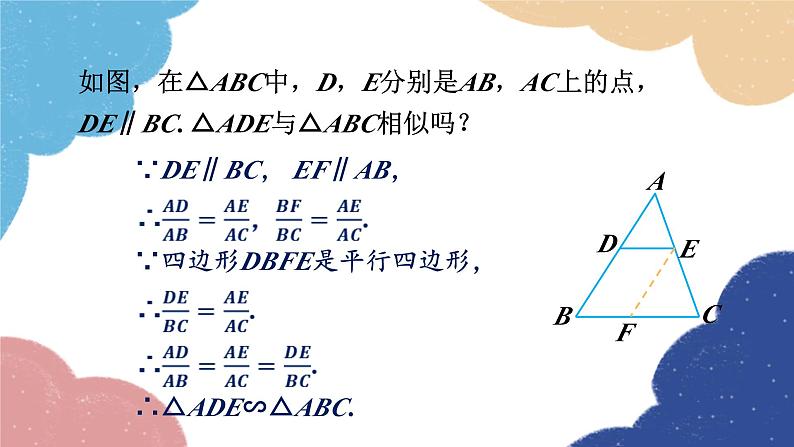
如图，在△ABC中，D，E分别是AB，AC上的点，DE∥BC. △ADE与△ABC相似吗？
猜想： △ADE∽△ABC.
先证明两个三角形的角分别相等.
在△ADE和△ABC中，∠A=∠A.
∴∠ADE=∠B，∠AED=∠C，
再证明两个三角形的边成比例.
过点E作EF∥AB，交BC于点F.
∵DE∥BC， EF∥AB，
∵四边形DBFE是平行四边形，
∴△ADE∽△ABC.
判定三角形相似的预备定理：平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似.
根据上述预备定理，我们可以得到以下三角形相似的判定定理：有两个角对应相等的两个三角形相似.
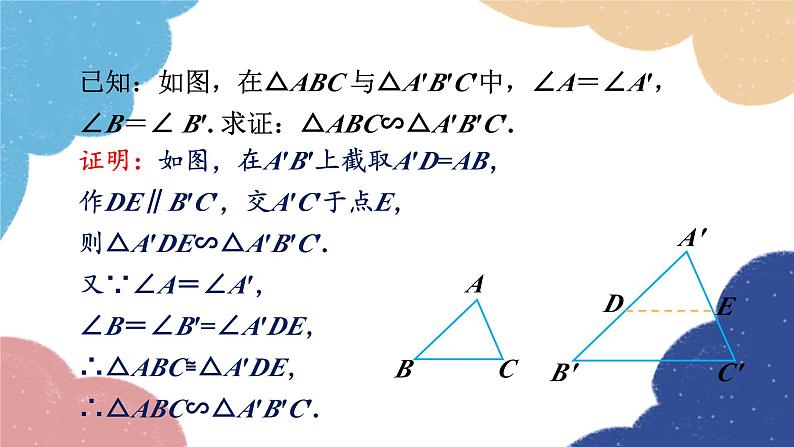
证明：如图，在A′B′上截取A′D=AB，作DE∥B′C′，交A′C′于点E，则△A′DE∽△A′B′C′.又∵∠A＝∠A′，∠B＝∠B′=∠A′DE，∴△ABC≌△A′DE，∴△ABC∽△A′B′C′.
已知：如图，在△ABC 与△A′B′C′中，∠A＝∠A′，∠B＝∠ B′. 求证：△ABC∽△A′B′C′.
由两角对应相等判定三角形相似是所有判定方法中最常用的方法之一，其关键是找准对应角，解题时应注意挖掘公共角、对顶角、同角的余角（或补角）等相等关系.常见的基本图形如下：
（1）若∠ADE=∠B，则有△ADE∽△ABC；
（2）若∠CDE=∠A，则有△ABC∽△DEC；
（3）若∠CDA=∠CAB，则有△ABC∽△DAC；
（4）若∠A=∠C，则有△OAB∽△OCD；
（5）若∠B=∠E，则有△AED∽△ABC.
例1 在一次数学活动课上，为了测量河宽AB，小聪采用如下方法：从A处沿与AB垂直的直线方向走45 m到达C处，插一根标杆，然后沿同方向继续走15 m到达D处，再右转90°走到E处，使B，C，E三点恰好在一条直线上. 量得DE=20 m，这样就可以求出河宽AB. 请你说明理由，并算出结果.
类似地，顶角（或底角）相等的两个等腰三角形相似.任意两个等边三角形都相似.
一对锐角相等的两个直角三角形相似.
三角形相似的判定定理：有两个角对应相等的两个三角形相似.
1.能否判定如图△ABC与△A′B′C′相似？为什么？
解：能判定这两个三角形相似. 理由如下：∵∠C=180°-∠A-∠B=180°-105°-35°=40°，∴∠C=∠C′.又∵∠A=∠A′，∴△ABC∽△A′B′C′.
2.如图，点D，E，F分别在△ABC的各条边上，且DE∥BC，DF∥AC. 请尽可能多地找出图中的相似三角形，并说明理由.
解：（1）△ADE∽△ABC. 理由如下：∵DE∥BC，∴△ADE∽△ABC.（2）△DBF∽△ABC. 理由如下：∵DF∥AC，∴△DBF∽△ABC.
（3）△ADE∽△DBF. 理由如下：∵DE∥BC，∴∠ADE=∠DBF，∠EDF=∠DFB.又∵DF∥AC，∴∠EDF=∠AED.∴∠DFB=∠AED.∴△ADE∽△DBF.