




所属成套资源:沪教版(五四制)数学九年级上册PPT课件+题型专训(原卷+解析卷)整套(含单元综合检测重难点)
初中沪教版(五四制)(2024)24.4 相似三角形的判定优秀课后复习题
展开
这是一份初中沪教版(五四制)(2024)24.4 相似三角形的判定优秀课后复习题,文件包含沪教版五四制数学九上244《相似三角形的判定》判定定理1和2题型专训原卷版docx、沪教版五四制数学九上244《相似三角形的判定》判定定理1和2题型专训解析版docx等2份试卷配套教学资源,其中试卷共38页, 欢迎下载使用。
一、相似三角形
在和中,如果我们就说与相似,记作∽.k就是它们的相似比,“∽”读作“相似于”.
要点:
(1)书写两个三角形相似时,要注意对应点的位置要一致,即∽,则说明点A的对应点是A′,点B的对应点是B′,点C的对应点是C′;
(2)对于相似比,要注意顺序和对应的问题,如果两个三角形相似,那么第一个三角形的一边和第二个三角形的对应边的比叫做第一个三角形和第二个三角形的相似比.当相似比为1时,两个三角形全等.
二、相似三角形的判定定理
1.预备定理:平行于三角形一边的直线和其他两边相交,所构成的三角形和原三角形相似.
2.判定定理(一):如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
3.判定定理(二):如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.
要点:
此方法要求用三角形的两边及其夹角来判定两个三角形相似,应用时必须注意这个角必需是两边的夹角,否则,判断的结果可能是错误的.
过关检测
目录:一、判定定理1;二、判定定理2;三、判定定理1和2综合。
一、判定定理1
一、解答题
1.已知:如图所示,相交于点O,连接,且,求证:.
2.如图,在Rt△ABC中,∠B=90°,点D在AC边上,交BC于点E.求证:.
3.如图,在中,,于D.
求证:.
4.如图,DA⊥AB于A,EB⊥AB于B,C是AB上的动点,若∠DCE=90°.求证:△ACD∽△BEC
5.如图,Rt△ABC中,,于F,AD是∠BAC的平分线,交AC于G,AD与BF交于点E.
(1)求证:
(2) , .
6.已知:如图,在△ABC和△A′B′C′中,∠A=∠A′,∠B=∠B′.求证:△ABC∽△A′B′C′.
7.如图,在△ABC中,∠ABC=2∠C,点E为AC的中点,AD⊥BC于点D,ED延长后交AB的延长线于点F,求证:△AEF∽△ABC.
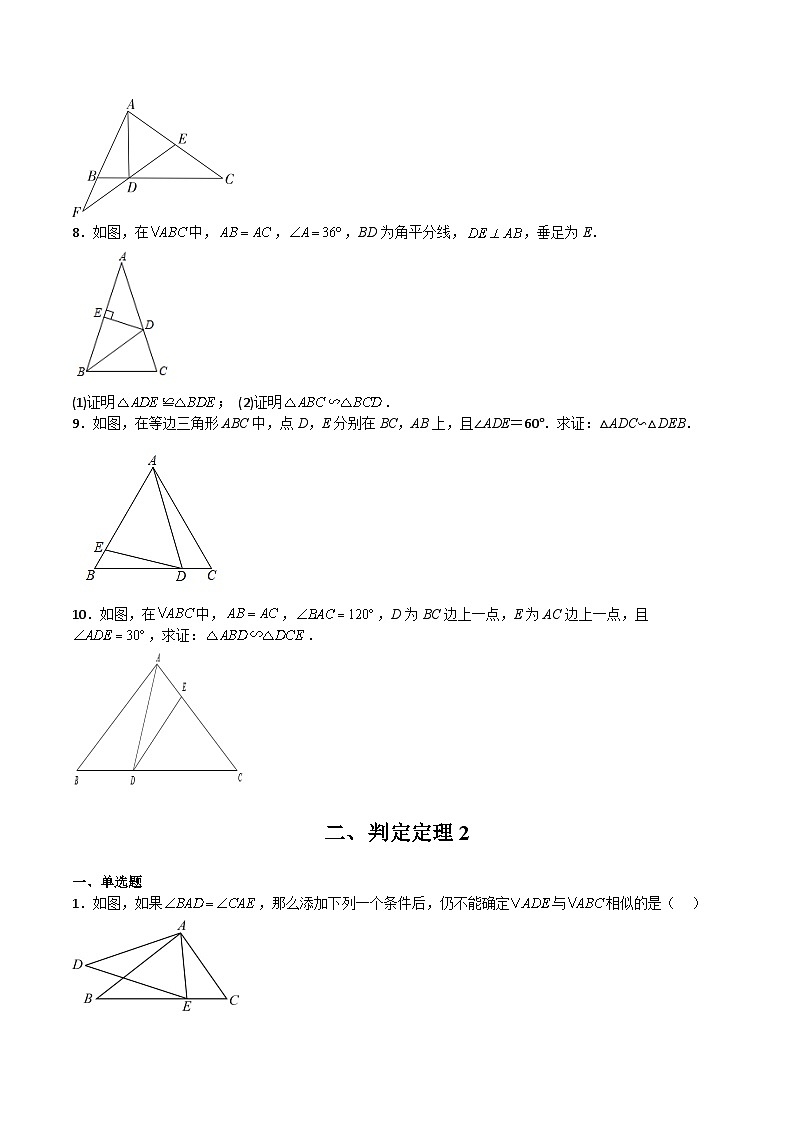
8.如图,在中,,,BD为角平分线,,垂足为E.
(1)证明; (2)证明.
9.如图,在等边三角形ABC中,点D,E分别在BC,AB上,且∠ADE=60°.求证:△ADC∽△DEB.
10.如图,在中,,,D为BC边上一点,E为AC边上一点,且,求证:.
二、判定定理2
一、单选题
1.如图,如果,那么添加下列一个条件后,仍不能确定与相似的是( )
A.B.C.D.
2.如图,下列条件能使△BPE和△CPD相似的有( )
①∠B=∠C;②;③∠ADB=∠AEC;④;⑤.
A.2个B.3个C.4个D.5个
二、解答题
3.已知:D、E是的边、上的点,,求证:.
4.如图,在中,,D是边上一点,.求证.
5.如图,与交于点,,,,,求证:.
6.如图,P是的边上的一点.
(1)如果,与是否相似?为什么?
(2)如果,与是否相似?为什么?如果呢?
7.如图,,,,点、、在同一条直线上.求证:.
8.如图,已知E是的中线AD上一点,且.求证:.
9.如图,已知∠BAE=∠CAD,AB=18,AC=48,AE=15,AD=40.
求证:△ABC∽△AED.
三、判定定理1和2综合
一、单选题
1.含角的直角三角板与含角的直角三角板如图放置,它们的斜边与斜边相交于点E.下列结论正确的是( )
A.B.
C.D.
2.如图,点在的边上,若要判定,则下列添加的条件不正确的是
A.B.C.D.
3.张老师在编写下面这个题目的答案时,不小心打乱了解答过程的顺序,你能帮他调整过来吗?证明步骤正确的顺序是( )
已知:如图,在中,点D,E,F分别在边,,上,且,.求证:.
证明:①又∵,②∵,③∴,④∴,⑤∴.
A.③②④①⑤B.②④①③⑤C.③①④②⑤D.②③④①⑤
二、填空题
4.中,为上一点,为上一点,添加一个条件________(只能填一个)可以使得与相似.
5.如图,已知:在和中,若,请添加一个条件______,使.(写一个即可)
6.如图,已知,请再添加一个条件,使,你添加的条件是________(写出一个即可).
7.已知:如图,点在边上,若______时,则.
8.如图D,E两点分别在线段和上,在下列四个条件中:①;②;③;④.其中能使与相似的是_______.(填序号)
三、解答题
9.如图,在中和中,,,,和相似吗?为什么?
10.如图,在平行四边形中,点为边上一点,连接,点为线段上一点,且,求证:.
11.如图,在△ABC中,点D是AB上一点,且AD=1,AB=3,.
求证:△ACD∽△ABC.
12.已知:中,,,用尺规求作一条过点B的直线,使得截出的一个三角形与相似并证明.(保留作图痕迹,不写作法)
13.如图,在中,CD是斜边AB上的高.
求证:.
14.如图,在中,平分,点E在上,且.
(1)求证:;
(2)若,,求的值.
15.如图,为的角平分线,的垂直平分线交的延长线于E,交于F,连接.求证:.
16.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,且AD=8,BD=2,Rt△FEG的直角顶点E在AC边上运动,一条直角边EG经过点B,且与CD交于点N,另一条直角边EF与AB交于点M.
(1)求证:△AEM∽△CBN;
(2)若E是AC的四等分点,求的值.
相关试卷
这是一份初中第一节 二次函数的概念精品同步达标检测题,文件包含沪教版五四制数学九上261《二次函数的概念》题型专训原卷版docx、沪教版五四制数学九上261《二次函数的概念》题型专训解析版docx等2份试卷配套教学资源,其中试卷共20页, 欢迎下载使用。
这是一份初中数学沪教版(五四制)(2024)九年级上册第二十五章 锐角的三角比第一节 锐角的三角比25.2 求锐角的三角比的值精品一课一练,文件包含沪教版五四制数学九上252《求锐角的三角比的值》题型专训原卷版docx、沪教版五四制数学九上252《求锐角的三角比的值》题型专训解析版docx等2份试卷配套教学资源,其中试卷共25页, 欢迎下载使用。
这是一份初中数学沪教版(五四制)(2024)九年级上册第二十四章 相似三角形第四节 平面向量的线性运算24.7 向量的线性运算精品习题,文件包含沪教版五四制数学九上246-247《平面向量的线性运算》题型专训原卷版docx、沪教版五四制数学九上246-247《平面向量的线性运算》题型专训解析版docx等2份试卷配套教学资源,其中试卷共45页, 欢迎下载使用。










