初中数学沪教版（五四制）（2024）九年级上册第二十五章 锐角的三角比第一节 锐角的三角比25.2 求锐角的三角比的值精品一课一练

这是一份初中数学沪教版（五四制）（2024）九年级上册第二十五章 锐角的三角比第一节 锐角的三角比25.2 求锐角的三角比的值精品一课一练，文件包含沪教版五四制数学九上252《求锐角的三角比的值》题型专训原卷版docx、沪教版五四制数学九上252《求锐角的三角比的值》题型专训解析版docx等2份试卷配套教学资源，其中试卷共25页， 欢迎下载使用。

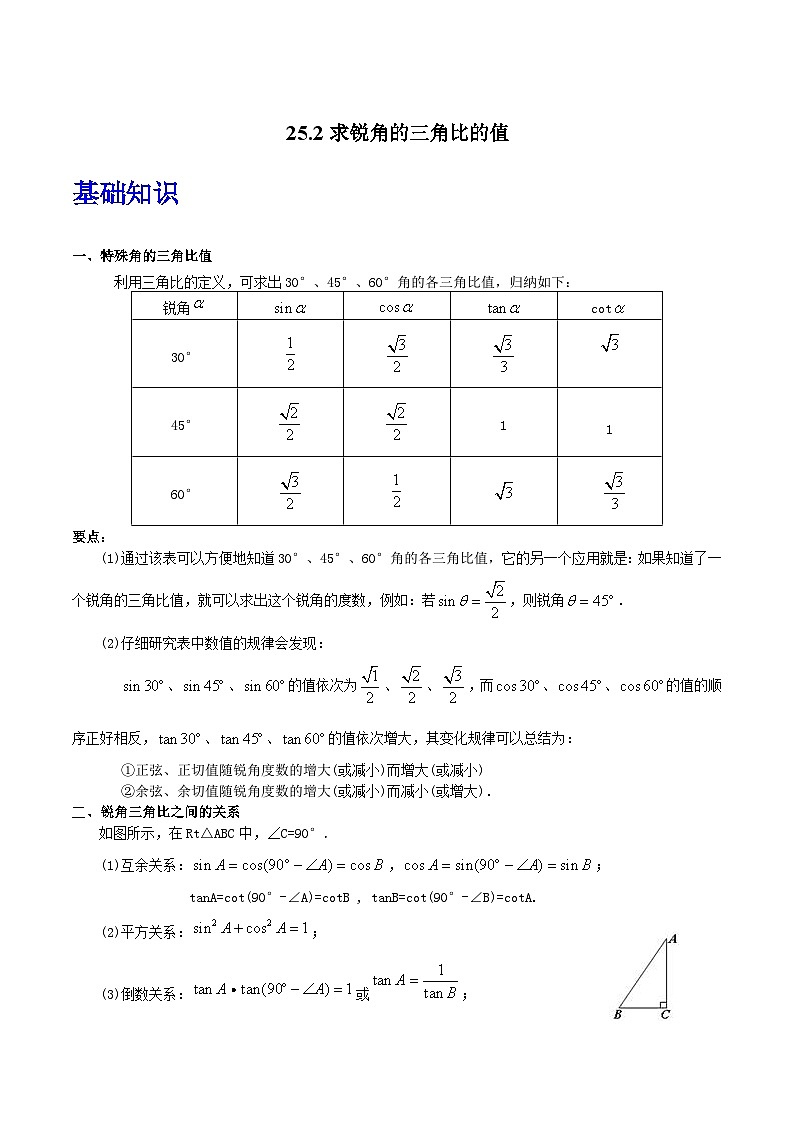
一、特殊角的三角比值
利用三角比的定义，可求出30°、45°、60°角的各三角比值，归纳如下：
要点：
(1)通过该表可以方便地知道30°、45°、60°角的各三角比值，它的另一个应用就是：如果知道了一个锐角的三角比值，就可以求出这个锐角的度数，例如：若，则锐角．
(2)仔细研究表中数值的规律会发现：
、、的值依次为、、，而、、的值的顺序正好相反，、、的值依次增大，其变化规律可以总结为：
①正弦、正切值随锐角度数的增大(或减小)而增大(或减小)
②余弦、余切值随锐角度数的增大(或减小)而减小(或增大)．
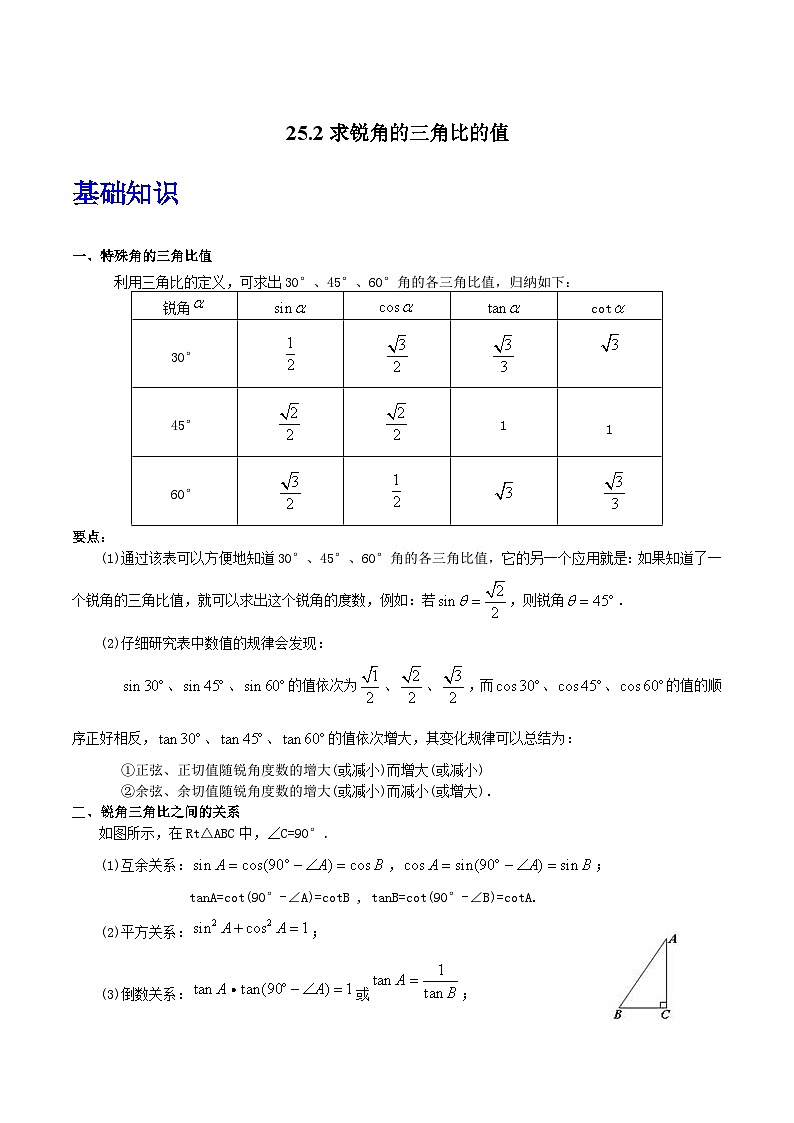
二、锐角三角比之间的关系
如图所示，在Rt△ABC中，∠C=90°．
(1)互余关系：，；
tanA=ct(90°-∠A)=ctB , tanB=ct(90°-∠B)=ctA.
(2)平方关系：；
(3)倒数关系：或；
(4)商的关系：
要点：
锐角三角比之间的关系式可由锐角三角比的意义推导得出，常应用在三角比的计算中，计算时巧用这些关系式可使运算简便．
过关检测
一、单选题
1．计算的结果为（ ）
A．B．1C．D．
【答案】C
【分析】根据特殊角的三角函数值进行计算即可．
【解析】解：
故选：C．
【点睛】本题考查特殊角的三角函数值，熟记各特殊角的三角函数值是解答此题的关键．
2．的值等于( )
A．B．C．D．1
【答案】A
【分析】根据进行计算即可得出答案．
【解析】解：．
故选A．
【点睛】本题考查了特殊角的三角函数值．牢记特殊角的三角函数值是解题的关键．
3．下列三角函数中，结果为的是（ ）
A．B．C．D．
【答案】D
【分析】根据特殊角的三角函数值解答即可得到答案．
【解析】解：A.，不符合题意，选项错误；
B.，不符合题意，选项错误；
C.，不符合题意，选项错误；
D.，符合题意，选项正确，
故选：D．
【点睛】本题考查了特殊角的三角函数值，熟记特殊角的三角函数值是解题关键．
4．如果锐角的正切值是，则下列结论正确的是（ ）
A．B．C．D．
【答案】A
【分析】利用30度角和45度角的正切值与角的正切值比较，即可得到答案．
【解析】解：∵，，，，，，
而，
∴，
∴，
∴，
故选：A．
【点睛】此题考查各角的正切值，实数的平方运算，实数的大小比较，熟记各特殊角的三角函数值是解题的关键．
5．按科学记算器，使显示器显示后，求的值，以下按键顺序正确的是( )
A． B．C． D．
【答案】C
【分析】根据计算器的使用进行按键即可求解．
【解析】解：显示器显示D后，即弧度制；
求的值，需按顺序按下：，，．
故选：C.
【点睛】本题考查了用过计算器计算三角函数，会用科学记算器进行计算是解题关键．
6．已知实数，则下列说法正确的是（ ）
A．B．C．D．
【答案】A
【分析】分别求出各三角函数的值，然后比较他们的大小即可.
【解析】解：，
∵，
∴，
故选：A.
【点睛】本题主要是考查特殊角的三角函数值，属于基础题，解答本题的关键是熟练掌握特殊角的所有三角函数值，所以要牢记特殊角的三角函数值，另外还考查了实数比较大小.
7．如果，那么与的差（ ）
A．大于0B．小于0C．等于0D．不能确定
【答案】B
【分析】，再根据正弦函数随着角的增大而增大进行分析即可．
【解析】∵，正弦函数随着角的增大而增大，
∴当时，，
，即，
故选B．
【点睛】本题考查了锐角三角函数的增减性，正弦函数值随着角的增大而增大．
8．化简等于（ ）
A．B．0
C．D．以上都不对
【答案】C
【分析】根据二次根式的性质得出，然后化为同名三角函数，根据三角函数的增减性化简即可求解．
【解析】解：，
∵，
∴原式，
故选：C．
【点睛】本题考查了三角函数关系，掌握三角函数的增减性是解题的关键．
9．定义一种运算：，例如：当，时，，则的值为( )
A．B．C．D．
【答案】B
【分析】根据，可以计算出的值．
【解析】解：由题意可得，





，
故选：B．
【点睛】本题考查解直角三角形、二次根式的混合运算、新定义，解答本题的关键是明确题意，利用新定义解答．
10．我国南宋著名数学家秦九韶在他的著作《数学九章》一书中，给出了这样的一个结论：三边分别为a、b、c的的面积为．的边a、b、c所对的角分别是∠A、∠B、∠C，则．下列结论中正确的是（ ）
A．B．
C．D．
【答案】A
【分析】本题利用三角函数间的关系和面积相等进行变形解题即可．
【解析】解：∵，，
∴
即，
，
，
故选：A．
【点睛】本题考查等式利用等式的性质解题化简，熟悉是解题的关键．
二、填空题
11．填空：
； ； ， ．
【答案】
【分析】根据特殊角的三角函数值直接求解．
【解析】解：；；；．
故答案为：；1；；．
【点睛】本题考查特殊角的三角函数值，属于基础题，熟记特殊角的三角函数值是解题的关键．
12．计算：
【答案】
【分析】根据特殊角三角函数代入求解即可得到答案；
【解析】解：原式，
故答案为：．
【点睛】本题考查特殊角三角函数混合运算，解题的关键是熟练掌握特殊角三角函数值
13．已知是锐角，且，那么 ．
【答案】/45度
【分析】直接根据特殊角的三角函数值解答即可．
【解析】∵，
∴．
故答案为：．
【点睛】本题主要考查了特殊角的三角函数值，记忆特殊角的三角函数值是解题的关键．
14．在中，，若，则 ．
【答案】/0.75
【分析】根据一个角的余弦等于它余角的正弦，可得答案．
【解析】解：如图，，．
∵，
∴．
故答案为：．
【点睛】本题考查三角函数的定义．由定义推出互余两角的三角函数的关系：若，则是解题关键．
15．已知α为锐角，且，则 °．
【答案】20
【分析】根据求解即可．
【解析】解：∵α为锐角，且，
∴，则，
故答案为：20．
【点睛】本题考查特殊角的三角函数值，熟记特殊角的三角函数值是解答的关键．
16．如图，△ABC在边长为1个单位的方格纸中，△ABC的顶点在小正方形顶点位置，那么∠ABC的正切值为 ．
【答案】/0.5
【分析】根据题意和图形，可以求得、和的长，然后根据勾股定理的逆定理可以判断的形状，然后即可求得的正弦值．
【解析】解：由图可得，，，．
∴，
∴是直角三角形，
∴，
故答案为：．
【点睛】本题考查勾股定理的逆定理、解直角三角形，解答本题的关键是明确题意，利用数形结合的思想解答．
17．在中，，则的形状是 ．
【答案】等边三角形
【分析】先根据非负数的性质求出，，再根据三角函数作答．
【解析】∵，
∴，，
即，，
∴，，
∴，
则一定是等边三角形，
故答案为:等边三角形．
【点睛】本题考查了非负数的性质，三角函数，等边三角形的判定，数量掌握特殊角的三角函数值是解题的关键．
18．将一副三角尺（在Rt△ABC中，∠ACB＝90°，∠B＝60°；在Rt△EDF中，∠EDF＝90°，∠E＝45°）如图摆放，点D为AB的中点，DE交AC于点P，DF经过点C．将△EDF绕点D顺时针方向旋转角，交AC于点M，交BC于点N，则的值为 ．
【答案】
【分析】先根据直角三角形斜边上的中线性质得CD=AD=DB，则∠ACD=∠A=30°，∠BCD=∠B=60°，由于∠EDF=90°，可利用互余得∠CPD=60°，再根据旋转的性质得∠PDM=∠CDN=α，于是可判断△PDM∽△CDN，得到，然后在Rt△PCD中利用正切的定义得到，继而根据面积比等于相似比即可求解．
【解析】解：∵点D为斜边AB的中点，
∴CD=AD=DB，
∴∠ACD=∠A=30°，∠BCD=∠B=60°，
∵∠EDF=90°，
∴∠CPD=60°，
∴∠MPD=∠NCD，
∵△EDF绕点D顺时针方向旋转α（0°＜α＜60°），
∴∠PDM=∠CDN=α，
∴△PDM∽△CDN，
∴，
在Rt△PCD中，∵，
∴．
故答案为：
【点睛】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了相似三角形的判定与性质，以及特殊角的三角函数值．
三、解答题
19．计算：．
【答案】
【分析】根据完全平方公式可得，再开方得，即可运算出结果．
【解析】原式=，
，
．
【点睛】本题考查利用特殊角的锐角三角比的值进行实数计算，利用完全平方公式化简，并能熟记特殊值的三角函数值是解题的关键．
20．计算：．
【答案】
【分析】直接利用特殊角三角函数值，代入值就可以求得结果．
【解析】解：原式
．
【点睛】本题主要考查利用特殊角的锐角三角函数的混合运算，熟练掌握特殊角的三角函数值是解题关键．
21．计算： ．
【答案】
【分析】把特殊角的三角函数值代入计算即可．
【解析】解：原式
．
【点睛】本题考查的是特殊角的三角函数值，熟记特殊角的三角函数值是解题的关键．
22．计算： ．
【答案】
【分析】直接利用特殊角的三角函数值代入求出答案．
【解析】解：原式
【点睛】此题主要考查了特殊角的三角函数值，正确记忆相关数据是解题关键．
23．计算：．
【答案】
【分析】分别把各特殊角的三角函数值代入进行计算即可．
【解析】解：
【点睛】本题考查了三角函数值的混合运算，熟记各特殊角的三角函数值是解题的关键．
24．计算：．
【答案】
【分析】先将特殊角的三角函数值代入，再进行二次根式的计算即可．
【解析】
．
【点睛】本题考查了特殊角的三角函数值，以及二次根式的混合运算，熟记特殊角的三角函数值是解答本题的关键．
25．先化简，再求值：，其中．
【答案】；
【分析】先根据分式的混合运算化简，再根据特殊角的三角函数值的混合运算求得的值，代入化简结果进行计算即可求解．
【解析】解：
；
∵
∴原式．
【点睛】本题考查了分式的化简求值，特殊角的三角函数值，正确的计算是解题的关键．
26．用计算器求下列各式的值（精确到0.0001）：
(1)；
(2)；
(3)；
(4)．
【答案】(1)0.7314
(2)0.2164
(3)0.9041
(4)
【分析】利用计算器求出结果，根据有效数字的概念用四舍五入法取近似数即可．
【解析】（1）解：；
（2）解：；
（3）解：；
（4）解：．
【点睛】本题考查计算锐角三角函数值，熟练使用计算器是解题的关键．
27．用计算器求下列锐角三角函数值，并填入表中：
随着锐角A的度数不断增大，有怎样的变化趋势？呢？呢？你能说明自己的结论吗？
【答案】见解析，随着锐角A的度数不断增大，的值不断增大，的值不断减小，的值不断增大
【分析】利用计算器计算出各函数值，再观察表格由此得到答案．
【解析】解：
随着锐角A的度数不断增大，的值不断增大，的值不断减小，的值不断增大．
理由：在中，，假定的对边不变，当增大时，必有斜边减小，因此的值增大；假定的邻边不变，当增大时，必有斜边增大，对边增大，因此的值减小，的值增大．
【点睛】此题考查利用三角函数数值表求各角度的三角函数值，根据数据变化总结规律，熟记三角函数值的计算方法是解题的关键．
28．如图，在中，、、三边的长分别为、、，则，，．我们不难发现：，试探求、、之间存在的一般关系，并说明理由．

【答案】；，理由见解析
【分析】利用勾股定理可得，用，，表示正弦，余弦的平方和，即可得出；根据题意得出，即可得出．
【解析】存在的一般关系有：，，
证明：，，
，
，，
，
．
【点睛】本题考查了同角三角函数的关系，勾股定理的知识，熟练应用锐角三角函数关系是解答本题的关键．
29．嘉嘉在某次作业中得到如下结果：
，
，
，
，
．
据此，嘉嘉猜想：对于任意锐角，，若，均有．
(1)当，时，验证是否成立？
(2)嘉嘉的猜想是否成立？若成立，请结合如图所示给予证明，其中所对的边为，所对的边为，斜边为；若不成立，请举出一个反例；
(3)利用上面的证明方法，直接写出与，之间的关系．
【答案】(1)成立，见解析
(2)成立，见解析
(3)
【分析】（1）直接根据特殊角的三角函数值代入计算验证即可；
（2）根据正弦函数的定义列出，，结合勾股定理整理化简即可证得结论；
（3）根据正切函数的定义列出表达式，然后结合中，，，再变形代入整理即可得出结论．
【解析】（1）解：∵，，
∴，结论成立；
（2）解：成立．理由如下：
在中，，且，
∴，故结论成立；
（3）解：，理由如下：
在中，，，，
∴，
∴．
【点睛】本题考查余角之间的三角函数关系，以及同角三角函数关系的推理证明，理解三角函数的基本定义，灵活变形构造是解题关键．
锐角
ct
30°
45°
1
1
60°

锐角
…
…
…
锐角A
…
…
…
…
0.2588
0.3090
0.3420
0.3746
…
0.9848
0.9903
0.9945
…
…
0.9659
0.9511
0.9397
0.9272
…
0.1736
0.1392
0.1045
…
…
0.2679
0.3249
0.3640
0.4040
…
5.6713
7.1154
9.1544
…