



贵州省贵阳市2024-2025学年高一上学期10月联考数学试题
展开
这是一份贵州省贵阳市2024-2025学年高一上学期10月联考数学试题,文件包含贵阳市2027届高一年级联合考试一数学-答案docx、贵阳市2027届高一年级联合考试一数学-答案pdf、数学pdf等3份试卷配套教学资源,其中试卷共12页, 欢迎下载使用。
第Ⅰ卷(选择题,共58分)
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的选项中,只有一项是符合题目要求的)
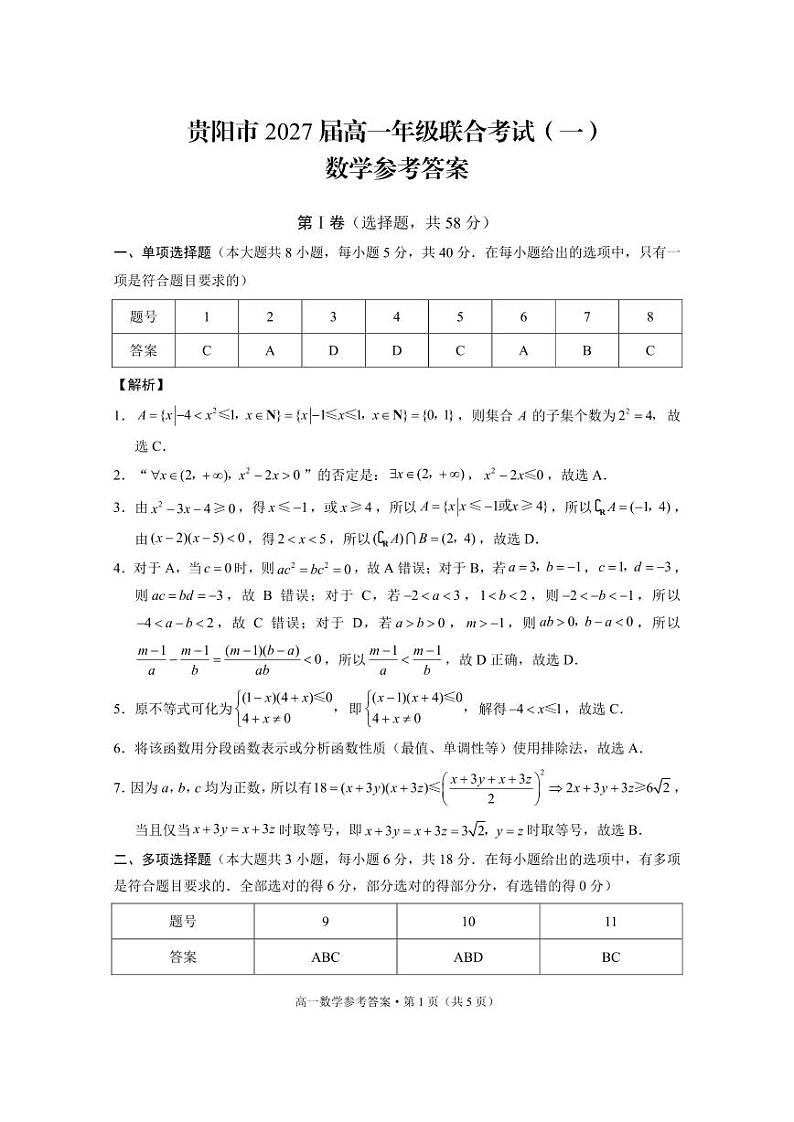
【解析】
1.,则集合A的子集个数为故选C.
2.“”的否定是:,,故选A.
3.由,得,或,所以,所以,由,得,所以,故选D.
4.对于A,当时,则,故A错误;对于B,若,,则,故B错误;对于C,若,,则,所以,故C错误;对于D,若,,则,所以,所以,故D正确,故选D.
5.原不等式可化为即解得,故选C.
6.将该函数用分段函数表示或分析函数性质(最值、单调性等)使用排除法,故选A.
7.因为a,b,c均为正数,所以有,当且仅当时取等号,即时取等号,故选B.
二、多项选择题(本大题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项是符合题目要求的.全部选对的得6分,部分选对的得部分分,有选错的得0分)
【解析】
9.首先分析方程没有正实数根时a的取值范围:当a=0时,方程为2x=1,方程有正实数根;当时,若方程有一个正,一非正的实根,则解得 若方程两个实数根均为正,则解得,综上,满足题意的a的取值范围是:,故选ABC.
10.C.设,则“”是“”的充分不必要条件,故选ABD.
11.A:,则,当且仅当时等号成立,错误;B:,当且仅当时等号成立,正确;C:,当且仅当时等号成立,正确;D:,则,当且仅当时等号成立,若有最小值不可能为2,错误,故选BC.
第Ⅱ卷(非选择题,共92分)
三、填空题(本大题共3小题,每小题5分,共15分)
【解析】
12.,进而求出,故答案为:.
13.由题可知,,因为,所以,解得,故答案为: .
14.,故答案为:7.
四、解答题(共77分.解答应写出文字说明,证明过程或演算步骤)
15.(本小题满分13分)
解:(1),……………………………………(2分)
当时,,…………………………………………………………(3分)
则或.……………………………………………………………(5分)
(2)因为,………………………………………(7分)
,
当,即时,……………………………………………………………(9分)
则,解得,…………………………………………………………(12分)
故实数的取值范围为.………………………………………………(13分)
16.(本小题满分15分)
解:(1)因为函数二次函数的零点为1,2,
所以,……………………………………………………………………(1分)
………………………………………………………………………(2分)
.…………………………………………………………………(3分)
又函数在取得最小值为,
而
…………………………………………………………(5分)
…………………………………………………………………………………(6分)
.……………………………………………………………………(7分)
(2)关于的不等式 .……………………(9分)
当时,不等式的解集为;……………………………………………………(11分)
当时,不等式的解集为;………………………………………………(13分)
当时,不等式的解集为.………………………………………………(15分)
17.(本小题满分15分)
解:(1)由结合基本不等式可得:
………………………………………………………………(2分)
又为正数,…………………………………………………(4分)
则,……………………………………………………………………(6分)
当且仅当,即时取等号.…………………………………………(7分)
(2)由可得,………………………………………………………(9分)
则,…………………………………(14分)
当且仅当,即时取等号.……………………………(15分)
18.(本小题满分17分)
解:(1)当时,;
………………………………………………………………………………………(3分)
当时,,
………………………………………………………………………………………(6分)
所以函数解析式为
……………………………………………………………………………………(8分)
(2)当时,因为,
又因为函数在上s随x的增大而增大,
所以当时,取最大值,;…………………………………(11分)
当时,
………………………………………………(15分)
当且仅当,即时等号成立,…………………………………(16分)
因为,所以时,的最大值为万元.
所以当年产量为29万台时,该公司获得最大利润万元.
……………………………………………………………………………………(17分)
19.(本小题满分17分)
解:(1)由得,………………………………………(1分)
∵存在,使得成立.
只需,……………………………………………………………………(4分)
解得或,……………………………………………………………………(6分)
所以实数a的取值范围为,或}.……………………………………(7分)
(2)由题意知对任意的恒成立,
即,…………………………………………………………………(9分)
,
……………………………………………………………………………………(13分)
又∵…………………………………………(15分)
当且仅当时取等号,………………………………………………………………(16分)
∴
所以实数的取值范围为.…………………………………………………(17分)题号
1
2
3
4
5
6
7
8
答案
C
A
D
D
C
A
B
C
题号
9
10
11
答案
ABC
ABD
BC
题号
12
13
14
答案
7
相关试卷
这是一份贵州省贵阳市清镇市博雅2024-2025学年第高一上学期第一次月考数学试题(无答案),共3页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份贵州省贵阳市2024-2025学年高三上学期8月摸底考试数学试题,文件包含贵州省贵阳市2025届高三年级8月摸底考试+数学答案pdf、贵州省贵阳市2024-2025学年第一学期25届高三年级八月摸底考试数学pdf等2份试卷配套教学资源,其中试卷共7页, 欢迎下载使用。
这是一份贵州省贵阳市普通中学2022-2023学年高一上学期期末监测数学试题,共15页。试卷主要包含了考试过程中不得使用计算器等内容,欢迎下载使用。









