

内蒙古赤峰市洪山区2024-2025学年九年级数学第一学期开学学业质量监测试题【含答案】
展开一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)
1、(4分)在直角三角形中,两条直角边的长分别为12和5,则斜边上的中线长是( )
A.6.5B.8.5C.13D.
2、(4分)直角三角形的面积为S,斜边上的中线长为d,则这个三角形周长为( )
A.B.C.D.
3、(4分)矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为( )
A.(3,1)B.(3,)C.(3,)D.(3,2)
4、(4分)函数的自变量x的取值范围是( )
A.x≠0B.x≠1C.x≥1D.x≤1
5、(4分)下列四组线段中,不能作为直角三角形三条边的是( )
A.8,15,17B.1,2,C.7,23,25D.1.5,2,2.5
6、(4分)若分式有意义,则实数的取值范围是( )
A.B.C.D.
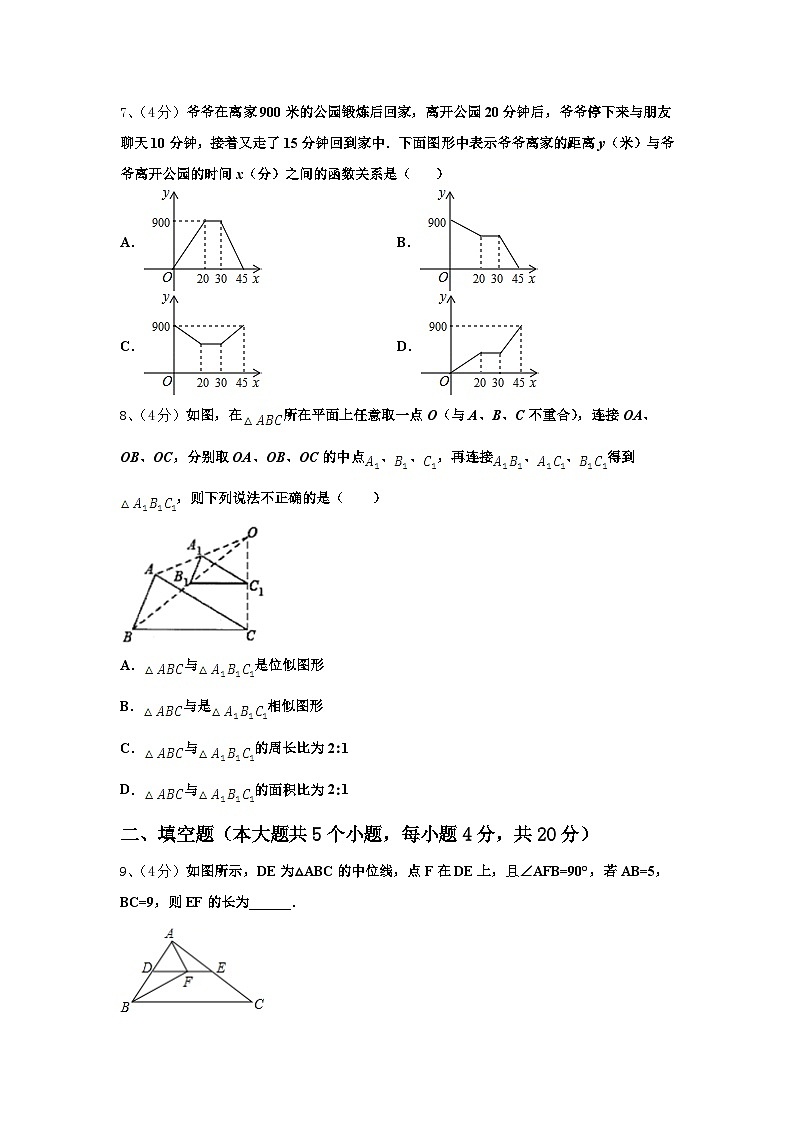
7、(4分)爷爷在离家900米的公园锻炼后回家,离开公园20分钟后,爷爷停下来与朋友聊天10分钟,接着又走了15分钟回到家中.下面图形中表示爷爷离家的距离y(米)与爷爷离开公园的时间x(分)之间的函数关系是( )
A.B.
C.D.
8、(4分)如图,在所在平面上任意取一点O(与A、B、C不重合),连接OA、OB、OC,分别取OA、OB、OC的中点、、,再连接、、得到,则下列说法不正确的是( )
A.与是位似图形
B.与是相似图形
C.与的周长比为2:1
D.与的面积比为2:1
二、填空题(本大题共5个小题,每小题4分,共20分)
9、(4分)如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=9,则EF的长为______.
10、(4分)如图,点A的坐标为,点B在直线上运动则线段AB的长度的最小值是___.
11、(4分)在平面直角坐标系中,点P(1,-3)关于原点O对称的点的坐标是________.
12、(4分)当m=_____时,是一次函数.
13、(4分)在直角三角形ABC中,∠B=90°,BD是AC边上的中线,∠A=30°,AB=5,则△ADB的周长为___________
三、解答题(本大题共5个小题,共48分)
14、(12分)如图,在平面直角坐标系中,点A的坐标为(﹣4,4),点B的坐标为(0,2).
(1)求直线AB的解析式;
(2)如图,以点A为直角顶点作∠CAD=90°,射线AC交x轴于点C,射线AD交y轴于点D.当∠CAD绕着点A旋转,且点C在x轴的负半轴上,点D在y轴的负半轴上时,OC﹣OD的值是否发生变化?若不变,求出它的值;若变化,求出它的变化范围.
15、(8分)在倡导“社会主义核心价值观”演讲比赛中,某校根据初赛成绩在七、八年级分别选出10名同学参加决赛,对这些同学的决赛成绩进行整理分析,绘制成如下团体成绩统计表和选手成绩折线统计图:
根据上述图表提供的信息,解答下列问题:
(1)请你把上面的表格填写完整;
(2)考虑平均数与方差,你认为哪个年级的团体成绩更好?
(3)假设在每个年级的决赛选手中分别选出2个参加决赛,你认为哪个年级的实力更强一些?请说明理由.
16、(8分)A、B两种机器人都被用来搬运化工原料,A型机器人比B型机器人每小时多搬运30kg,A型机器人搬运900kg与B型机器人搬运600kg所用时间相等,两种机器人每小时分别搬运多少化工原料?
17、(10分)如图是两个全等的直角三角形(和)摆放成的图形,其中,,点B落在DE边上,AB与CD相交于点F.若,求这两个直角三角形重叠部分的周长.
18、(10分)如图,在四边形中,,,,,,点从点出发,以的速度沿运动,点从点出发的同时,点从点出发,以的速度向点运动,当点到达点时,点也停止运动,设点、运动的时间为秒,从运动开始,当取何值时,?
B卷(50分)
一、填空题(本大题共5个小题,每小题4分,共20分)
19、(4分)方程的两个根是和,则的值为____.
20、(4分)已知点P(-2,1),则点P关于x轴对称的点的坐标是__.
21、(4分)如图,在平面直角坐标系中,矩形OABC的对角线AC平行于x轴,边OA与x轴正半轴的夹角为30°,OC=2,则点B的坐标是_______.
22、(4分)已知点A(﹣,a),B(3,b)在函数y=﹣3x+4的象上,则a与b的大小关系是_____.
23、(4分)如图,E是矩形ABCD的对角线的交点,点F在边AE上,且DF=DC,若∠ADF=25°,则∠ECD=___°.
二、解答题(本大题共3个小题,共30分)
24、(8分)某港口P位于东西方向的海岸线上.在港口P北偏东25°方向上有一座小岛A,且距离港口20海里;在港口与小岛的东部海域上有一座灯塔B,△PAB恰好是等腰直角三角形,其中∠B是直角;
(1)在图中补全图形,画出灯塔B的位置;(保留作图痕迹)
(2)一艘货船C从港口P出发,以每小时15海里的速度,沿北偏西20°的方向航行,请求出1小时后该货船C与灯塔B的距离.
25、(10分)如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=BC,连接CD和EF.
(1)求证:DE=CF;
(2)求EF的长.
26、(12分)某县教育局为了了解学生对体育立定跳远()、跳绳()、掷实心球()、中长跑()四个项目的喜爱程度(每人只选一项),确定中考体育考试项目,特对八年级某班进行了调查,并绘制成如下频数、频率统计表和扇形统计图:
(1)求出这次调查的总人数;
(2)求出表中的值;
(3)若该校八年级有学生1200人,请你算出喜爱跳绳的人数,并发表你的看法.
参考答案与详细解析
一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)
1、A
【解析】
利用勾股定理求得直角三角形的斜边,然后利用直角三角形斜边上的中线等于斜边的一半解题.
【详解】
如图,在△ABC中,∠C=90°,AC=12,BC=1
则根据勾股定理知,AB==13
∵CD为斜边AB上的中线
∴CD=AB=6.1.
故选:A.
本题考查了勾股定理、直角三角形斜边上的中线.勾股定理:如果直角三角形两直角边分别为a,b,斜边为c,那么a2+b2=c2.即直角三角形,两直角边的平方和等于斜边的平方.直角三角形的性质:在直角三角形中斜边上的中线等于斜边的一半.
2、C
【解析】
根据直角三角形的性质求出斜边长,根据勾股定理、完全平方公式计算即可.
【详解】
设直角三角形的两条直角边分别为x、y,
斜边上的中线为d,
斜边长为2d,
由勾股定理得,,
直角三角形的面积为S,
,
则,
则,
,
这个三角形周长为:,
故选C.
【点睛】本题考查了勾股定理的应用,解题的关键是根据直角三角形的两条直角边长分别是a,b,斜边长为c,得出.
3、B
【解析】
试题分析:如图,作点D关于直线AB的对称点H,连接CH与AB的交点为E,此时△CDE的周长最小.
∵D(,0),A(3,0),∴H(,0),∴直线CH解析式为y=﹣x+4,当x=3时,y=,∴点E坐标(3,)
故选B.
考点:1矩形;2轴对称;3平面直角坐标系.
4、B
【解析】
根据题意若函数y=有意义,可得x-1≠0;
解得x≠1;故选B
5、C
【解析】
根据勾股定理的逆定理逐一判断即可.
【详解】
A.因为 82+152=172,故以8,15,17为三边长能构成直角三角形,故本选项不符合题意;
B. 12+22=()2,故以1,2,为三边长能构成直角三角形,故本选项不符合题意;
C. 72+232≠252,故以7,23,25为三边长不能构成直角三角形,故本选项符合题意;
D. ,故以为三边长能构成直角三角形,故本选项不符合题意.
故选C.
此题考查的是直角三角形的判定,掌握用勾股定理的逆定理判定直角三角形是解决此题的关键.
6、B
【解析】
分式有意义,则,求出x的取值范围即可.
【详解】
∵分式有意义,
∴,
解得:,
故选B.
本题是对分式有意义的考查,熟练掌握分式有意义的条件是解决本题的关键.
7、B
【解析】
由题意,爷爷在公园回家,则当时,;从公园回家一共用了45分钟,则当时,;
【详解】
解:由题意,爷爷在公园回家,则当时,;
从公园回家一共用了分钟,则当时,;
结合选项可知答案B.
故选:B.
本题考查函数图象;能够从题中获取信息,分析运动时间与距离之间的关系是解题的关键.
8、D
【解析】
根据三角形中位线定理得到A1B1=AB,A1C1=AC,B1C1=BC,根据位似变换的概念、相似三角形的性质判断即可.
【详解】
∵点A1、B1、C1分别是OA、OB、OC的中点,
∴A1B1=AB,A1C1=AC,B1C1=BC,
∴△ABC与△A1B1C1是位似图形,A正确;
△ABC与是△A1B1C1相似图形,B正确;
△ABC与△A1B1C1的周长比为2:1,C正确;
△ABC与△A1B1C1的面积比为4:1,D错误;
故选:D.
考查的是位似变换,掌握位似变换的概念、相似三角形的性质是解题的关键.
二、填空题(本大题共5个小题,每小题4分,共20分)
9、1
【解析】
利用直角三角形斜边上的中线等于斜边的一半,可求出DF的长,再利用三角形的中位线平行于第三边,并且等于第三边的一半,可求出DE的长,进而求出EF的长
【详解】
解:∵∠AFB=90°,D为AB的中点,
∴DF=AB=1.5,
∵DE为△ABC的中位线,
∴DE=BC=4.5,
∴EF=DE-DF=1,
故答案为:1.
本题考查了直角三角形斜边上的中线性质:在直角三角形中,斜边上的中线等于斜边的一半和三角形的中位线性质:三角形的中位线平行于第三边,并且等于第三边的一半.
10、
【解析】
当线段AB最短时,直线AB与直线垂直,根据勾股定理求得AB的最短长度.
【详解】
解:当线段AB最短时,直线AB与直线垂直,
过点A作直线l,
因为直线是一、三象限的角平分线,
所以,
所以,
所以,
,即,
所以.
故答案是:.
考查了垂线段最短的性质,一次函数图象上点的坐标特征,勾股定理的应用,熟知垂线段最短是解题的关键.
11、(﹣1,3)
【解析】
根据平面直角坐标系中任意一点P(x,y),关于原点的对称点是(-x,-y),然后直接作答即可.
【详解】
根据中心对称的性质,可知:点P(1,−3)关于原点O中心对称的点P`的坐标为(−1,3).
故答案为:(﹣1,3).
此题考查关于原点对称的点的坐标,解题关键在于掌握其性质.
12、3或0
【解析】
根据一次函数的定义即可求解.
【详解】
依题意得m-3≠0,2m+1=1或m-3=0,
解得m=0或m=3,
故填:3或0.
此题主要考查一次函数的定义,解题的关键是熟知一次函数的特点.
13、
【解析】
先作出Rt△ABC,根据∠A=30°,AB=5,可求得BC、 AC的长度,然后根据直角三角形斜边中线等于斜边的一半求出中线BD的长度,继而可求得△ADB的周长.
【详解】
解:如图所示,
∵∠ABC=90°,∠A=30°,AB=5,
∴设BC=x,则AC=2x
∵
∴
∴x=5
∴BC=5,AC=10
在直角三角形ABC中,∠ABC==90°,BD是AC边上的中线
∴
∴△ADB的周长为:
故答案为:
本题考查了勾股定理、含30°角的直角三角形和直角三角形斜边的中线等知识,解答本题的关键是根据勾股定理求出直角边的长度.
三、解答题(本大题共5个小题,共48分)
14、(1);(2)不变,值为2.
【解析】
(1)由、两点的坐标利用待定系数法可求得直线的解析式;
(2)过分别作轴和轴的垂线,垂足分别为、,可证明,可得到,从而可把转化为,再利用线段的和差可求得.
【详解】
解:(1)设直线的解析式为:.
点,点在直线上,
,
解得.
直线的解析式为:;
(2)不变.
理由如下:
过点分别作轴、轴的垂线,垂足分别为、,如图1.
则,
又,
,
,
,
,
.
,
.
在和中,
,
,
.
.
故的值不发生变化,值为2.
考查了一次函数综合题,涉及知识点有待定系数法、全等三角形的判定和性质等.在(1)中注意待定系数法的应用步骤,在(2)中构造三角形全等是解题的关键.本题考查知识点较多,综合性较强,难度适中.
15、(1)八年级成绩的平均数1.7,七年级成绩的众数为80,八年级成绩的众数为1;
(2)八年级团体成绩更好些;
(3)七年级实力更强些.
【解析】
(1)通过读图即可,即可得知众数,再根据图中数据即可列出求平均数的算式,列式计算即可.
(2)根据方差的意义分析即可.
(3)分别计算两个年级前两名的总分,得分较高的一个班级实力更强一些.
【详解】
解:(1)由折线统计图可知:
七年级10名选手的成绩分别为:80,87,89,80,88,99,80,77,91,86;
八年级10名选手的成绩分别为:1,97,1,87,1,88,77,87,78,88;
八年级平均成绩=(1+97+1+87+1+88+77+87+78+88)=1.7(分),
七年级成绩中80分出现的次数最多,所以七年级成绩的众数为80;
八年级成绩中1分出现的次数最多,所以八年级成绩的众数为1.
(2)由于七、八年级比赛成绩的平均数一样,而八年级的方差小于七年级的方差,方差越小,则其稳定性越强,所以应该是八年级团体成绩更好些;
(3)七年级前两名总分为:99+91=190(分),
八年级前两名总分为:97+88=11(分),
因为190分>11分,所以七年级实力更强些.
本题考查了折线统计图,此题要求同学们不但要看懂折线统计图,而且还要掌握方差、平均数、众数的运用.
16、A型机器人每小时搬运kg化工原料,B型机器人每小时搬运kg化工原料.
【解析】
设B种机器人每小时搬运x千克化工原料,则A种机器人每小时搬运(x+30)千克化工原料,根据A型机器人搬运900kg原料所用时间与B型机器人搬运600kg原料所用时间相等,列方程进行求解即可.
【详解】
设B型机器人每小时搬运kg化工原料,则A型机器人每小时搬运kg化工原料,由题意得,
,
解此分式方程得:,
经检验是分式方程的解,且符合题意,
当时,,
答:A型机器人每小时搬运kg化工原料,B型机器人每小时搬运kg化工原料.
本题考查了列分式方程解实际问题的运用,分式方程的解法的运用,解答时根据A型机器人搬运900kg原料所用时间与B型机器人搬运600kg原料所用时间相等建立方程是关键.
17、
【解析】
根据全等三角形的性质得出BC=EC,∠ABC=∠E=60°,求出△BCE是等边三角形,求出∠DCB=30°,∠BFC=90°,解直角三角形求出BF和CF,即可求出答案.
【详解】
解:如图
∵,,
∴,,
∴是等边三角形,
∴,
又∵,
∴,
又∵,在中,
∴,,
∴的周长是.
本题考查了全等三角形的性质,含30°角的直角三角形的性质,等边三角形的性质和判定,求出BF和CF的长是解此题的关键.
18、当时,
【解析】
首先判定当时,四边形PDCQ是平行四边形,然后利用其性质PD=QC,构建方程,即可得解.
【详解】
当时,四边形PDCQ是平行四边形,
此时PD=QC,
∴
∴
∴当时,.
此题主要考查利用平行四边形的性质构建方程,即可解题.
一、填空题(本大题共5个小题,每小题4分,共20分)
19、
【解析】
根据韦达定理求解即可.
【详解】
∵方程的两个根是和
∴由韦达定理得
故答案为:.
本题考查了一元二次方程根的问题,掌握韦达定理是解题的关键.
20、 (-2,-1)
【解析】
根据关于x轴对称的点的横坐标相等,纵坐标互为相反数,可得答案.
【详解】
点P(﹣2,1),则点P关于x轴对称的点的坐标是(﹣2,﹣1),
故答案是:(﹣2,﹣1).
考查了关于x轴对称的对称点,利用关于x轴对称的点的横坐标相等,纵坐标互为相反数是解题关键.
21、(2,2).
【解析】
解:过点B作DE⊥OE于E,
∵矩形OABC的对角线AC平行于x轴,边OA与x轴正半轴的夹角为30°,
∴∠CAO=30°.
又∵OC=2,∴AC=1.∴OB=AC=1.
又∵∠OBC=∠CAO=30°,DE⊥OE,∠CBA=90°,∴∠OBE=30°.
∴OE=2,BE=OB·cs∠OBE=2.
∴点B的坐标是(2,2).
故答案为:(2,2).
22、a>b
【解析】
根据k<0,y随x增大而减小解答
【详解】
解:∵k=﹣3<0,
∴y随x的增大而减小,
∵﹣<3,
∴a>b.
故答案为:a>b.
此题主要考查了一次函数的图像上点的坐标特征,利用一次函数的增减性求解更简便
23、17.1.
【解析】
根据矩形的性质由∠ADF求出∠CDF,再由等腰三角形的性质得出∠ECD即可.
【详解】
解:∵四边形ABCD是矩形,
∴∠ADC=90°,
∵∠ADF=21°,
∴∠CDF=∠ADC﹣∠ADF=90°﹣21°=61°,
∵DF=DC,
∴∠ECD=,
故答案为:17.1.
本题考查了矩形的性质,等腰三角形的性质,解本题的关键是求出∠CDF.是一道中考常考的简单题.
二、解答题(本大题共3个小题,共30分)
24、(1)如图,点B即为所求见解析;(2)出发1小时后,货船C与灯塔B的距离为5海里.
【解析】
(1)轨迹题意画出图形即可;
(2)首先证明∠CPB=90°,求出PB、PC利用勾股定理即可解决问题;
【详解】
(1)如图,点B即为所求
(2)如图,∠CPN=20°,∠NPA=25°,
∠APB=45°,∠CPB=90°
在Rt△ABP中,∵AP=20,BA=BP,
∴PB=10
在Rt△PCB中,由勾股定理得,
CB===5,
∴出发1小时后,货船C与灯塔B的距离为5海里.
此题是一道方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.
25、见解析;
【解析】
试题分析:(1)直接利用三角形中位线定理得出DEBC,进而得出DE=FC;
(2)利用平行四边形的判定与性质得出DC=EF,进而利用等边三角形的性质以及勾股定理得出EF的长
试题解析:(1)证明:∵D、E分别为AB、AC的中点, ∴DEBC,
∵延长BC至点F,使CF=BC, ∴DEFC, 即DE=CF;
(2)解:∵DEFC, ∴四边形DEFC是平行四边形, ∴DC=EF,
∵D为AB的中点,等边△ABC的边长是2, ∴AD=BD=1,CD⊥AB,BC=2, ∴DC=EF=.
考点:三角形中位线定理;等边三角形的性质;平行四边形的判定与性质
26、(1)60;(2) ;(3)240人,看法见解析
【解析】
(1)用C科目人数除以其所占比例;
(2)根据频数=频率×总人数求解可得;
(3)总人数乘以样本中B科目人数所占比例,根据图表得出正确的信息即可.
【详解】
解:(1)这次调查的总人数为6÷(36÷360)=60(人);
(2)a=60×0.5=30(人);b=12÷60=0.2;c=6÷60=0.1;d=0.2×60=12(人);
(3)喜爱跳绳的人数为1200×0.2=240(人),
由扇形统计图知喜爱立定跳远的人数占总人数的一半,是四个学科中人数最多的科目.
本题考查了扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.用到的知识点为:总体数目=部分数目÷相应百分比.
题号
一
二
三
四
五
总分
得分
批阅人
七年级
八年级
平均数
85.7
_______
众数
_______
_______
方差
37.4
27.8
内蒙古自治区赤峰市翁牛特旗第一中学2024年九年级数学第一学期开学学业质量监测试题【含答案】: 这是一份内蒙古自治区赤峰市翁牛特旗第一中学2024年九年级数学第一学期开学学业质量监测试题【含答案】,共20页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
内蒙古自治区赤峰市2024-2025学年数学九年级第一学期开学学业水平测试模拟试题【含答案】: 这是一份内蒙古自治区赤峰市2024-2025学年数学九年级第一学期开学学业水平测试模拟试题【含答案】,共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
内蒙古赤峰市洪山区2025届九上数学开学检测模拟试题【含答案】: 这是一份内蒙古赤峰市洪山区2025届九上数学开学检测模拟试题【含答案】,共19页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












