山东省济南市市中学区育英中学2025届九年级数学第一学期开学综合测试试题【含答案】

这是一份山东省济南市市中学区育英中学2025届九年级数学第一学期开学综合测试试题【含答案】，共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）下列各组数中，可以构成直角三角形的三边长的是（ ）
A．1，2，3B．2，3，4C．1，，D．1，，3
2、（4分）某校在开展“节约每一滴水”的活动中，从八年级的100名同学中任选20名同学汇总了各自家庭一个月的节水情况，将有关数据（每人上报节水量都是整数）整理如表：
请你估计这100名同学的家庭一个月节约用水的总量大约是（ ）
A．180tB．230tC．250tD．300t
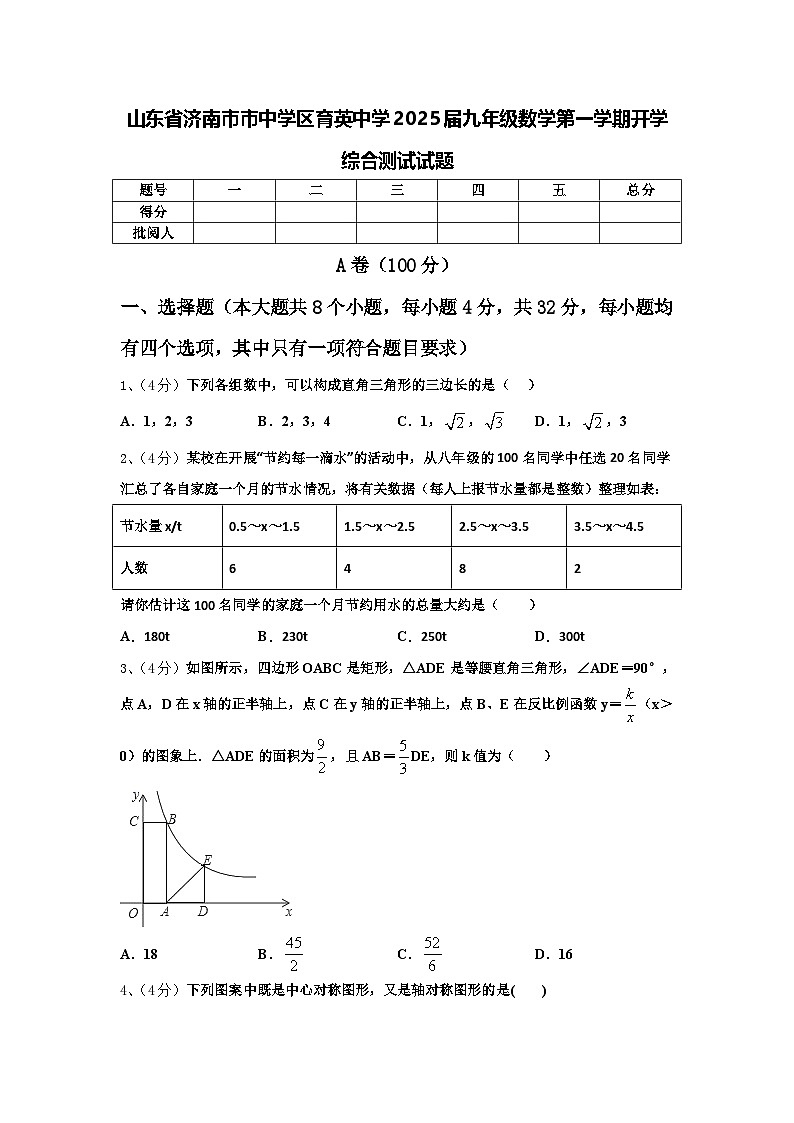
3、（4分）如图所示，四边形OABC是矩形，△ADE是等腰直角三角形，∠ADE＝90°，点A，D在x轴的正半轴上，点C在y轴的正半轴上，点B、E在反比例函数y＝（x＞0）的图象上．△ADE的面积为，且AB＝DE，则k值为（ ）
A．18B．C．D．16
4、（4分）下列图案中既是中心对称图形，又是轴对称图形的是( )
A．B．
C．D．
5、（4分）小亮在同一直角坐标系内作出了和的图象，方程组的解是( )
A．B．C．D．
6、（4分）下列交通标志图案中，是中心对称图形的是（ ）
A．B．C．D．
7、（4分）如图，小“鱼”与大“鱼”是位似图形，如果小“鱼”上一个“顶点”的坐标为（a，b），那么大“鱼”上对应“顶点”的坐标为（ ）．
A．（－a，－2b）B．（－2a，－b）C．（－2a，－2b）D．（－2b，－2a）
8、（4分）下列电视台的台标，是中心对称图形的是（ ）
A．B．C．D．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）《九章算术》是中国古代的数学专著，它奠定了中国古代数学的基本框架，以计算为中心，密切联系实际，以解决人们生产、生活中的数学问题为目的．书中记载了这样一个问题：“今有句五步，股十二步．问句中容方几何．”其大意是：如图，Rt△ABC的两条直角边的长分别为5和12，则它的内接正方形CDEF的边长为_____．
10、（4分）计算_________.
11、（4分）分解因式b2（x﹣3）+b（x﹣3）＝_____．
12、（4分）当a＝＋1，b＝－1时，代数式的值是________．
13、（4分）如图，在△ABC中，∠B=∠C=60°，点D在AB边上，DE⊥AB，并与AC边交于点E．如果AD=1，BC=6，那么CE等于______．
三、解答题（本大题共5个小题，共48分）
14、（12分）如图，在△ABC中，BD、CE分别为AC、AB边上的中线，BD、CE交于点H，点G、F分别为HC、HB的中点，连接AH、DE、EF、FG、GD，其中HA＝BC．
（1）证明：四边形DEFG为菱形；
（2）猜想当AC、AB满足怎样的数量关系时，四边形DEFG为正方形，并说明理由．
15、（8分）反比例函数y1=（x＞0）的图象与一次函数y2=﹣x+b的图象交于A，B两点，其中A（1，2）
（1）求这两个函数解析式；
（2）在y轴上求作一点P，使PA+PB的值最小，并直接写出此时点P的坐标．
16、（8分）新能源汽车投放市场后，有效改善了城市空气质量。经过市场调查得知，某市去年新能源汽车总量已达到3250辆，预计明年会增长到6370辆.
（1）求今、明两年新能源汽车数量的平均增长率；
（2）为鼓励市民购买新能源汽车，该市财政部门决定对今年增加的新能源汽车给予每辆0.8万元的政府性补贴.在（1）的条件下，求该市财政部门今年需要准备多少补贴资金？
17、（10分）如图，在△ABC中，BD平分∠ABC，∠A=2∠C．
（1）若∠C=38°，则∠ABD= ；
（2）求证：BC=AB+AD；
（3）求证：BC2=AB2+AB•AC．
18、（10分）端午节假期，某商场开展促销活动，活动规定：若购买不超过100元的商品，则按全额交费；若购买超过100元的商品，则超过100元的部分按8折交费.设商品全额为x元，交费为y元.
（1）写出y与x之间的函数关系式.
（2）某顾客在-一次消费中，向售货员交纳了300元，那么在这次消费中，该顾客购买的商品全额为多少元？
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）直线y＝k1x+b与直线y＝k2x+c在同一平面直角坐标系中的图象如图所示，则关于X的不等式 k1x+b＞k2x+c的解集为_____．
20、（4分）化简：=_______________.
21、（4分）在△ABC中，AB＝12，AC＝5，BC＝13，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF中点，则PM的最小值为_____．
22、（4分）现用甲、乙两种汽车将吨防洪物资运往灾区，甲种汽车载重吨，乙种汽车载重吨，若一共安排辆汽车运送这些物资，则甲种汽车至少应安排 _________辆.
23、（4分）若的整数部分是a，小数部分是b，则______.
二、解答题（本大题共3个小题，共30分）
24、（8分）已知直线分别交x轴于点A、交y轴于点
求该直线的函数表达式；
求线段AB的长．
25、（10分）如图，已知菱形ABCD中，对角线AC、BD相交于点O，过点C作CE∥BD，过点D作DE∥AC，CE与DE相交于点E．
(1)求证：四边形CODE是矩形；
(2)若AB＝5，AC＝6，求四边形CODE的周长．
26、（12分）如图，经过点B（0，2）的直线y＝kx+b与x轴交于点C，与正比例函数y＝ax的图象交于点A（﹣1，3）
（1）求直线AB的函数的表达式；
（2）直接写出不等式（kx+b）﹣ax＜0的解集；
（3）求△AOC的面积；
（4）点P是直线AB上的一点，且知△OCP是等腰三角形，写出所有符合条件的点P的坐标．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、C
【解析】
根据勾股定理的逆定理，判断三角形是否为直角三角形，需要验证三角形三边关系，两小边长的平方和等于最长边的平方即可．
【详解】
A．，不能构成直角三角形，此选项错误；
B．，不能构成直角三角形，此选项错误；
C．，能构成直角三角形，此选项正确；
D．，不能构成直角三角形，此选项错误；
故选：C．
考查了勾股定理的逆定理，利用三角形三边关系判定三角形是否为直角三角形，用到实数平方的计算，熟记定理内容，注意判定时，边长是平方关系．
2、B
【解析】
利用组中值求平均数可得：选出20名同学家的平均一个月节约用水量= =2.3，
∴估计这100名同学的家庭一个月节约用水的总量大约是=2.3×100=230t．
故选B.
3、B
【解析】
设B（m，5），则E（m+3，3），因为B、E在y＝上，则有5m＝3m+9＝k，由此即可解决问题；
【详解】
解：∵△ADE是等腰直角三角形，面积为，
∴AD＝DE＝3，
∵AB＝DE，
∴AB＝5，设B（m，5），则E（m+3，3），
∵B、E在y＝上，
则有5m＝3m+9＝k
∴m＝，
∴k＝5m＝.
故选B．
本题考查反比例函数系数k的几何意义，等腰直角三角形的性质等知识，解题的关键是学会利用参数解决问题，属于中考常考题型．
4、C
【解析】
判断轴对称的关键是寻找对称轴，两边图象折叠后可重合，判断中心对称是要寻找对称中心，旋转180度后重合
A、是轴对称图形，不是中心对称图形，故错误；
B、是轴对称图形，不是中心对称图形，故错误；
C、是轴对称图形，又是中心对称图形，故正确；
D、是轴对称图形，不是中心对称图形，故错误．
故选C．
5、B
【解析】
由数形结合可得，直线和的交点即为方程组
的解，可得答案.
【详解】
解：由题意得：直线和的交点即为方程组
的解，可得图像上两直线的交点为（-2，2），
故方程组的解为，
故选B.
本题主要考查了函数解析式与图象的关系,满足解析式的点就在函数的图象上,在函数的图象上的点,就一定满足函数解析式.函数图象交点坐标为两函数解析式组成的方程组的解.
6、C
【解析】
根据中心对称图形的概念，分别判断即可.
【详解】
解：A、B、D不是中心对称图形，C是中心对称图形.
故选C.
点睛：本题考查了中心对称图形的概念：中心对称图形是要寻找对称中心，旋转180度后与原图重合．
7、C
【解析】
根据位似图形的性质结合图形写出对应坐标即可．
【详解】
∵小“鱼”与大“鱼”的位似比是
∴大“鱼”上对应“顶点”的坐标为（－2a，－2b）
故答案为：C．
本题考查了位似图形的问题，掌握位似图形的性质是解题的关键．
8、D
【解析】
根据中心对称图形的概念，中心对称图形是图形沿对称中心旋转180度后与原图重合，因此，四个选项中只有D符合。故选D。
二、填空题（本大题共5个小题，每小题4分，共20分）
9、
【解析】
根据正方形的性质得：DE∥BC，则△ADE∽△ACB，列比例式可得结论．
【详解】
∵四边形CDEF是正方形，AC=5，BC=12，
∴CD=ED，DE∥CF，
设ED=x，则CD=x，AD=5-x，
∵DE∥CF，
∴∠ADE=∠C，∠AED=∠B，
∴△ADE∽△ACB，
∴，
∴，
解得：x=，
故答案为．
此题考查了相似三角形的判定和性质、正方形的性质，设未知数，构建方程是解题的关键．
10、19+6
【解析】
根据完全平方公式展开计算即可。
【详解】
解：18+6+1=19+6
本题考查了用完全平方公式进行实数的计算，理解和掌握乘法公式是关键。
11、b（x﹣3）（b+1）
【解析】
用提公因式法分解即可.
【详解】
原式= b（x﹣3）·b+b（x﹣3）＝b（x﹣3）（b+1）.
故答案为：b（x﹣3）（b+1）
本题考查了因式分解，把一个多项式化成几个整式的乘积的形式，叫做因式分解.因式分解常用的方法有：①提公因式法；②公式法；③十字相乘法；④分组分解法. 因式分解必须分解到每个因式都不能再分解为止.
12、
【解析】
分析：根据已知条件先求出a+b和a﹣b的值，再把要求的式子进行化简，然后代值计算即可．
详解：∵a=﹣1，∴a+b=+1+﹣1=2，a﹣b=+1﹣+1=2，∴====．
故答案为．
点睛：本题考查了分式的值，用到的知识点是完全平方公式、平方差公式和分式的化简，关键是对给出的式子进行化简．
13、4
【解析】
根据等边三角形的性质和含30°的直角三角形的性质解答即可．
【详解】
∵在△ABC中,∠B=∠C=60°，
∴∠A=60°，
∵DE⊥AB，
∴∠AED=30°，
∵AD=1，
∴AE=2，
∵BC=6，
∴AC=BC=6，
∴CE=AC−AE=6−2=4.
故答案为4.
本题考查了等边三角形的性质，解题的关键是熟练的掌握等边三角形的性质.
三、解答题（本大题共5个小题，共48分）
14、（1）证明见解析；（2）当AC＝AB时，四边形DEFG为正方形，证明见解析
【解析】
（1）利用三角形中位线定理推知ED∥FG，ED＝FG，则由“对边平行且相等的四边形是平行四边形”证得四边形DEFG是平行四边形，同理得EF＝HA＝BC＝DE，可得结论；
（2）AC＝AB时，四边形DEFG为正方形，通过证明△DCB≌△EBC（SAS），得HC＝HB，证明对角线DF＝EG，可得结论．
【详解】
（1）证明：∵D、E分别为AC、AB的中点，
∴ED∥BC，ED＝BC．
同理FG∥BC，FG＝BC，
∴ED∥FG，ED＝FG，
∴四边形DEFG是平行四边形，
∵AE＝BE，FH＝BF，
∴EF＝HA，
∵BC＝HA，
∴EF＝BC＝DE，
∴▱DEFG是菱形；
（2）解：猜想：AC＝AB时，四边形DEFG为正方形，
理由是：∵AB＝AC，
∴∠ACB＝∠ABC，
∵BD、CE分别为AC、AB边上的中线，
∴CD＝AC，BE＝AB，
∴CD＝BE，
在△DCB和△EBC中，
∵
∴△DCB≌△EBC（SAS），
∴∠DBC＝∠ECB，
∴HC＝HB，
∵点G、F分别为HC、HB的中点，
∴HG＝HC，HF＝HB，
∴GH＝HF，
由（1）知：四边形DEFG是菱形，
∴DF＝2FH，EG＝2GH，
∴DF＝EG，
∴四边形DEFG为正方形．
故答案为（1）证明过程见解析；（2）当AC＝AB时，四边形DEFG为正方形.
本题考查了平行四边形、矩形的判定、菱形的判定、正方形的判定、三角形的中位线性质定理，三角形中线的性质及等腰三角形的性质，其中三角形的中位线的性质定理为证明线段相等和平行提供了依据．
15、（1）y1=；y2=﹣x+3；（2）点P（0，）．
【解析】
将已知点A分别代入反比例函数和一次函数里，即可求出k、b，再将k、b的值代入两个函数里，就可以求出两个函数的解析式；
作A点关于y轴的对称点，并与B连接这条线段即为所求。根据已知求出B点坐标，再求出新线的解析式，最后求出P点坐标．
【详解】
（1）将点A（1，2）代入y1=，得：k=2，
则y1=；
将点A（1，2）代入y2=﹣x+b，得：﹣1+b=2，
解得：b=3，
则y2=﹣x+3；
（2）作点A关于y轴的对称点A′（﹣1，2），连接A′B，交y轴于点P，即为所求，
如图所示：
由得：或，
∴B（2，1），
设A′B所在直线解析式为y=mx+n，
根据题意，得：，
解得：，
则A′B所在直线解析式为y=3x﹣5，
当x=0时，y=，
所以点P（0，）．
函数解析式．
16、（1）40%；（2）财政部门今年需要准备1040万元补贴资金.
【解析】
（1）设今、明两年新能源汽车数量的平均增长率为x，根据“去年新能源汽车总量已达到3250辆，预计明年会增长到6370辆”列出方程并解答；
（2）根据（1）中的增长率可以得到：3250×增长率×0.1．
【详解】
解：（1）设今、明两年新能源汽车数量的平均增长率为，由题意得
.
解得，，（舍）
因此，.
所以，今、明两年新能源汽车数量的平均增长率为40%.
（2）3250×40%×0.1=1040（万元）.
所以，财政部门今年需要准备1040万元补贴资金.
本题考查一元二次方程的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程，再求解．
17、（1）33°；（1）证明见解析.（3）证明见解析.
【解析】
试题分析：（1）在BC上截取BE=AB，利用“边角边”证明△ABD和△BED全等，根据全等三角形对应边相等可得DE=AD，全等三角形对应角相等可得∠AED=∠A，然后求出∠C=∠CDE，根据等角对等边可得CE=DE，然后结合图形整理即可得证；
（1）由（1）知：△ABD≌△BED，根据全等三角形对应边相等可得DE=AD，全等三角形对应角相等可得∠AED=∠A，然后求出∠C=∠CDE，根据等角对等边可得CE=DE，等量代换得到EC=AD，即得答案BC=BE+EC=AB+AD；
（3）为了把∠A=1∠C转化成两个角相等的条件，可以构造辅助线：在AC上取BF=BA，连接AE，根据线段的垂直平分线的性质以及三角形的内角和定理的推论能够证明AB=F．再根据勾股定理表示出BC1，AB1．再运用代数中的公式进行计算就可证明．
试题解析：（1）在BC上截取BE=BA，如图1，
在△ABD和△BED中，
,
∴△ABD≌△BED，
∴∠BED=∠A，
∵∠C=38°，∠A=1∠C，
∴∠A=76°，
∴∠ABC=180°﹣∠C﹣∠A=66°，
BD平分∠ABC，
∴∠ABD=33°；
（1）由（1）知：△ABD≌△BED，
∴BE=AB，DE=AD，∠BED=∠A，
又∵∠A=1∠C，
∴∠BED=∠C+∠EDC=1∠C，
∴∠EDC=∠C，
∴ED=EC，
∴EC=AD
∴BC=BE+EC=AB+AD；t
（3）如图1，过B作BG⊥AC于G，
以B为圆心，BA长为半径画弧，交AC于F，
则BF=BA，
在Rt△ABG和Rt△GBG中，
，
∴Rt△ABG≌Rt△GBG，
∴AG=FG，
∴∠BFA=∠A，
∵∠A=1∠C，
∴∠BFA=∠FBC+∠C=1∠C，
∴∠FBC=∠C，
∴FB=FC，
FC=AB，
在Rt△ABG和Rt△BCG中，
BC1=BG1+CG1，
AB1=BG1+AG1
∴BC1﹣AB1=CG1﹣AG1=（CG+AG）（CG﹣AG）
=AC（CG﹣GF）=AC•FC
=AC•AB．
18、（1）；（2）该顾客购买的商品全额为350元.
【解析】
（1）根据题意分段函数，即当自变量x≤100和x＞100两种情况分别探索关系式，
（2）根据金额，判断符合哪个函数，代入求解即可．
【详解】
（1）
（2）由题意得，
解得．
答：该顾客购买的商品全额为350元.
考查根据实际问题求一次函数的关系式、分段函数关系式的探索，以及代入求值等知识，体会函数的意义．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、x＞1
【解析】
根据图形，找出直线 k1x+b在直线k2x+c上方部分的x的取值范围即可．
【详解】
解：由图形可知，当x＞1时，k1x+b＞k2x+c，
所以，不等式的解集是x＞1．
故答案为x＞1．
本题考查了两直线相交的问题，根据函数图象在上方的函数值比函数图象在下方的函数值大，利用数形结合求解是解题的关键．
20、
【解析】
分析：首先将分式的分子和分母进行因式分解，然后进行约分化简得出答案．
详解：原式=．
点睛：本题主要考查的是分式的化简问题，属于基础题型．学会因式分解是解决这个问题的关键．
21、
【解析】
根据题意可证△ABC是直角三角形，则可以证四边形AEPF是矩形，可得AP=EF，根据直角三角形斜边上中线等于斜边一半，可得AP=EF=2PM，则AP值最小时，PM值最小，根据垂线段最短，可求AP最小值，即可得PM的最小值．
【详解】
解：连接AP，
∵AB2+AC2＝169，BC2＝169
∴AB2+AC2＝BC2
∴∠BAC＝90°，且PE⊥AB，PF⊥AC
∴四边形AEPF是矩形
∴AP＝EF，∠EPF＝90°
又∵M是EF的中点
∴PM＝EF
∴当EF值最小时，PM值最小，即当AP值最小时，PM值最小．
根据垂线段最短，即当AP⊥BC时AP值最小
此时S△ABC＝AB×AC＝BC×AP
∴AP＝
∴EF＝
∴PM＝
故答案为
本题考查了矩形的判定与性质，勾股定理逆定理，以及垂线段最短，关键是证EF=AP
22、6
【解析】
设甲种汽车安排x辆，则乙种汽车安排10-x辆, 根据两辆汽车载重不少于46吨建立不等式求出其解，即可得出答案.
【详解】
解：设甲种汽车安排x辆，则乙种汽车安排10-x辆，根据题意可得：5x+4(10-x)≥46
解得：x≥6
因此甲种汽车至少应安排6辆.
本题主要考查了一元一次不等式的应用，关键是以载重不少于46吨作为不等量关系列出方程求解.
23、1.
【解析】
若的整数部分为a，小数部分为b，
∴a=1，b=，
∴a-b==1．
故答案为1．
二、解答题（本大题共3个小题，共30分）
24、（1）；（2）AB=．
【解析】
把B点坐标代入中求出b即可；
先利用一次函数解析式确定A点坐标，然后利用勾股定理计算出AB的长．
【详解】
解：把代入得，
所以该直线的函数表达式为；
当时，，解得，则，
所以AB的长．
本题考查了待定系数法求一次函数解析式：先设出函数的一般形式，如求一次函数的解析式时，先设；将自变量x的值及与它对应的函数值y的值代入所设的解析式，得到关于待定系数的方程或方程组；解方程或方程组，求出待定系数的值，进而写出函数解析式．
25、 (1)证明见解析；（2）14.
【解析】
试题分析：（1）先证明四边形CODE是平行四边形，再利用菱形的性质得到直角，证明四边形CODE是矩形．（2）由勾股定理可知OD长，OC是AC一半，所以可知矩形的周长.
试题解析：
（1）∵ CE∥BD，DE∥AC，
∴ 四边形CODE是平行四边形，
∵ 四边形ABCD是菱形，∴ AC⊥BD，
∴ ∠DOC＝90°，∴ □ CODE是矩形；
（2）在菱形ABCD中，OC＝AC＝×6＝3，CD＝AB＝5，
在Rt△COD中，OD＝，
∴ 四边形CODE的周长即矩形CODE的周长为：2（OD＋OC）＝2×（4＋3）＝14.
26、（2）y＝﹣x+2．（2）x＜﹣2.（3）3；（4）（2，2）或（0，2）或P（2+，﹣）或（2﹣，）．
【解析】
（2）利用待定系数法即可解决问题；
（2）观察图象写出直线y＝kx+b的图象在直线y＝ax的图象下方的自变量的取值范围即可；
（3）求出点C坐标，利用三角形的面积公式计算即可；
（4）分三种情形分别讨论求解即可解决问题；
【详解】
解：（2）依题意得：，
解得，
∴所求的一次函数的解析式是y＝﹣x+2．
（2）观察图形可知：不等式（kx+b）﹣ax＜0的解集；
x＜﹣2．
（3）对于y＝﹣x+2，令y＝0，得x＝2
∴C（2，0），
∴OC＝2．
∴S△AOC＝×2×3＝3．
（4）
①当点P与B重合时，OP2＝OC，此时P2（0，2）；
②当PO＝PC时，此时P2在线段OC的垂直平分线上，P2（2，2）；
③当PC＝OC＝2时，设P（m．﹣m+2），
∴（m﹣2）2+（﹣m+2）2＝4，
∴m＝2±，
可得P3（2﹣，），P4（2+，﹣），
综上所述，满足条件的点P坐标为：（2，2）或（0，2）或P（2+，﹣）或（2﹣，）．
本题考查一次函数综合题、一元一次不等式的解、等腰三角形的判定和性质等知识，解题的关键是学会用分类讨论的思想思考问题，属于中考压轴题．
题号
一
二
三
四
五
总分
得分
批阅人
节水量x/t
0.5～x～1.5
1.5～x～2.5
2.5～x～3.5
3.5～x～4.5
人数
6
4
8
2