山东省济宁市梁山县街道第一中学2024年九上数学开学质量跟踪监视试题【含答案】

这是一份山东省济宁市梁山县街道第一中学2024年九上数学开学质量跟踪监视试题【含答案】，共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
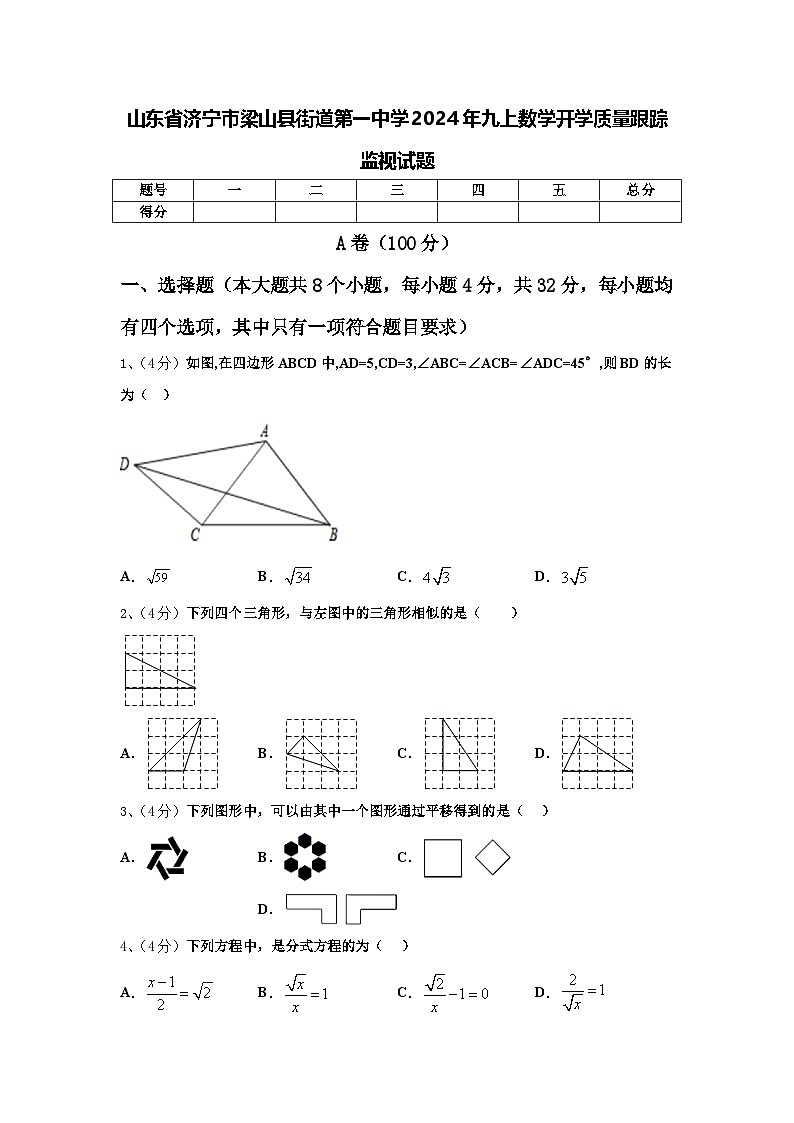
1、（4分）如图,在四边形ABCD中,AD=5,CD=3,∠ABC=∠ACB=∠ADC=45°,则BD的长为（ ）
A．B．C．D．
2、（4分）下列四个三角形，与左图中的三角形相似的是（ ）
A．B．C．D．
3、（4分）下列图形中，可以由其中一个图形通过平移得到的是（ ）
A．B．C．D．
4、（4分）下列方程中，是分式方程的为（ ）
A．B．C．D．
5、（4分）一个三角形的三边分别是6、8、10，则它的面积是（ ）
A．24B．48C．30D．60
6、（4分）如图，△AOB为等腰三角形，顶点A的坐标（2，），底边OB在x轴上．将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B，点A的对应点A′在x轴上，则点O′的坐标为（ ）
A．（，）B．（，）C．（，）D．（，4）
7、（4分）计算的值为（ ）
A．9B．1C．4D．0
8、（4分）如图,中，点是边的中点，交对角线于点，则等于( )
A．B．C．D．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图，一次函数的图象与x轴、y轴分别交于点A、B，将沿直线AB翻折得到，连接OC，那么线段OC的长为______．
10、（4分）如图，△ABC中，D，E分别 是边AB，AC的中点．若DE=2，则BC= ．
11、（4分）数据2，4，3，x，7，8，10的众数为3，则中位数是_____．
12、（4分）如果a2-ka+81是完全平方式，则k=________．
13、（4分）一次函数的图象经过点，且与轴、轴分别交于点、，则的面积等于___________．
三、解答题（本大题共5个小题，共48分）
14、（12分）如图，在中，点为边的中点，点在内，平分点在上，．
（1）求证：四边形是平行四边形；
（2）线段之间具有怎样的数量关系？证明你所得到的结论．
15、（8分）如图，在中，对角线BD平分，过点A作，交CD的延长线于点E，过点E作，交BC延长线于点F．
（1）求证：四边形ABCD是菱形；
（2）若求EF的长．
16、（8分）在学习一元一次不等式与一次函数中，小明在同一个坐标系中分别作出了一次函数和的图象，分别与x轴交于点A、B，两直线交于点C． 已知点，，观察图象并回答下列问题：
（1）关于x的方程的解是______；关于x的不等式的解集是______；
（2）直接写出关于x的不等式组的解集；
（3）若点，求关于x的不等式的解集和△ABC的面积．
17、（10分）计算：
（1） ；
（2）（﹣1）（+1）+（﹣2）2
18、（10分）如图，直线分别与轴、轴交于两点，与直线交于点.
（1）点坐标为（ ， ），B为（ ， ）.
（2）在线段上有一点，过点作轴的平行线交直线于点，设点的横坐标为，若四边形是平行四边形时，求出此时的值.
（3）若点为轴正半轴上一点，且，则在轴上是否存在一点，使得四个点能构成一个梯形若存在，求出所有符合条件的点坐标；若不存在，请说明理由.
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）函数与的图象恰有两个公共点，则实数的取值范围是_______.
20、（4分）若正多边形的每一个内角为，则这个正多边形的边数是__________．
21、（4分）计算：的结果是__________．
22、（4分）平面直角坐标系xOy中，点A（x1，y1）与B（x2，y2），如果满足x1+x2＝0，y1﹣y2＝0，其中x1≠x2，则称点A与点B互为反等点．已知：点C（3，8）、G（﹣5，8），联结线段CG，如果在线段CG上存在两点P，Q互为反等点，那么点P的横坐标xP的取值范围是__．
23、（4分）一次函数的图像在轴上的截距是__________.
二、解答题（本大题共3个小题，共30分）
24、（8分）先化简，再求值：，其中a＝6
25、（10分）某货运公司有大小两种货车,3辆大货车与4辆小货车一次可以运货29吨,2辆大货车与6辆小货车一次可以运货31吨.
(1)1辆大货车和1辆小货车一次可以分别运货多少吨?
(2)有46.4吨货物需要运输,货运公司拟安排大小货车共10辆(要求两种货车都要用),全部货物一次运完,其中每辆大货车一次运货花费500元,每辆小货车一次运货花费300元,请问货运公司应如何安排车辆最节省费用?
26、（12分）如图，在平面直角坐标系中，点是原点，四边形是菱形，点的坐标为，点在轴的负半轴上，直线与轴交于点，与轴交于点．
（1）求直线的解析式；
（2）动点从点出发，沿折线方向以1个单位/秒的速度向终点匀速运动，设的面积为，点的运动时间为秒，求与之间的函数关系式．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、A
【解析】
根据等式的性质，可得∠BAD与∠CAD′的关系，根据SAS，可得△BAD与△CAD′的关系，根据全等三角形的性质，可得BD与CD′的关系，根据勾股定理，可得答案．
【详解】
作AD′⊥AD,AD′=AD,连接CD′,DD′,如图：
∵∠BAC+∠CAD=∠DAD′+∠CAD，
即∠BAD=∠CAD′，
在△BAD与△CAD′中，

∴△BAD≌△CAD′(SAS)，
∴BD=CD′.
∠DAD′=90∘
由勾股定理得DD′=，
∠D′DA+∠ADC=90∘
由勾股定理得CD′=，
∴BD=CD′= ，
故选：A.
此题考查勾股定理，解题关键在于作辅助线
2、B
【解析】
设单位正方形的边长为1，求出各边的长，再根据各选项的边长是否成比例关系即可判断.
【详解】
设单位正方形的边长为1，给出的三角形三边长分别为2，4，2．
A、三角形三边分别是2，，3，与给出的三角形的各边不成比例，故A选项错误；
B、三角形三边，2，，与给出的三角形的各边成比例，故B选项正确；
C、三角形三边2，3，，与给出的三角形的各边不成比例，故C选项错误；
D、三角形三边，，4，与给出的三角形的各边不成正比例，故D选项错误．
故选：B．
本题主要应用两三角形相似的判定定理，三边对应成比例，做题即可．
3、B
【解析】
根据平移的定义直接判断即可．
【详解】
解：由其中一个图形平移得到整个图形的是B，
故选：B．
此题主要考查了图形的平移，把一个图形整体沿某一直线方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同，图形的这种移动叫做平移．注意平移是图形整体沿某一直线方向移动．
4、C
【解析】
根据分式方程的定义：分母里含有字母的方程叫做分式方程进行判断．
【详解】
A. 是整式方程，故选项错误；
B. 是整式方程，故选项错误；
C. 分母中含有未知数x，所以是分式方程，故选项正确；
D. 是整式方程，故选项错误.
故选C.
此题考查分式方程的判定，掌握分式方程的定义是解题的关键.
5、A
【解析】
先根据勾股定理逆定理证明三角形是直角三角形,再利用面积法代入求解即可．
【详解】
∵,
∴三角形是直角三角形,
∴面积为:．
故选A．
本题考查勾股定理逆定理的应用,关键在于熟悉常用的勾股数．
6、C
【解析】
利用等面积法求O'的纵坐标，再利用勾股定理或三角函数求其横坐标．
【详解】
解：过O′作O′F⊥x轴于点F，过A作AE⊥x轴于点E，
∵A的坐标为（1，），∴AE=，OE=1．
由等腰三角形底边上的三线合一得OB=1OE=4，
在Rt△ABE中，由勾股定理可求AB=3，则A′B=3，
由旋转前后三角形面积相等得，即，
∴O′F=．
在Rt△O′FB中，由勾股定理可求BF=，∴OF=．
∴O′的坐标为（）．
故选C．
本题考查坐标与图形的旋转变化；勾股定理；等腰三角形的性质；三角形面积公式．
7、B
【解析】
原式第一项利用绝对值定义计算,第二项利用零指数幂法则计算,最后一项利用负整数指数幂法则计算即可得到结果.
【详解】
原式=4+1-4=1
故选B
此题考查了实数的运算,熟练掌握运算法则是解本题的关键.
8、B
【解析】
如图，证明AD∥BC，AD=BC；得到△DEF∽△BCF，进而得到；证明BC=AD=2DE，即可解决问题．
【详解】
四边形为平行四边形，
；
，
；
点是边的中点，
，
．故选B．
该题主要考查了平行四边形的性质、相似三角形的判定及其性质等几何知识点及其应用问题；牢固掌握平行四边形的性质、相似三角形的判定及其性质是关键．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、.
【解析】
利用一次函数图象上点的坐标特征求得点A、B的坐标，易得线段AB的长度，然后利用面积法求得OD的长度，结合翻折图形性质得到．
【详解】
解：如图，设直线OC与直线AB的交点为点D，
一次函数的图象与x轴、y轴分别交于点A、B，
、，
，，，
将沿直线AB翻折得到，
，
，
．
故答案是：．
考查了一次函数图象与几何变换，此题将求线段OC的长度转换为求直角三角形AOB斜边上高的问题，降低了题目的难度．
10、1.
【解析】
试题分析：根据题意画出图形，再由三角形的中位线定理进行解答即可．
试题解析：∵△ABC中，D、E分别是△ABC的边AB、AC的中点，DE=2
∴DE是△ABC的中位线，
∴BC=2DE=2×2=1．
考点：三角形中位线定理．
11、1
【解析】
先根据众数是一组数据中出现次数最多的数据，求得x，再由中位数要把数据按从小到大的顺序排列，位于最中间的一个数（或两个数的平均数）为中位数．
【详解】
解：∵这组数据2，1，3，x，7，8，10的众数为3，
∴x＝3，
从小到大排列此数据为：2，3，3，1，7，7，10，
处于中间位置的数是1，
∴这组数据的中位数是1；
故答案为：1．
本题主要考查数据统计中的众数和中位数的计算，关键在于根据题意求出未知数.
12、±18.
【解析】
利用完全平方公式的结构特征判断即可确定出k的值．
【详解】
∵二次三项式a2-ka+81是完全平方式，
∴k=±18，
故答案为：±18.
此题考查完全平方式，解题关键在于掌握运算法则
13、
【解析】
∵一次函数y=−2x+m的图象经过点P(−2,3)，
∴3=4+m，
解得m=−1，
∴y=−2x−1，
∵当x=0时，y=−1，
∴与y轴交点B(0,−1)，
∵当y=0时,x=−，
∴与x轴交点A(−,0)，
∴△AOB的面积：×1×=.
故答案为.
点睛：首先根据待定系数法求得一次函数的解析式，然后计算出与x轴交点，与y轴交点的坐标，再利用三角形的面积公式计算出面积即可．
三、解答题（本大题共5个小题，共48分）
14、（1）见详解；（2）,证明见详解.
【解析】
（1）延长CE交AB于点G，证明，可得，结合题目条件利用中位线中的平行即可求证；
（2）根据已知条件易得，根据全等可得，从而得到之间的数量关系.
【详解】
（1）延长CE交AB于点G，如图所示：
∵平分
∴
在中
∵点为边的中点
∴
∴DE为的中位线
∴
∵
∴四边形是平行四边形
（2）∵四边形是平行四边形
∴
∵D、E分别是BC、GC的中点
本题考查了平行四边形的判定和性质，全等三角形的性质，中位线的性质等知识点，解题的关键在于判断四边形是平行四边形，DE为的中位线，，从而可解此题.
15、 (1)见解析；(2)
【解析】
（1）证明，得出，即可得出结论；
（2）由菱形的性质得出，证明四边形ABDE是平行四边形，，得出，在中，由等腰直角三角形的性质和勾股定理即可求出EF的长．
【详解】
（1）证明：∵四边形ABCD是平行四边形，
，
∵BD平分，
，
，
，
是菱形；
（2）解：∵四边形ABCD是菱形，
，
，
∴四边形ABDE是平行四边形，，
，
，
，
是等腰直角三角形，
．
本题考查了平行四边形的性质与判定、菱形的判定与性质、等腰三角形的判定以及等腰直角三角形的判定与性质；熟练掌握菱形判定与性质是解决问题的关键．
16、 (1)x=-1，；（2）-1＜x＜2；（3），．
【解析】
（1）利用直线与x轴交点即为y=0时，对应x的值，进而得出答案；
（2）利用两直线与x轴交点坐标，结合图象得出答案；
（3）两条直线相交于点C，根据点C的左右两边图像的位置可确定答案；利用三角形面积公式求得即可．
【详解】
解：（1）∵一次函数y=k1x+b1和y=kx+b的图象，分别与x轴交于点A（-1，0）、B（2，0），
∴关于x的方程k1x+b1=0的解是x=-1，
关于x的不等式kx+b＜0的解集，为x＞2，
故答案为x=-1，x＞2；
（2）根据图象可以得到关于x的不等式组的解集-1＜x＜2；
（3）∵C(1, 3)，
根据图象可以得到关于x的不等式k1x+b1>kx+b的解集：
∵AB=3，
∴S△ABC=AB•yC=×3×3=．
此题主要考查了一元一次方程的解、一次函数与不等式，一次函数与不等式组，三角形面积，正确利用数形结合解题是解题关键．
17、 (1);(2)8-
【解析】
（1）根据二次根式的混合运算法则进行计算即可.
（2）利用完全平方公式和平方差公式进行计算即可.
【详解】
（1）原式＝3++2﹣
＝3+2+
＝；
（2）原式＝2﹣1+3﹣4+4
＝8﹣4．
此题考查二次根式的混合运算，解题关键在于利用平方差公式和完全平方公式进行计算.
18、（1）点的坐标是，点的坐标是；（2）；（3）符合条件的点坐标为
【解析】
（1）先将点C坐标代入直线l1中，求出直线l1的解析式，令x=0和y=0，即可得出结论；
（2）先求出直线l2的解析式，表示出点E，F的坐标，在判断出OB=EF，建立方程求解，即可得出结论；
（3）先求出点P的坐标，分两种情况求出直线PQ，AQ的解析式，即可得出结论．
【详解】
解:（1）∵点C（2，）在直线l1：上，
∴，
∴直线l1的解析式为，
令x=0，∴y=3，∴B（0，3），
令y=0，∴，∴x=4，∴A（4，0），
故答案为：点的坐标是，点的坐标是.
（2）∵轴，点的横坐标为，∴点的横坐标也为，
∵直线与直线交于点
∵点是直线的一点，
∴点E的坐标是，
∵点是直线上的一点，
∴点的坐标是
∵当
（3）若点为轴正半轴上一点，，，
∴，.
当时
直线AB的解析式为：
直线PQ的解析式为
∴点的坐标是
当时
直线BP的解析式为，
直线AQ的解析式为
∴点的坐标是
综上，在平面直角坐标系中存在点，使得四个点能构成一个梯形，符合条件的点坐标为
此题是一次函数综合题，主要考查了待定系数法，平行四边形的性质，三角形的面积公式，利用方程的思想解决问题是解本题的关键．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、或
【解析】
画图象用数形结合解题，y=m|x|的图在x轴上过原点是折线，关于y轴对称；m>0时，y=x+m斜率为1，与y=m|x|交于第一、二象限，m0时，过第一、二象限，y=x+a斜率为1，m>0时，过第一、二、三象限，若使其图象恰有两个公共点，必有m>1；
②m