

山东省日照市东港区新营中学2024-2025学年八年级上学期月考数学试卷(10月份)
展开1.(3分)如图,把手机放在一个支架上面,就可以非常方便地使用,这里所用的几何原理是( )
A.两点之间线段最短B.垂线段最短
C.两点确定一条直线D.三角形具有稳定性
2.(3分)已知三条线段的长分别是3,7,m,若它们能构成三角形,则整数m的最大值是( )
A.11B.10C.9D.7
3.(3分)在△ABC和△DEF中,下列条件不能判断这两个三角形全等的是( )
A.∠A=∠D,BC=EF,AB=DE
B.∠A=∠D,AB=DE,AC=DF
C.AB=DE,AC=DF,BC=EF
D.∠C=∠F=90°,AB=DE,AC=DF
4.(3分)如图所示的网格由边长相同的小正方形组成,点A,B,C,D,E,F,G均在小正方形的顶点上,则△ABC的重心是( )
A.点GB.点DC.点ED.点F
5.(3分)具备下列条件的△ABC中,不是直角三角形的是( )
A.∠A+∠B=∠CB.∠A:∠B:∠C=1:2:3
C.∠A﹣∠B=90°D.
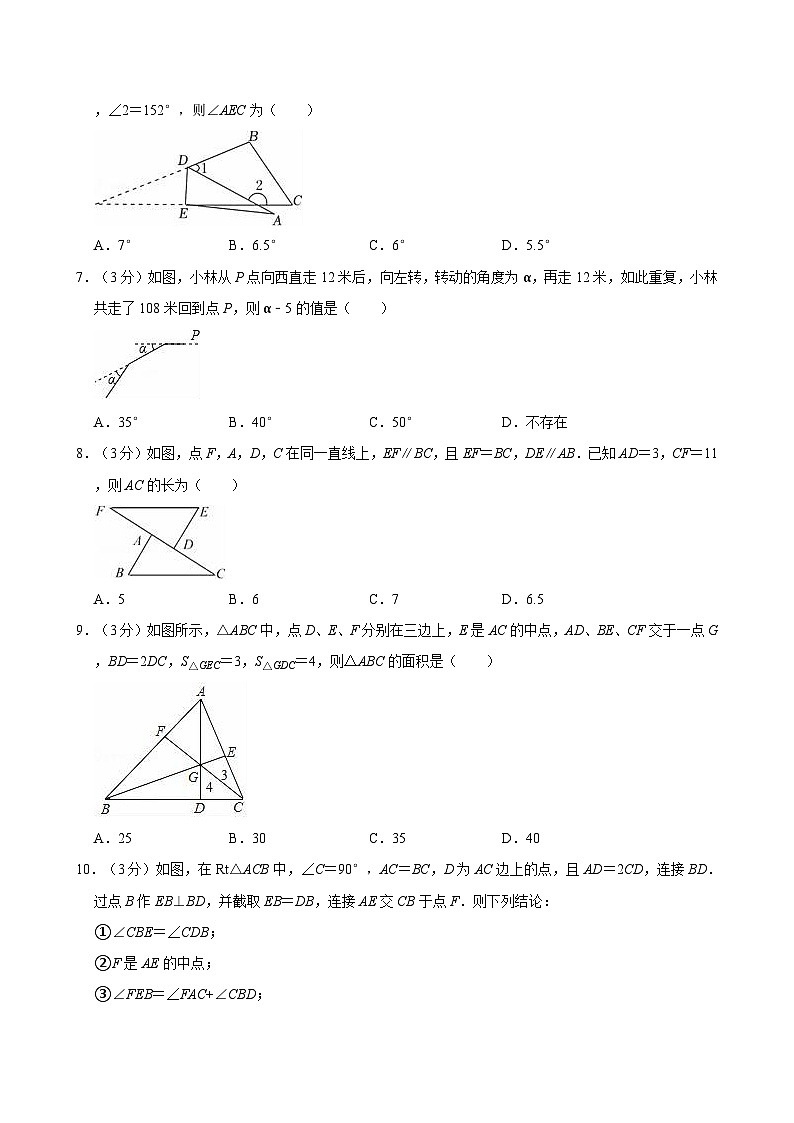
6.(3分)如图,将三角形纸片ABC沿DE折叠,当点A落在四边形BCED的外部时,测量得∠1=50°,∠2=152°,则∠AEC为( )
A.7°B.6.5°C.6°D.5.5°
7.(3分)如图,小林从P点向西直走12米后,向左转,转动的角度为α,再走12米,如此重复,小林共走了108米回到点P,则α﹣5的值是( )
A.35°B.40°C.50°D.不存在
8.(3分)如图,点F,A,D,C在同一直线上,EF∥BC,且EF=BC,DE∥AB.已知AD=3,CF=11,则AC的长为( )
A.5B.6C.7D.6.5
9.(3分)如图所示,△ABC中,点D、E、F分别在三边上,E是AC的中点,AD、BE、CF交于一点G,BD=2DC,S△GEC=3,S△GDC=4,则△ABC的面积是( )
A.25B.30C.35D.40
10.(3分)如图,在Rt△ACB中,∠C=90°,AC=BC,D为AC边上的点,且AD=2CD,连接BD.过点B作EB⊥BD,并截取EB=DB,连接AE交CB于点F.则下列结论:
①∠CBE=∠CDB;
②F是AE的中点;
③∠FEB=∠FAC+∠CBD;
④BF=3CF.其中正确的结论共有( )
A.1个B.2个C.3个D.4个
二、填空题(本题共6小题,每小题3分,共18分.)
11.(3分)若一个多边形的边数是这个多边形从一个顶点引出的对角线条数的2倍,则这个多边形是 边形.
12.(3分)如图,∠A+∠B+∠C+∠D+∠E+∠F等于 .
13.(3分)如图,在△ABC中,AD是高线,AE、BF是角平分线,它们相交于点O,∠BAC=50°,∠C=70°,∠EAD度数为 .
14.(3分)如图,小明与小敏玩跷跷板游戏,支点O是跷跷板的中点,两人分别坐在跷跷板两端(即OF=OG),如果点O至地面的距离是50cm,当小敏从水平位置CD下降40cm,这时小明离地面的高度是 .
15.(3分)如图,∠ABD、∠ACD的角平分线交于点P,若∠A=50°,∠D=10°,则∠P的度数为 .
16.(3分)如图,CA⊥AB,垂足为点A,射线BM⊥AB,垂足为点B,AB=15cm,AC=6cm.动点E从A点出发以3cm/s的速度沿射线AN运动,动点D在射线BM上,随着E点运动而运动,始终保持ED=CB.若点E的运动时间为t秒(t>0),则当t= 秒时,△DEB与△BCA全等.
三、解答题(本题共8小题,共72分.第17-18题每题6分,第19-20题每题8分,第21-22题每题10分,第23-24题每题12分,解答应写出文字说明、证明过程或演算步骤.)
17.(6分)如图,在△ABC中,AB>AC,AD为BC边上的中线.
(1)S△ABD S△ACD(填“>”、“<”或“=”);
(2)若△ABD的周长比△ACD的周长多4,且AB+AC=14,求AB,AC的长.
18.(6分)阅读小明和小红的对话,解决下列问题.
(1)这个“多加的锐角”是 度.
(2)小明求的是几边形内角和?
(3)若这是个正多边形,则这个正多边形的一个内角是多少度?
19.(8分)如图,点D,E分别在AB,AC上,BD=CE,AB=AC,BE,CD相交于点O.
求证:∠B=∠C.
小刚同学的证明过程如下:
(1)小刚同学的证明过程中,第 步出现错误;
(2)请写出正确的证明过程.
20.(8分)如图,已知A,D,C,E在同一直线上,BC和DF相交于点O,AD=CE,AB∥DF,AB=DF.
(1)求证:△ABC≌△DFE;
(2)连接CF,若∠BCF=54°,∠DFC=20°,求∠DFE的度数.
21.(10分)如图,AC⊥BC,DC⊥EC,AC=BC,DC=EC,AE与BD交于点F.
求证:AE=BD.
22.(10分)定义:如果一个三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形”.
(1)若△ABC是“准互余三角形”,∠C>90°,∠A=56°,则∠B= °;
(2)若△ABC是直角三角形,∠ACB=90°.
①如图,若AD是∠BAC的角平分线,请你判断△ABD是否为“准互余三角形”?并说明理由.
②点E是边BC上一点,△ABE是“准互余三角形”,若∠B=28°,求∠AEB的度数.
23.(12分)通过对下面数学模型的研究学习,解决下列问题:
【模型呈现】
某兴趣小组在从汉代数学家赵爽的弦图(如图1,由外到内含三个正方形)中提炼出两个三角形全等模型图(如图2、图3),即“一线三等角”模型和“K字”模型.
【问题发现】
(1)如图2,已知,△ABC中,CA=CB,∠ACB=90°,一直线过顶点C,过A,B分别作其垂线,垂足分别为E,F.求证:EF=AE+BF;
(2)如图3,若改变直线的位置,其余条件与(1)相同,请直接写出EF,AE,BF之间的数量关系 ;
【问题提出】
(3)在(2)的条件下,若EF=4AE,EF=5,则△BFC的面积为 .
(4)如图4,四边形ABCD中,∠ABC=∠CAB=∠ADC=45°,△ADC面积为18且CD的长为9,则△BCD的面积为 .
24.(12分)数学兴趣小组在活动时,老师提出了这样一个问题:如图1,在△ABC中,AB=6,AC=10,D是BC的中点,求BC边上的中线AD的取值范围.
【方法探索】(1)小明在组内经过合作交流,得到了如下的解决方法:如图1,延长AD到点E,使DE=AD,连接BE.根据SAS可以判定△ADC≌△EDB,得出AC=BE.这样就能把线段AB、AC、2AD集中在△ABE中.利用三角形三边的关系,即可得出中线AD的取值范围是 .
【问题解决】(2)由第(1)问方法的启发,请解决下面问题:如图2,在△ABC中,D是BC边上的一点,AE是△ABD的中线,CD=AB,∠BDA=∠BAD,试说明:AC=2AE;
【问题拓展】(3)如图3,AD是△ABC的中线,过点A分别向外作AE⊥AB、AF⊥AC,使得AE=AB,AF=AC,判断线段EF与AD的关系,并说明理由.
2024-2025学年山东省日照市东港区新营中学八年级(上)月考数学试卷(10月份)
参考答案与试题解析
一、单项选择题(本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.【解答】解:把手机放在一个支架上面,就可以非常方便地使用,这里所用的几何原理是:手机支架具有三角形的稳定性.
故选:D.
2.【解答】解:∵三条线段的长分别是3,7,m,它们能构成三角形,
∴7﹣3<m<7+3,
∴4<m<10,
∴整数m的最大值是9.
故选:C.
3.【解答】解:A、利用SSA,不能判断两个三角形全等,符合题意;
B、利用SAS,得到两个三角形全等,不符合题意;
C、利用SSS,得到两个三角形全等,不符合题意;
D、利用HL,得到两个三角形全等,不符合题意.
故选:A.
4.【解答】解:取BC的中点N,取AC的中点M,连接AN,BM,如图所示,
则AN与BM的交点为D,
故点D是△ABC的重心,
故选:B.
5.【解答】解:∵∠A+∠B+∠C=180°,
当∠A+∠B=∠C时,则∠C+∠C=180°,
∴∠C=90°,
故选项A中的条件,能使△ABC为直角三角形,不符合题意;
∵∠A:∠B:∠C=1:2:3
∴可设∠A=α,∠B=2α,∠C=3α,
∵∠A+∠B+∠C=180°,
∴α+2α+3α=180°,
解得:α=30°,
∴∠C=3α=90°,
故选项B中的条件,能使△ABC为直角三角形,不符合题意;
∵∠A﹣∠B=90°,
∴∠A=90°+∠B>90°,
∴△ABC为钝角三角形,
故选项C中的条件,不能使△ABC为直角三角形,符合题意;
∵∠A=∠B=∠C,∠A+∠B+∠C=180°,
∴∠C+∠C+∠C=180°,
∴∠C=90°,
故选项D中的条件,能使△ABC为直角三角形,不符合题意.
故选:C.
6.【解答】解:∵∠1=50°,∠2=152°,
∴∠B+∠C=360°﹣∠1﹣∠2=360°﹣50°﹣152°=158°,
∴∠A=180°﹣(∠B+∠C)=180°﹣158°=22°,
∴∠A+∠AEC=180°﹣∠2,
即22°+∠AEC=180°﹣152°,
∴∠AEC=6°.
故选:C.
7.【解答】解:设边数为n,根据题意,
n=108÷12=9,
∴α=360°÷9=40°.
所以α﹣5=35°,
故选:A.
8.【解答】解:∵EF∥BC,
∴∠F=∠C,
∵DE∥AB,
∴∠EDF=∠BAC,
∵EF=BC,
∴△ABC≌△DEF(AAS),
∴AC=FD,
∴CD=AF,
∵AD=3,CF=11,
∴CD+AF=CF﹣AD=8,
∴CD=4,
∴AC=AD+CD=4+3=7.
故选:C.
9.【解答】解:BD=2DC,
∴S△ABD=2S△ACD,
∴S△ABC=3S△ACD,
∵E是AC的中点,
∴S△AGE=S△CGE,
又∵S△GEC=3,S△GDC=4,
∴S△ACD=S△AGE+S△CGE+S△CGD=3+3+4=10,
∴S△ABC=3S△ACD=3×10=30.
故选:B.
10.【解答】解:过点E作EH⊥BC,垂足为H,
∴∠BHE=∠FHE=90°,
∵EB⊥BD,
∴∠DBE=90°,
∴∠DBC+∠CBE=90°,
∵∠C=90°,
∴∠DBC+∠CDB=90°,
∴∠CDB=∠CBE;
∵EB=DB,∠BHE=∠C=90°,
∴△CDB≌△HBE(AAS),
∴CD=BH,BC=HE,∠CBD=∠BEH,
∵BC=AC,
∴HE=AC,
∵∠C=∠FHE=90°,∠AFC=∠EFH,
∴△AFC≌△EFH(AAS),
∴CF=FH,AF=EF,∠FAC=∠FEH,
∴点F是AE的中点;
∵∠FEB=∠FEH+∠BEH,
∴∠FEB=∠FAC+∠CBD;
故①②③都正确;
∵AC=BC,CD=BH,
∴AC﹣CD=BC﹣BH,
∴AD=CH,
∵AD=2CD,
∴CH=2BH,
∵CH=2CF=2FH,
∴BH=FH=CF,
∴BF=2CF,
故④不正确;
所以,上列结论,其中正确的结论共有3个,
故选:C.
二、填空题(本题共6小题,每小题3分,共18分.)
11.【解答】解:设此多边形有n条边,由题意,
得n=2(n﹣3),
解得n=6,
∴这个多边形是六边形.
故答案为:六.
12.【解答】解:∵∠A+∠F=180°﹣∠ANF,
∠B+∠C=180°﹣∠BHC,
∠E+∠D=180°﹣∠DME,
又∵∠BHC+∠DME+∠ANF=180°,
∴∠A+∠B+∠C+∠D+∠E+∠F=180°﹣∠ANF+180°﹣∠BHC+180°﹣∠DME,
=540°﹣180°,
=360°.
故答案为:360°.
13.【解答】解:∵AD⊥BC,
∴∠ADC=90°,
∵∠C=70°,
∴∠DAC=180°﹣90°﹣70°=20°,
∵AE平分∠BAC,
∴∠CAE=×50°=25°,
∴∠EAD=∠EAC﹣∠DAC=25°﹣20°=5°.
故答案为:5°.
14.【解答】解:由题意可知,OF=OG,∠FOC=∠DOG,∠FCO=∠GDO=90°,
∴△FCO≌△GDO(AAS),
∴FC=DG,
∵小敏从水平位置CD下降40cm,即DG=40cm,
∴CF=40cm,
又∵点O至地面的距离是50cm,
∴这时小明离地面的高度是50+40=90(cm),
故答案为:90cm.
15.【解答】解:延长PC交BD于E,设AC、PB交于F,
∵∠A+∠ABF+∠AFB=∠P+∠PCF+∠PFC=180°,
∵∠AFB=∠PFC,
∴∠P+∠PCF=∠A+∠ABF,
∵∠P+∠PBE=∠PED,∠PED=∠PCD﹣∠D,
∴∠P+∠PBE=∠PCD﹣∠D,
∴2∠P+∠PCF+∠PBE=∠A﹣∠D+∠ABF+∠PCD,
∵PB、PC是角平分线
∴∠PCF=∠PCD,∠ABF=∠PBE,
∴2∠P=∠A﹣∠D
∵∠A=50°,∠D=10°,
∴∠P=20°.
故答案为:20°.
16.【解答】解:∵CA⊥AB,BM⊥AB,
∠CAB=∠DBE=90°,
∵ED=CB,
当E在线段AB上时,
若BE=AC,
∴Rt△DEB≌Rt△BCA(HL),
∵AE=3t cm,
∴BE=AB﹣AE=(15﹣3t)cm,
∴15﹣3t=6,
∴t=3;
若BE=AB,
∴Rt△DEB≌Rt△CBA(HL),
∴AE=0,
∴t=0(舍去),
当E在线段AB延长线上时,
若BE=AC,
∴Rt△DEB≌Rt△BCA(HL),
∵AE=3t=AB+BE=15+6=21(cm),
∴t=7,
若BE=AB,
∴Rt△DEB≌Rt△CBA(HL),
∵AE=3t=AB+BE=15+15=30(cm),
∴t=10,
∴当t=3或7或10秒时,△DEB与△BCA全等.
故答案为:3或7或10.
三、解答题(本题共8小题,共72分.第17-18题每题6分,第19-20题每题8分,第21-22题每题10分,第23-24题每题12分,解答应写出文字说明、证明过程或演算步骤.)
17.【解答】解:(1)过A点作AM⊥BC于M,
∵AD为BC边上的中线,
∴BD=CD,
∵S△ABD=BD•AM,S△ACD=CD•AM,
∴S△ABD=S△ACD,
故答案为:=;
(2)∵BD=CD,
∴△ABD的周长﹣△ADC的周长=(AB+AD+BD)﹣(AC+AD+CD)=AB﹣AC=4,
即AB﹣AC=4①,
又AB+AC=14②,
①+②得.2AB=18,
解得AB=9,
②﹣①得,2AC=10,
解得AC=5,
∴AB和AC的长分别为:AB=9,AC=5.
18.【解答】解:(1)12边形的内角和为(12﹣2)×180°=1800°,而13边形的内角和为(13﹣2)×180°=1980°,
由于小红说“多边形的内角和不可能是1830°,你一定是多加了一个锐角”,
所以这个“多加的锐角”是1830°﹣1800°=30°,
故答案为:30;
(2)设这个多边形为n边形,由题意得,
(n﹣2)×180°=1800°,
解得n=12,
答:小明求的是12边形内角和;
(3)正十二边形的每一个内角为=150°,
答:这个正多边形的一个内角是150°.
19.【解答】(1)解:由题意得:小刚同学的证明过程中,第一步出现错误;
(2)证明:∵BD=CE,AB=AC,
∴AB﹣BD=AC﹣CE,
∴AD=AE
在△ABE和△ACD中,
,∴△ABE≌△ACD(SAS),
∴∠B=∠C.
20.【解答】(1)证明:∵AB∥DF,
∴∠A=∠EDF,
∵AD=CE,
∴AD+CD=CE+CD,
即AC=DE,
在△ABC和△DFE中,
,
∴△ABC≌△DFE(SAS);
(2)解:∵∠BCF=54°,∠DFC=20°,
∴∠DOC=∠BCF+∠DFC=54°+20°=74°,
∵AB∥DF,
∴∠B=∠DOC=74°,
∵△ABC≌△DFE,
∴∠DFE=∠B=74°.
21.【解答】证明:∵AC⊥BC,DC⊥EC,
∴∠ACB=∠DCE=90°,
∴∠ACE=∠BCD,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(SAS),
∴AE=BD.
22.【解答】解:(1)∵△ABC是“准互余三角形”,∠C>90°,∠A=56°,
∴∠A+2∠B=90°,
∴∠B=17°,
故答案为:17°;
(2)①△ABD是“准互余三角形”,
理由:∵AD是∠BAC的平分线,
∴∠BAC=2∠BAD,
∵∠ACB=90°,
∴∠BAC+∠B=90°,
∴2∠BAD+∠B=90°,
∴△ABD是“准互余三角形”,
②∵△ABE是“准互余三角形”
∴2∠EAB+∠ABC=90°或∠EAB+2∠ABC=90°,
∵∠ABC=28°∴∠EAB=31°或∠EAB=34°,
当∠EAB=31°,∠ABC=28°时,∠AEB=121°,
当∠EAB=34°,∠ABC=28°时,∠AEB=118°,
∴∠AEB的度数为:121°或118°.
23.【解答】(1)证明:∵AE⊥EF,BF⊥EF,
∴∠AEC=∠CFB=90°,
∵∠ACB=90°,
∴∠ACE=90°﹣∠BCF=∠CBF,
在△AEC和△CFB中,
,
∴△AEC≌△CFB(AAS),
∴AE=CF,CE=BF,
∵EF=CF+CE,
∴EF=AE+BF;
(2)解:∵AE⊥EF,BF⊥EF,
∴∠AEC=∠CFB=90°,
∵∠ACB=90°,
∴∠ACE=90°﹣∠BCF=∠CBF,
在△AEC和△CFB中,
,
∴△AEC≌△CFB(AAS),
∴AE=CF,CE=BF,
∵EF=CE﹣CF,
∴EF=BF﹣AE;
故答案为:EF=BF﹣AE;
(3)解:由(2)知AE=CF,
∵EF=4AE,EF=5,
∴AE==CF,
∵EF=BF﹣AE,
∴BF=EF+AE=5+=,
∴△BFC的面积为CF•BF=××=;
故答案为:;
(4)过点A作AE⊥CD于E,过点B作BF⊥CD交DC的延长线于点F,如图:
∵△ADC面积为18且CD的长为9,
∴×9×AE=18,
∴AE=4,
∵∠ADC=45°,AE⊥CD,
∴△ADE是等腰直角三角形,
∴DE=AE=4,
∴CE=CD﹣DE=9﹣4=5,
∵∠ABC=∠CAB=45°,
∴∠ACB=90°,AC=BC,
∴∠ACE=90°﹣∠BCF=∠CBF,
在△ACE和△CBF中,
,
∴△ACE≌△CBF(AAS),
∴BF=CE=5,
∴CD•BF=×9×5=22.5.
故答案为:22.5.
24.【解答】解:(1)在△ABE中,AB=6,BE=AC=10,由三角形三边关系可得:AE﹣AB=4<AE<AB+BE=16,即AE到取值范围为4<AE<16,
∵AD=,
∴AD的取值范围为2<AD<8;
故答案为:2<AD<8;
(2)如图2,延长AE至点F,使得EF=AE,连接DF,则AF=EF+AE=2AE,
∵E是BD中点,
∴DE=BE,
在△EDF和△EBA中,
,
∴△EDF≌△EBA(SAS),
∴DF=AB=CD,∠B=∠EDF,∠F=∠EAB,
∵∠CDA=∠B+∠BAD,∠ADF=∠BDA+∠EDF,∠BDA=∠BAD,
∴∠ADC=∠ADF,
在△AFD和△ACD中,
,
∴△AFD≌△ACD(SAS),
∴AC=AF,
∴AC=2AE;
(3)EF=2AD,EF⊥AD,
理由:如图3,延长DA交EF于点P,延长AD到M,使得DM=AD,连接BM,
由(1)可知,△BDM≌△CDA(SAS),
∴BM=AC,∠M=∠CAD,
∵AC=AF,
∴BM=AF,
由(2)可知,AC∥BM,
∴∠BAC+∠ABM=180°,
∵AE⊥AB、AF⊥AC,
∴∠BAE=∠FAC=90°,
∴∠BAC+∠EAF=180°,
∴∠ABM=∠EAF,
在△ABM和△EAF中,
,
∴△ABM≌△EAF(SAS),
∴AM=EF,∠BAM=∠E,
∵AD=DM,
∴AM=2AD,
∴EF=2AD,
∵∠EAM=∠BAM+∠BAE=∠E+∠APE,
∴∠APE=∠BAE=90°,
∴EF⊥AD.
证明:在△ABE和△ACD中,
…第一步
∴△ABE≌△ACD…第二步
∴∠B=∠C…第三步
山东省日照市东港区新营中学2024-2025学年九年级上学期10月月考数学试卷: 这是一份山东省日照市东港区新营中学2024-2025学年九年级上学期10月月考数学试卷,共5页。
山东省日照市东港区新营中学2024-2025学年七年级上学期10月月考数学试卷: 这是一份山东省日照市东港区新营中学2024-2025学年七年级上学期10月月考数学试卷,共4页。
2023-2024学年山东省日照市东港区新营中学七年级(上)月考数学试卷(10月份)(含解析): 这是一份2023-2024学年山东省日照市东港区新营中学七年级(上)月考数学试卷(10月份)(含解析),共14页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。












