高中数学人教B版 (2019)必修 第三册7.3.3 余弦函数的性质与图修优秀练习题

这是一份高中数学人教B版 (2019)必修 第三册7.3.3 余弦函数的性质与图修优秀练习题，文件包含人教B版2019高中数学必修第三册733余弦函数的性质与图像分层练习原卷docx、人教B版2019高中数学必修第三册733余弦函数的性质与图像分层练习解析卷docx等2份试卷配套教学资源，其中试卷共32页， 欢迎下载使用。

题型一 五点法作余弦函数图像
1． （2023·全国·高一专题练习）用“五点法”作y=2cs2x的图象，首先描出的五个点的横坐标是（ ）
A．0,π2,π,3π2,2πB．0,π4,π2,3π4,π
C．0,π,2π,3π,4πD．0,π6,π3,π2,2π3
【答案】B
【分析】根据五点作图法结合余弦函数的图象即可得解.
【详解】由“五点法”作图知：令2x=0，π2，π，32π，2π，
解得x=0,π4,π2,3π4,π，即为五个关键点的横坐标.
故选：B.
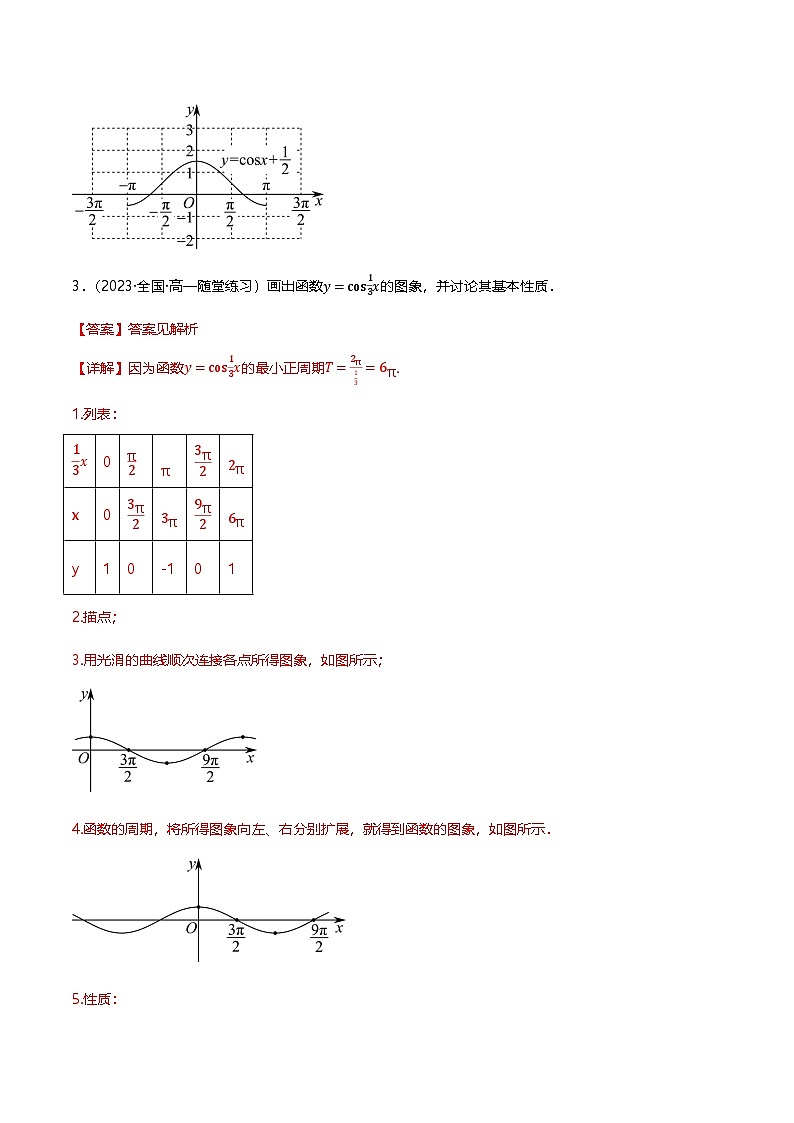
2．（2023上·高一课时练习）用“五点法”作y=csx+12，x∈−π,π的图象.
【答案】图象见解析
【分析】按列表、描点、连线的顺序完成作图.
【详解】（1）取值列表：
（2）描点连线，如图所示.

3．（2023·全国·高一随堂练习）画出函数y=cs13x的图象，并讨论其基本性质．
【答案】答案见解析
【详解】因为函数y=cs13x的最小正周期T=2π13=6π.
1.列表：
2.描点；
3.用光滑的曲线顺次连接各点所得图象，如图所示；

4.函数的周期，将所得图象向左、右分别扩展，就得到函数的图象，如图所示．

5.性质：
定义域：R
值域：[−1,1]
最小正周期：T=6π
单调递增区间：[3π+6kπ,6π+6kπ],k∈Z；
单调递减期间：[6kπ,3π+6kπ],k∈Z.
对称轴：x=3kπ,k∈Z，
对称中心：(3π2+3kπ,0),k∈Z
4．（2023·高一课时练习）作出函数y=csx+π3，x∈−π3,5π3的大致图像．
【答案】见解析
【分析】先根据x的范围，求出x+π3的范围，再根据x+π3找到端点，最大最小值和对称中心，对应的x的值,列表作图.
【详解】∵x∈−π3,5π3∴x+π3∈0,2π
根据五点法作图列表得：
画图像得：
题型二 余弦函数与不等式
1．（2022上·山东德州·高一校考阶段练习）满足csα≥12的角的集合为（ ）
A．αα≥2kπ+π3,k∈ZB．α2kπ−π6≤α≤2kπ+π6,k∈Z
C．α2kπ−π3≤α≤2kπ+π3,k∈ZD．α2kπ+π3≤α≤2kπ+5π3,k∈Z
【答案】C
【分析】利用余弦函数的性质即可求解
【详解】csα≥12结合余弦函数的性质可得2kπ−π3≤α≤2kπ+π3,k∈Z，
故满足csα≥12的角的集合为α2kπ−π3≤α≤2kπ+π3,k∈Z
故选：C
2．（2023·全国·高一随堂练习）求满足csα32，
所以x∈−π6+2kπ,π6+2kπ,k∈Z.
故答案为：−π6+2kπ,π6+2kπ，k∈Z
4. （2023上·高一单元测试）函数y=2cs2x+1的定义域是（ ）
A．{x|2kπ≤x≤2kπ+π2,k∈Z}
B．{x|kπ≤x≤kπ+π2,k∈Z}
C．{x|2kπ≤x≤kπ+π2,k∈Z}
D．{x|kπ−π3≤x≤kπ+π3,k∈Z}
【答案】D
【分析】根据给定的函数有意义，列出不等式，再借助余弦函数的性质求解作答.
【详解】函数y=2cs2x+1有意义，则2cs2x+1≥0，即cs2x≥−12，
因此2kπ−2π3≤2x≤2kπ+2π3,k∈Z，解得kπ−π3≤x≤kπ+π3,k∈Z，
所以函数y=2cs2x+1的定义域是{x|kπ−π3≤x≤kπ+π3,k∈Z}.
故选：D
题型三 与余弦函数有关的零点问题
1．（2021上·高一校考课时练习）直线y=2与函数y=csx的图象的交点个数是（ ）
A．0B．1C．2D．无数个
【答案】A
【分析】利用余弦函数的有界性可得结论.
【详解】因为−1≤csx≤1，故直线y=2与函数y=csx的图象没有公共点，
故选：A.
2．（2023上·高一课时练习）函数y=2sinx的图象与y=csx的图象在0,2π上的交点个数为 .
【答案】2
【分析】作出两个函数在0,2π上的图象，根据图象可得结果.
【详解】作出函数y=2sinx与y=csx在0,2π上的图象，
如图所示：

由图可知，两函数图象在0,2π上有2个交点.
故答案为：2
3. （2021·高一课时练习）方程2x=csx的实根有 .
【答案】无数个
【分析】作出函数y=2x,y=csx的图象，观察两个图象的交点个数即可作答.
【详解】在同一平面直角坐标系中分别画出y=2x与y=csx的图象，如图，
观察图象知，两个函数的图象有无数个交点，即方程2x=csx有无数个实数根.
故答案为：无数个
4．（2022·高一课时练习）函数y=csx，x∈0,2π的图象与直线y=−14的交点有________个．
【答案】2
【分析】再平面直角坐标系下画出函数图象，数形结合即可判断；
【详解】解：
解：作y=csx，x∈0,2π的图象及直线y=−14如下所示，知两函数图象有两个交点．
故答案为：2
题型四 余弦函数的周期性
1．(2024上·黑龙江牡丹江·高一牡丹江市第二高级中学校考期末）函数y=3cs4x+π3的最小正周期是（ ）
A．2πB．π2C．π3D．π
【答案】B
【分析】根据余弦型函数y=Acs(ωx+φ)的最小正周期T=2πω，进而即得.
【详解】由题可知最小正周期T=2π4=π2.
故选：B.
2．（2023·湖南衡阳·高二统考学业考试）函数fx=csx的最小正周期是（ ）
A．πB．2πC．3πD．4π
【答案】B
【分析】根据余弦函数的性质计算可得.
【详解】函数fx=csx的最小正周期T=2π1=2π.
故选：B
3．（2023上·高一课时练习）已知函数 fx=csωx−π6 ω>0 的最小正周期为π6，则ω= .
【答案】12
【分析】根据三角函数的最小正周期公式列方程，解方程求得ω的值.
【详解】由于ω>0，依题意可知T=2πω=2πω=π6⇒ω=12.
故答案为：12
4．（2023下·上海静安·高一校考期中）函数y=csx3的最小正周期是 ．
【答案】6π
【分析】根据余弦函数的最小正周期公式，即可求得答案.
【详解】函数y=csx3的最小正周期是T=2π13=6π，
故答案为：6π
题型五 余弦函数的奇偶性
1．（2023上·山西·高二统考学业考试）函数y=cs2x是（ ）
A．周期为π的偶函数B．周期为π的奇函数C．周期为π2的偶函数D．周期为π2的奇函数
【答案】A
【分析】计算周期和奇偶性得到答案.
【详解】y=fx=cs2x，函数定义域为R，T=2π2=π，f−x=cs−2x=cs2x=fx，
y=fx=cs2x为偶函数，
故选：A
2．（2023下·新疆和田·高一校考阶段练习）函数y=sin(5π2−2x)是（ ）
A．奇函数B．偶函数C．非奇非偶函数D．以上都不对
【答案】B
【分析】利用诱导公式化简给定的函数，再利用余弦函数性质判断作答.
【详解】依题意，函数y=sin(5π2−2x)，化为y=cs2x是偶函数.
故选：B
3．（2022下·上海杨浦·高一上海市控江中学校考期中）函数f(x)=sin3π2+x的奇偶性为 函数.（填“奇”、“偶”或“非奇非偶”）
【答案】偶函数
【分析】先根据诱导公式对函数进行化简，最后利用余弦函数的奇偶性判断即可.
【详解】由已知条件得f(x)=sin3π2+x=−csx，且函数定义域为R，关于原点对称，
则f−x=−cs−x=−csx=fx，
故函数为偶函数；
故答案为：偶函数.
4．（2023·全国·高一随堂练习）下列函数哪些是奇函数？哪些是偶函数？哪些既不是奇函数也不是偶函数？
(1)y=1−sinx；
(2)y=−3sinx；
(3)y=1−csx；
(4)y=csx．
【答案】(1)既不是奇函数，又不是偶函数
(2)奇函数
(3)偶函数
(4)偶函数
【分析】先看定义域是否关于原点对称，再利用奇函数和偶函数的定义进行判断.
【详解】（1）fx=1−sinx定义域为R，
又f−x=1−sin−x=1+sinx≠fx，且f−x=1+sinx≠−fx，
故fx=1−sinx既不是奇函数，又不是偶函数；
（2）gx=−3sinx的定义域为R，
又g−x=−3sin−x=3sinx=−gx，故gx=−3sinx为奇函数；
（3）ℎx=1−csx定义域为R，
且ℎ−x=1−cs−x=1−csx=ℎx，故ℎx=1−csx为偶函数；
（4）kx=csx定义域为R，
且k−x=cs−x=csx=kx，故kx=csx为偶函数.
题型六 余弦函数的对称轴与对称中心问题
1．（2023下·重庆·高一校联考阶段练习）函数fx=csx−π7图象的对称轴方程是（ ）
A．x=9π14+kπk∈ZB．x=9π14+2kπk∈Z
C．x=π7+kπk∈ZD．x=π7+2kπk∈Z
【答案】C
【分析】采用整体对应法即可构造方程求得对称轴方程.
【详解】令x−π7=kπk∈Z，解得：x=π7+kπk∈Z，
∴fx的对称轴方程为x=π7+kπk∈Z.
故选：C.
2．（2023下·湖北黄冈·高一校考阶段练习）函数y=32csx+π2的图象的一条对称轴方程是（ ）
A．x=−π2B．x=−π4C．x=π8D．x=π
【答案】A
【分析】利用整体思想直接代入余弦函数对称轴的性质即可求解.
【详解】依题意，
由x+π2=kπ，k∈Z，得x=−π2+kπ，k∈Z．
当k=0时，得x=−π2.
故选：A.
3．（2020上·高一课时练习）函数y=3cs2x−π8的一个对称中心是（ ）
A．π8,0B．5π16,0C．3π8,0D．7π16,0
【答案】B
【分析】计算余弦型函数的对称中心，然后直接进行判断即可.
【详解】令2x−π8=π2+kπ,k∈Z，则x=5π16+kπ2,k∈Z
所以函数y=3cs2x−π8的对称中心为5π16+kπ2,0,k∈Z
令k=0，所以函数y=3cs2x−π8的一个对称中心是5π16,0
故选：B
【点睛】本题考查余弦型函数的对称中心，属基础题.
4．（2023上·北京·高一北京市十一学校校考期末）函数y=4cs2x+π3的对称中心为 .
【答案】kπ2+π12,0，k∈Z.
【分析】利用整体代换法求解对称中心.
【详解】令2x+π3=kπ+π2,k∈Z，
解得x=kπ2+π12,k∈Z
故函数y=4cs2x+π3的对称中心为kπ2+π12,0，k∈Z.
故答案为：kπ2+π12,0，k∈Z.
题型七 根据奇偶性对称性求参数
1．（2023·江西景德镇·统考模拟预测）将函数fx=cs2x+φ的图像向右移π6后关于原点中心对称，则φ可能的取值是（ ）
A．−π3B．−π6C．π6D．π3
【答案】B
【分析】先利用平移变换，得到gx=cs2x+φ−π3，再根据gx的图象关于原点中心对称，由φ−π3=kπ+π2,k∈Z求解.
【详解】解：将函数fx=cs2x+φ的图像向右移π6得到gx=cs2x+φ−π3，
因为gx的图象关于原点中心对称，
所以φ−π3=kπ+π2,k∈Z，即φ=kπ+5π6,k∈Z，
所以φ可能的取值是−π6，
故选：B
2．（2022上·黑龙江哈尔滨·高一哈师大附中校考阶段练习）设函数fx=2cs2x+φ的图象关于点5π6,0中心对称，则φ的最小值为（ ）
A．7π6B．5π6C．π3D．π6
【答案】D
【分析】利用5π6,0为对称中心，列出方程，求出φ=−7π6+kπ，k∈Z，求出φ的最小值.
【详解】由题意得：2×5π6+φ=π2+kπ，k∈Z，
解得：φ=−7π6+kπ，k∈Z，
所以φ=−7π6+kπ，k∈Z，
当k=1时，φ取得最小值为π6.
故选：D
3．（2022·北京·人大附中校考模拟预测）函数fx=csωx−π3(ω>0)的图像关于直线x=π2对称，则ω可以为（ ）
A．13B．12C．23D．1
【答案】C
【分析】f(x)=cs(ωx−π3)(ω>0)的对称轴为ωx−π3=kπ，化简得到ω=2k+23(ω>0)得到答案.
【详解】f(x)=cs(ωx−π3)(ω>0)
对称轴为：ωx−π3=kπ⇒π2ω−π3=kπ⇒ω=2k+23(ω>0)(k∈Z)
当k=0时，ω取值为23.
故选:C.
4．（2023下·内蒙古呼和浩特·高一呼和浩特市土默特中学校考期中）若函数fx=cs2x+φ−π≤φaB．c>b>aC．c>a>bD．b>a>c
【答案】B
【分析】利用诱导公式，可将b，c变形为cs44°，cs43°，根据余弦函数的单调性，即可求得答案.
【详解】由题意得： b=sin(180°−46°)=sin46°=sin(90°−44°)=cs44°，c=cs43°，
因为y=csx在(0,90°)上单调递减，
所以cs43°>cs44°>cs46°，即c>b>a．
故选：B
2．（2020上·江西鹰潭·高一贵溪市实验中学校考阶段练习）三个数cs−π8，csπ5，cs3π5的大小关系（ ）
A．cs−π8