天津市第七中学2024-2025学年 八年级上学期第一次月考数学试卷

这是一份天津市第七中学2024-2025学年 八年级上学期第一次月考数学试卷，共12页。试卷主要包含了有下列说法，其中正确的有等内容，欢迎下载使用。
1．如图，窗户打开后，用窗钩AB可将其固定，其所运用的几何原理是（ ）
A．两点之间，线段最短B．两点确定一条直线
C．垂线段最短D．三角形具有稳定性
2．有下列说法，其中正确的有（ ）
①两个等边三角形一定能完全重合；
②如果两个图形是全等图形，那么它们的形状和大小一定相同；
③两个等腰三角形一定是全等图形；
④面积相等的两个图形一定是全等图形．
A．1个B．2个C．3个D．4个
3．如图，在△ABC中，BC边上的高为（ ）
A．BFB．CFC．BDD．AE
4．三角形的三边长分别为5，8，x，则最长边x的取值范围是（ ）
A．3＜x＜8B．5＜x＜13C．3＜x＜13D．8≤x＜13
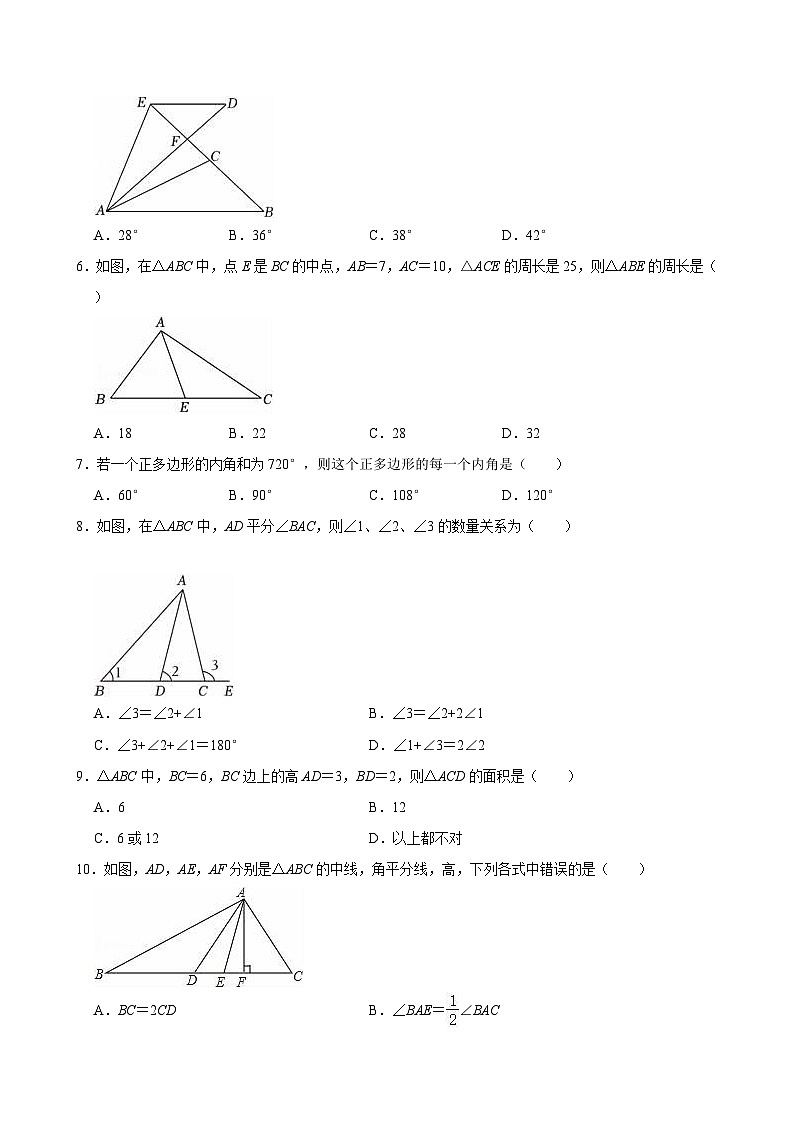
5．如图，△ABC≌△ADE，线段BC的延长线过点E，与线段AD交于点F，∠AED＝108°，∠CAD＝12°，∠B＝48°，则∠DEF的度数为（ ）
A．28°B．36°C．38°D．42°
6．如图，在△ABC中，点E是BC的中点，AB＝7，AC＝10，△ACE的周长是25，则△ABE的周长是（ ）
A．18B．22C．28D．32
7．若一个正多边形的内角和为720°，则这个正多边形的每一个内角是（ ）
A．60°B．90°C．108°D．120°
8．如图，在△ABC中，AD平分∠BAC，则∠1、∠2、∠3的数量关系为（ ）
A．∠3＝∠2+∠1B．∠3＝∠2+2∠1
C．∠3+∠2+∠1＝180°D．∠1+∠3＝2∠2
9．△ABC中，BC＝6，BC边上的高AD＝3，BD＝2，则△ACD的面积是（ ）
A．6B．12
C．6或12D．以上都不对
10．如图，AD，AE，AF分别是△ABC的中线，角平分线，高，下列各式中错误的是（ ）
A．BC＝2CDB．∠BAE＝∠BAC
C．∠AFB＝90°D．AE＝CE
11．如图所示，△ABC中，点D、E、F分别在三边上，E是AC的中点，AD、BE、CF交于一点G，BD＝2DC，S△GEC＝3，S△GDC＝4，则△ABC的面积是（ ）
A．25B．30C．35D．40
12．如图，△ABC的两条内角平分线BO，CO相交于点O，两条外角平分线BP，CP相交于点P．已知∠BOC＝120°，则∠P＝（ ）
A．60°B．50°C．40°D．30°
二．填空题（共6小题）
13．若一个多边形的每个外角都等于30°，则这个多边形的边数为 ．
14．如图，∠1＝20°，∠2＝30°，∠BDC＝95°，则∠A的度数是 ．
15．如果一个正方形被截掉一个角后，得到一个多边形，那么这个多边形的内角和是 ．
16．若一个多边形截去一个角后，形成的另一个多边形的内角和是1620°，则原来的多边形的边数是 ．
17．如图，△ABC的顶点分别为A（0，3），B（﹣4，0），C（2，0），且△BCD与△ABC全等，则点D坐标可以是 ．
18．如图，在△ABC中，∠ACB＝90°，AB＝5，BC＝3，AC＝4，P是AB边上的动点（不与点B重合），将△BCP沿CP所在的直线翻折，得到△B′CP，连接B′A，则B′A长度的最小值是 ．
三．解答题（共5小题）
19．如图，在△ABC中，∠B＝∠C，点D，E在边BC上，AD＝AE．
（1）求证：△ABD≌△AEC；
（2）若∠ADE＝60°，AD＝6，BE＝8，求BD的长度．
20．如图，AD为△ABC的角平分线，DE∥AB交AC于点E，若∠BAC＝58°，∠C＝65°，求∠ADE和∠EDC的度数．
21．如图，已知△ABC和△ADE，AB＝AD，∠BAD＝∠CAE，∠B＝∠D，AD与BC交于点P，点C在DE上．求证：BC＝DE．
22．如图，在△ABC中，AD⊥BC，AE平分∠BAC，∠B＝70°，∠C＝30°，求：
（1）∠BAE的度数；
（2）∠DAE的度数．
23．探究与发现：如图①，在△ABC中，∠B＝∠C＝45°，点D在BC边上，点E在AC边上，且∠ADE＝∠AED，连接DE．
（1）当∠BAD＝60°时，求∠CDE的度数；
（2）当点D在BC（点B、C除外）边上运动时，试探究∠BAD与∠CDE的数量关系；
（3）深入探究：如图②，若∠B＝∠C，但∠C≠45°，其它条件不变，试继续探究∠BAD与∠CDE的数量关系．
2024-2025学年天津七中八年级（上）第一次月考数学试卷
参考答案与试题解析
一．选择题（共12小题）
1．【解答】解：一扇窗户打开后，用窗钩将其固定，正好形成三角形的形状，
所以，主要运用的几何原理是三角形的稳定性．
故选：D．
2．【解答】解：①两个等边三角形不一定能完全重合，故此选项不合题意；
②如果两个图形是全等图形，那么它们的形状和大小一定相同，故此选项符合题意；
③两个等腰三角形不一定是全等图形，故此选项不合题意；
④面积相等的两个图形不一定是全等图形，故此选项不合题意．
故选：A．
3．【解答】解：根据高的定义，AE为△ABC中BC边上的高．
故选：D．
4．【解答】解：∵5+8＝13，8﹣5＝3，
∴3＜x＜13，
又∵x是三角形中最长的边，
∴8≤x＜13．
故选：D．
5．【解答】解：∵∠ACB＝108°，∠B＝48°，
∴∠CAB＝180°﹣∠B﹣∠ACB＝180°﹣48°﹣108°＝24°．
又∵△ABC≌△ADE，
∴∠EAD＝∠CAB＝24°．
又∵∠EAB＝∠EAD+∠CAD+∠CAB，∠CAD＝12°，
∴∠EAB＝24°+12°+24°＝60°，
∴∠AEB＝180°﹣∠EAB﹣∠B＝180°﹣60°﹣48°＝72°，
∴∠DEF＝∠AED﹣∠AEB＝108°﹣72°＝36°．
故选：B．
6．【解答】解：∵点E是BC的中点，
∴BE＝CE，
∵AB＝7，AC＝10，
∴△ACE的周长＝AC+CE+AE＝25＝10+CE+AE，
∴CE+AE＝15，
∴△ABE的周长＝AB+BE+AE＝7+CE+AE＝7+15＝22，
故选：B．
7．【解答】解：（n﹣2）×180°＝720°，
∴n﹣2＝4，
∴n＝6．
则这个正多边形的每一个内角为720°÷6＝120°．
故选：D．
8．【解答】解：∵AD平分∠BAC，
∴∠DAC＝∠BAD，
∴∠3＝∠2+∠DAC＝∠2+∠BAD，
∵∠1+∠BAD＝∠2，
∴∠1+∠3＝∠1+∠2+∠BAD＝2∠2．
故选：D．
9．【解答】解：当AD在△ABC内部时，
∵BC＝6，BD＝2，
∴CD＝BC﹣BD＝4，
又BC边上的高AD＝3，
∴△ACD的面积是；
当AD在△ABC外部时，
∵BC＝6，BD＝2，
∴CD＝BC+BD＝8，
又BC边上的高AD＝3，
∴△ACD的面积是；
综上，△ACD的面积是6或12．
故选：C．
10．【解答】解：∵AD，AE，AF分别是△ABC的中线，角平分线，高，
∴BC＝2BD＝2DC，∠BAE＝∠CAE＝∠BAC，∠AFB＝∠AFC＝90°，
故选项A、B、C正确，选项D错误，
故选：D．
11．【解答】解：BD＝2DC，
∴S△ABD＝2S△ACD，
∴S△ABC＝3S△ACD，
∵E是AC的中点，
∴S△AGE＝S△CGE，
又∵S△GEC＝3，S△GDC＝4，
∴S△ACD＝S△AGE+S△CGE+S△CGD＝3+3+4＝10，
∴S△ABC＝3S△ACD＝3×10＝30．
故选：B．
12．【解答】解：∵∠BOC＝120°，
∴∠OBC+∠OCB＝180°﹣∠BOC＝180°﹣120°＝60°，
又∵BO，CO是∠ABC，∠ACB的角平分线，
∴∠ABC+∠ACB＝2（∠OBC+∠OCB）＝2×60°＝120°，
∴∠CBD+∠BCE＝360°﹣（∠ABC+∠ACB）＝360°﹣120°＝240°，
∵BP，CP是∠CBD，∠BCE的角平分线，
∴，
∴∠P＝180﹣（∠CBP+∠BCP）＝60°，
故选：A．
二．填空题（共6小题）
13．【解答】解：∵一个多边形的每个外角都等于30°，
又∵多边形的外角和等于360°，
∴多边形的边数是＝12，
故答案为：12．
14．【解答】解：∵∠BDC＝95°，
∴∠DBC+∠DCB＝180°﹣95°＝85°，
∵∠1＝20°，∠2＝30°，
∴∠ABC+∠ACB＝85°+20°+30°＝135，
在△ABC中，∠A＝180°﹣（∠ABC+∠ACB）＝180°﹣135°＝45°．
故答案为：45°．
15．【解答】解：n边形的内角和是（n﹣2）•180°，
边数增加1，则新的多边形的内角和是（4+1﹣2）×180°＝540°，
所得新的多边形的边数不变，则新的多边形的内角和是（4﹣2）×180°＝360°，
所得新的多边形的边数减少1，则新的多边形的内角和是（4﹣1﹣2）×180°＝180°，
因而所成的新多边形的内角和是540°或360°或180°．
故答案为：540°或360°或180°．
16．【解答】解：多边形的内角和可以表示成（n﹣2）•180°（n≥3且n是整数），一个多边形截去一个角后，多边形的边数可能增加了一条，也可能不变或减少了一条，
根据（n﹣2）•180°＝1620°，
解得：n＝11，
则多边形的边数是10，11或12．
故答案为10，11或12．
17．【解答】解：如图所示，△BCD与△ABC全等，点D可以和点A重合，故点D坐标可以是（﹣2，3）或（﹣2，﹣3）或（0，﹣3）或（0，3）．
故答案为：（﹣2，3）或（﹣2，﹣3）或（0，﹣3）或（0，3）．
18．【解答】解：由翻转变换的性质可知：BC＝CB′＝3，
∵CB′长度固定不变，
∴当AB′+CB′有最小值时，AB′的长度有最小值．
根据两点之间线段最短可知：A、B′、C三点在一条直线上时，AB′有最小值，
∴AB′＝AC﹣B′C＝4﹣3＝1．
故答案为：1．
三．解答题（共5小题）
19．【解答】（1）证明：∵AD＝AE，
∴∠ADE＝∠AED，
∴∠ADB＝∠AEC，
∵∠B＝∠C，AD＝AE，
∴△ABD≌△AEC（AAS）；
（2）解：∵∠ADE＝60°，AD＝AE，
∴△ADE为等边三角形，
∴AD＝DE＝6，
∴BD＝BE﹣DE＝8﹣6＝2．
20．【解答】解：∵在△ABC中，∠BAC＝58°，∠C＝65°，
∴∠ABC＝180°﹣∠BAC﹣∠C＝57°，
∵AD是△ABC的角平分线，
∴∠BAD＝∠BAC＝29°，
∵DE∥AB，
∴∠ADE＝∠BAD＝29°，∠EDC＝∠ABC＝57°．
21．【解答】证明：∵∠BAD＝∠CAE，
∴∠BAD+∠DAC＝∠CAE+∠DAC，
即∠BAC＝∠DAE，
在△ABC和△ADE中，
，
∴△ABC≌△ADE（ASA），
∴BC＝DE．
22．【解答】解：（1）∵∠B+∠C+∠BAC＝180°，
∴∠BAC＝180°﹣∠B﹣∠C
＝180°﹣70°﹣30°
＝80°．
∵AE平分∠BAC，
∴．
（2）∵AD⊥BC，
∴∠ADB＝90°，
∴∠BAD＝90°﹣∠B
＝90°﹣70°
＝20°．
∴∠DAE＝∠BAE﹣∠BAD
＝40°﹣20°
＝20°．
23．【解答】解：（1）∵∠ADC是△ABD的外角，
∴∠ADC＝∠B+∠BAD＝105°，
∵∠AED是△CDE的外角，
∴∠AED＝∠C+∠EDC，
∵∠B＝∠C，∠ADE＝∠AED，
∴∠ADC﹣∠EDC＝105°﹣∠EDC＝45°+∠EDC，
解得：∠EDC＝30°．
（2）∠EDC＝∠BAD．
证明：设∠BAD＝x，
∵∠ADC是△ABD的外角，
∴∠ADC＝∠B+∠BAD＝45°+x，
∵∠AED是△CDE的外角，
∴∠AED＝∠C+∠EDC，
∵∠B＝∠C，∠ADE＝∠AED，
∴∠ADC﹣∠EDC＝45°+x﹣∠EDC＝45°+∠EDC，
解得：∠EDC＝∠BAD．
（3）∠EDC＝∠BAD．
证明：设∠BAD＝x，
∵∠ADC是△ABD的外角，
∴∠ADC＝∠B+∠BAD＝∠B+x，
∵∠AED是△CDE的外角，
∴∠AED＝∠C+∠EDC，
∵∠B＝∠C，∠ADE＝∠AED，
∴∠ADC﹣∠EDC＝∠B+x﹣∠EDC＝∠B+∠EDC，
解得：∠EDC＝∠BAD．