石嘴山市重点中学2024年九上数学开学预测试题【含答案】

这是一份石嘴山市重点中学2024年九上数学开学预测试题【含答案】，共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）如图，矩形中，，，、分别是边、上的点，且与之间的距离为4，则的长为（ ）
A．3B．C．D．
2、（4分）下列数据中不能作为直角三角形的三边长的是（ ）
A．1、B．C．5、12、13D．1、2、3
3、（4分）下列因式分解正确的是（ ）
A．2x2﹣2＝2（x+1）（x﹣1）B．x2+2x﹣1＝（x﹣1）2
C．x2﹣1＝（x﹣1）2D．x2﹣x+2＝x（x﹣1）+2
4、（4分）对于函数 y＝3-x，下列结论正确的是（ ）
A．y 的值随 x 的增大而增大B．它的图象必经过点（-1,3）
C．它的图象不经过第三象限D．当 x＞1 时，y＜0.
5、（4分）下面哪个点在函数y＝2x－1的图象上（ ）
A．(－2.5，－4)B．(1，3)C．(2.5，4)D．(0，1)
6、（4分）若，则= ( )
A．B．C．D．无法确定
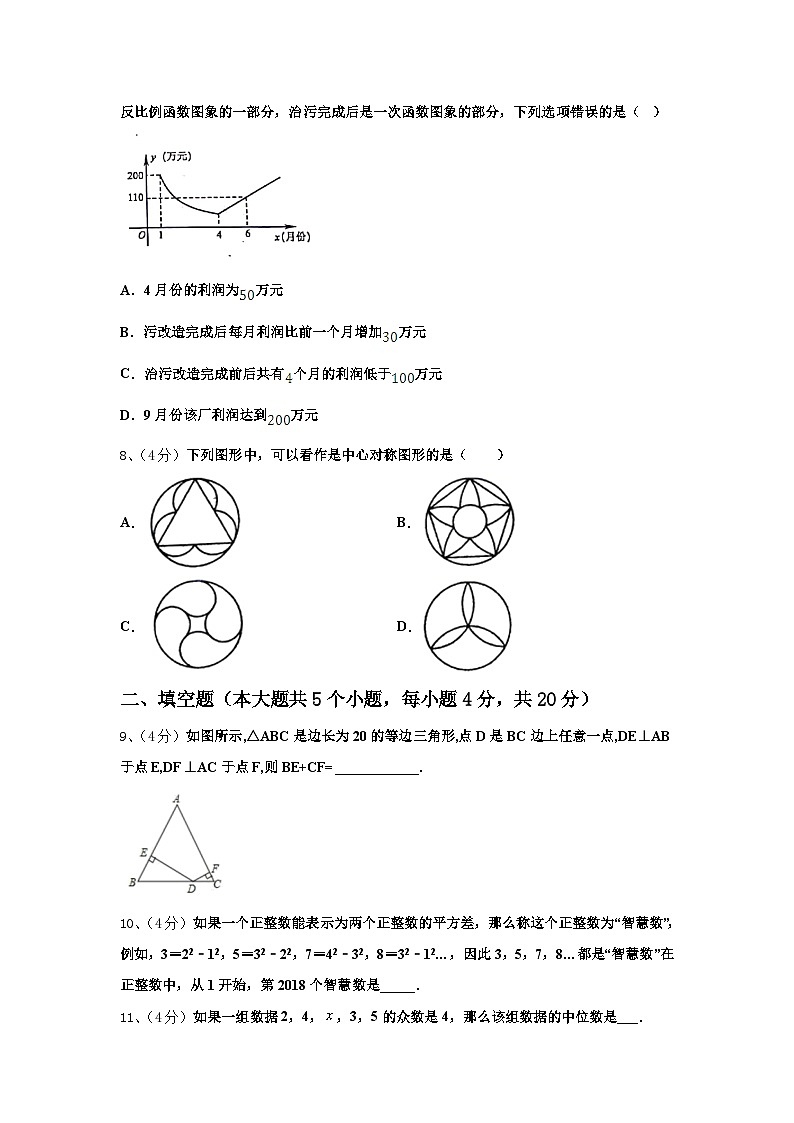
7、（4分）为了响应“绿水青山就是金山银山”的号召，建设生态文明，某工厂自2019年1月开始限产并进行治污改造，其月利润(万元)与月份之间的变化如图所示，治污完成前是反比例函数图象的一部分，治污完成后是一次函数图象的部分，下列选项错误的是（ ）
A．4月份的利润为万元
B．污改造完成后每月利润比前一个月增加万元
C．治污改造完成前后共有个月的利润低于万元
D．9月份该厂利润达到万元
8、（4分）下列图形中，可以看作是中心对称图形的是（ ）
A．B．
C．D．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图所示,△ABC是边长为20的等边三角形,点D是BC边上任意一点,DE⊥AB于点E,DF⊥AC于点F,则BE+CF=____________.
10、（4分）如果一个正整数能表示为两个正整数的平方差，那么称这个正整数为“智慧数”，例如，3＝22﹣12，5＝32﹣22，7＝42﹣32，8＝32﹣12…，因此3，5，7，8…都是“智慧数”在正整数中，从1开始，第2018个智慧数是_____．
11、（4分）如果一组数据2，4，，3，5的众数是4，那么该组数据的中位数是___．
12、（4分）一个矩形的长比宽多1cm，面积是132cm2，则矩形的长为________cm．
13、（4分）如图，在四边形ABCD中，P是对角线BD的中点，E、F分别是AB、CD的中点，AD=BC，∠EPF=147°，则∠PFE的度数是___．
三、解答题（本大题共5个小题，共48分）
14、（12分）因式分解：2
15、（8分）解不等式组并求其整数解的和.
解：解不等式①，得_______；
解不等式②，得________；
把不等式①和②的解集在数轴上表示出来：
原不等式组的解集为________，
由数轴知其整数解为________，和为________.
在解答此题的过程中我们借助于数轴上，很直观地找出了原不等式组的解集及其整数解，这就是“数形结合的思想”，同学们要善于用数形结合的思想去解决问题.
16、（8分）八年级全体同学参加了学校捐款活动，随机抽取了部分同学捐款的情况统计图如图所示
（1）本次共抽查学生 人，并将条形统计图补充完整；
（2）捐款金额的众数是 ，中位数是 ；
（3）在八年级600名学生中，捐款20元及以上的学生估计有 人.
17、（10分）如图，的对角线相交于点，直线EF过点O分别交BC，AD于点E、F，G、H分别为OB、OD的中点，求证：四边形GEHF是平行四边形．
18、（10分）如图，直线y=kx+b经过点A（-5，0），B（-1，4）
（1）求直线AB的表达式；
（2）求直线CE：y=-2x-4与直线AB及y轴围成图形的面积；
（3）根据图象，直接写出关于x的不等式kx+b＞-2x-4的解集．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）若关于x的一元二次方程有实数根，且所有实数根均为整数，请写出一个符合条件的常数m的值:m=_____.
20、（4分）如图，□ABCD的对角线AC，BD相交于点O，若AO+BO=5，则AC+BD的长是________．
21、（4分）正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图所示的方式放置．点A1，A2，A3，…和点C1，C2，C3，…分别在直线y=kx+b（k＞0）和x轴上，已知点B1（1，1），B2（3，2），则B5的坐标是_____________ 。
22、（4分）菱形的边长为5，一条对角线长为8，则菱形的面积为____．
23、（4分）如图，在平面直角坐标系中，矩形纸片OABC的顶点A，C分别在x轴，y轴的正半轴上，将纸片沿过点C的直线翻折，使点B恰好落在x轴上的点B′处，折痕交AB于点D．若OC=9，，则折痕CD所在直线的解析式为____．
二、解答题（本大题共3个小题，共30分）
24、（8分）解方程
(1)
(2)
(3)
(4) (公式法)
25、（10分）如图，正方形ABCD中，AC是对角线，今有较大的直角三角板，一边始终经过点B，直角顶点P在射线AC上移动，另一边交DC于Q．
（1）如图①，当点Q在DC边上时，猜想并写出PB与PQ所满足的数量关系，并加以证明；
（2）如图②，当点Q落在DC的延长线上时，猜想并写出PB与PQ满足的数量关系，并证明你的猜想．
26、（12分）如图，在平面直角标系中，△ABC的三个顶点坐标为A（-3，1）、B（-4，-3）、C（-1，-4），△ABC绕原点顺时针旋转180°，得到△A1B1C1再将△A1B1C1向左平移5个单位得到△A1B1C1．
（1）画出△A1B1C1，并写出点A的对应点A1的坐标；
（1）画出△A1B1C1，并写出点A的对应点A1的坐标；
（3）P（a，b）是△ABC的边AC上一点，△ABC经旋转，平移后点P的对应点分别为P1、P1，请直接写出点P1的坐标．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、D
【解析】
过点D作DG⊥BE，垂足为G，则GD＝4＝AB，∠G＝90°，再利用AAS证明△AEB≌△GED，根据全等三角形的性质可得AE＝EG． 设AE＝EG＝x，则ED＝5﹣x，在Rt△DEG中，由勾股定理得可得方程x2+42＝（5﹣x）2， 解方程求得x的值即可得AE的长．
【详解】
过点D作DG⊥BE，垂足为G，如图所示：

则GD＝4＝AB，∠G＝90°，
∵四边形ABCD是矩形，
∴AD＝BC＝5，∠A＝90°＝∠G，
在△AEB和△GED中，
∴△AEB≌△GED（AAS）．
∴AE＝EG．
设AE＝EG＝x，则ED＝5﹣x，
在Rt△DEG中，由勾股定理得：ED2＝EG2+GD2，
∴x2+42＝（5﹣x）2，
解得：x＝，即AE＝．
故选D．
本题考查了矩形的性质、全等三角形的判定与性质及勾股定理，正确作出辅助线，证明AE＝EG是解决问题的关键.
2、D
【解析】
根据勾股定理的逆定理进行计算分析，从而得到答案．
【详解】
A、12+（）2＝（）2，能构成直角三角形，故选项错误；
B、（）2+（）2＝（）2，能构成直角三角形，故选项错误；
C、52+122＝132，能构成直角三角形，故选项错误；
D、12+22≠32，不能构成直角三角形，故选项正确，
故选D．
本题考查了勾股定理的逆定理：已知三角形ABC的三边满足a2+b2＝c2，则三角形ABC是直角三角形．
3、A
【解析】
由题意根据因式分解的意义，即可得答案判断选项．
【详解】
解：A、2x2﹣2＝2（x2﹣1）＝2（x+1）（x﹣1），故A符合题意；
B、x2+2x+1＝（x+1）2，故B不符合题意；
C、x2﹣1＝（x+1）（x﹣1），故C不符合题意；
D、不能分解，故D不符合题意；
故选：A．
本题考查因式分解的意义，一提，二套，三检查，注意分解要彻底．
4、C
【解析】
根据函数的增减性判断A；
将（-1,3）的横坐标代入函数解析式，求得y，即可判断B；
根据函数图像与系数的关系判断C；
根据函数图像与x轴的交点可判断D.
【详解】
函数y＝3-x，k=-1＜0，b=3＞0，
所以函数经过一、二、四象限，y随x的增大而减小，
故A错误，C正确；
当x=-1时，y=4，所以图像不经过（-1,3），故B错误；
当y=0时，x=3，又因为y随x的增大而减小，
所以当x＞3时，y＜0，故D错误.
故答案为C.
本题考查一次函数的图像与性质，熟练掌握图像与系数的关系，数形结合是解决函数类问题的关键.
5、C
【解析】
将点的坐标逐个代入函数解析式中，若等号两边相等则点在函数上，否则就不在．
【详解】
解：将x=-2.5，y=-4代入函数解析式中，等号左边-4，等号右边-6，故选项A错误；
将x=1，y=3代入函数解析式中，等号左边3，等号右边1，故选项B错误；
将x=2.5，y=4代入函数解析式中，等号左边4，等号右边4，故选项C正确；
将x=0，y=1代入函数解析式中，等号左边1，等号右边-1，故选项D错误；
故选：C．
本题考查了一次函数图像上点的坐标特征，一次函数y=kx+b，（k≠0，且k，b为常数）的图像是一条直线．直线上任意一点的坐标都满足函数关系式y=kx+b．
6、B
【解析】
设比值为，然后用表示出、、，再代入算式进行计算即可求解.
【详解】
设，
则，，，
.
故选：.
本题考查了比例的性质，利用设“”法表示出、、是解题的关键，设“”法是中学阶段常用的方法之一，需熟练掌握并灵活运用.
7、C
【解析】
首先设反比例函数和一次函数的解析式，根据图像信息，即可得出解析式，然后即可判断正误.
【详解】
设反比例函数解析式为
根据题意，图像过点（1,200），则可得出
当时，，即4月份的利润为万元，A选项正确；
设一次函数解析式为
根据题意，图像过点（4,50）和（6,110）
则有
解得
∴一次函数解析式为，其斜率为30，即污改造完成后每月利润比前一个月增加万元，B选项正确；
治污改造完成前后，1-6月份的利润分别为200万元、100万元、万元、50万元、110万元，共有3个月的利润低于万元，C选项错误；
9月份的利润为万元，D选项正确；
故答案为C.
此题主要考查一次函数和反比例函数的实际应用，熟练掌握，即可解题.
8、C
【解析】
根据中心对称的定义，结合所给图形即可作出判断．
【详解】
解：A、不是中心对称图形，故本选项不合题意；
B、不是中心对称图形，故本选项不合题意；
C、是中心对称图形，故本选项符合题意；
D、不是中心对称图形，故本选项不合题意；
故选：C．
本题考查了中心对称图形的特点，属于基础题，判断中心对称图形的关键是旋转180°后能够重合．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、10
【解析】
先设BD=x，则CD=20-x，根据△ABC是等边三角形，得出∠B=∠C=60°，再利用三角函数求出BE和CF的长，即可得出BE+CF的值．
【详解】
设BD=x，则CD=20−x，
∵△ABC是等边三角形，
∴∠B=∠C=60∘.
∴BE=cs60∘⋅BD=，
同理可得,CF=，
∴BE+CF=+=10.
本题考查等边三角形的性质，解题的关键是掌握等边三角形的性质.
10、1693
【解析】
如果一个数是智慧数，就能表示为两个正整数的平方差，设这两个数分别m、n，设m＞n，即智慧数=m1-n1=（m+n）（m-n），因为m，n是正整数，因而m+n和m-n就是两个自然数．要判断一个数是否是智慧数，可以把这个数分解因数，分解成两个整数的积，看这两个数能否写成两个正整数的和与差．
【详解】
解：1不能表示为两个正整数的平方差，所以1不是“智慧数”．对于大于1的奇正整数1k+1，有1k+1=（k+1）1-k1（k=1，1，…）．所以大于1的奇正整数都是“智慧数”．
对于被4整除的偶数4k，有4k=（k+1）1-（k-1）1（k=1，3，…）．
即大于4的被4整除的数都是“智慧数”，而4不能表示为两个正整数平方差，所以4不是“智慧数”．
对于被4除余1的数4k+1（k=0，1，1，3，…），设4k+1=x1-y1=（x+y）（x-y），其中x，y为正整数，
当x，y奇偶性相同时，（x+y）（x-y）被4整除，而4k+1不被4整除；
当x，y奇偶性相异时，（x+y）（x-y）为奇数，而4k+1为偶数，总得矛盾．
所以不存在自然数x，y使得x1-y1=4k+1．即形如4k+1的数均不为“智慧数”．
因此，在正整数列中前四个正整数只有3为“智慧数”，此后，每连续四个数中有三个“智慧数”．
因为1017=（1+3×671），4×（671+1）=1691，
所以1693是第1018个“智慧数”，
故答案为：1693．
本题考查平方差公式，有一定的难度，主要是对题中新定义的理解与把握．
11、1
【解析】
根据众数为1，可得x等于1，然后根据中位数的概念，求解即可．
【详解】
解：因为这组数据的众数是1，
∴x=1，
则数据为2、3、1、1、5，
所至这组数据的中位数为1，
故答案为：1．
本题考查了众数和中位数的概念：一组数据中出现次数最多的数据叫做众数；将一组数据按照从小到大（或从大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数；如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数．
12、1
【解析】
设矩形的宽为xcm，根据矩形的面积=长×宽列出方程解答即可．
【详解】
设矩形的宽为xcm，依题意得：
x（x+1）=132，
整理，得（x+1）（x-11）=0，
解得x1=-1（舍去），x2=11，
则x+1=1．
即矩形的长是1cm．
故答案为：1．
本题考查了一元二次方程的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程，再求解．
13、16.5°
【解析】
根据三角形中位线定理得到PE=AD，PF=BC，根据等腰三角形的性质、三角形内角和定理计算即可．
【详解】
解：∵P是BD的中点，E是AB的中点，
∴PE=AD，
同理，PF=BC，
∵AD=BC，
∴PE=PF，
∴∠PFE=×（180°-∠EPF）=16.5°，
故答案为：16.5°．
本题考查的是三角形中位线定理、等腰三角形的性质、三角形内角和定理，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键．
三、解答题（本大题共5个小题，共48分）
14、2（a-b）2
【解析】
先提公因式在利用公式法进行因式分解即可.
【详解】
解：原式=2（a2-2ab+b2）
=2（a-b）2
本题考查的是因式分解，能够熟练运用多种方法进行因式分解是解题的关键.
15、详见解析.
【解析】
先求出不等式组的解集，然后找出其中的整数相加即可.
【详解】
，
解：解不等式①，得x≥-5；
解不等式②，得x