四川省开江县2024年九年级数学第一学期开学学业质量监测模拟试题【含答案】

这是一份四川省开江县2024年九年级数学第一学期开学学业质量监测模拟试题【含答案】，共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米，先到终点的人原地休息．已知甲先出发4分钟，在整个步行过程中，甲、乙两人的距离y（米）与甲出发的时间t（分）之间的关系如图所示，下列结论：①甲步行的速度为60米/分；②乙走完全程用了30分钟；③乙用12分钟追上甲；④乙到达终点时，甲离终点还有360米；其中正确的结论有（ ）
A．1个B．2个C．3个D．4个
2、（4分）在平行四边形ABCD中，，．则平行四边形ABCD的周长是（ ）．
A．16B．13C．10D．8
3、（4分）用配方法解方程时，配方变形结果正确的是（ ）
A．B．C．D．
4、（4分）下列等式成立的是（ ）
A．B．C．D．
5、（4分）下列数据中不能作为直角三角形的三边长是（ ）
A．1、1、B．5、12、13C．3、5、7D．6、8、10
6、（4分）如图 ，在中□ABCD 中，点 E、F 分别在边 AB、CD 上移动，且 AE＝CF，则四边形DEBF 不可能是( )
A．平行四边形B．梯形C．矩形D．菱形
7、（4分）如图，点M是直线y=2x+3上的动点，过点M作MN垂直于x轴于点N，y轴上是否存在点P，使得△MNP为等腰直角三角形，则符合条件的点P有（提示：直角三角形斜边上的中线等于斜边的一半）（ ）
A．2个B．3个C．4个D．5个
8、（4分）一个多边形的内角和是外角和的4倍，则这个多边形的边数是（ ）
A．8B．9C．10D．11
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图，在中，，，以点为圆心，以任意长为半径作弧，分别交、于点、，再分别以点、为圆心，以大于的长为半径作弧，两弧在内交于点，连结并延长，交于点，则的长为____.
10、（4分）如图，已知∠BAC=120º，AB=AC，AC的垂直平分线交BC于点D，则∠ADB=_______；
11、（4分）一次函数不经过第_________象限；
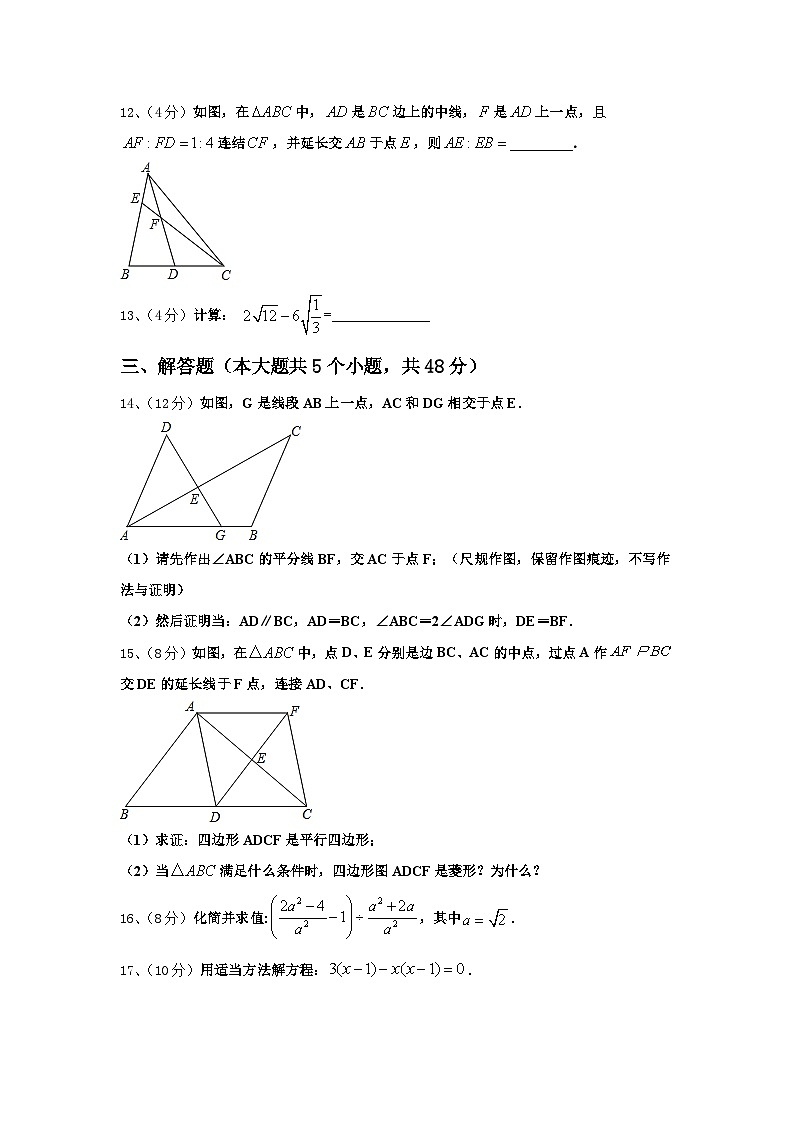
12、（4分）如图，在中，是边上的中线，是上一点，且连结，并延长交于点，则_________.
13、（4分）计算： =______________
三、解答题（本大题共5个小题，共48分）
14、（12分）如图，G是线段AB上一点，AC和DG相交于点E．
（1）请先作出∠ABC的平分线BF，交AC于点F；（尺规作图，保留作图痕迹，不写作法与证明）
（2）然后证明当：AD∥BC，AD＝BC，∠ABC＝2∠ADG时，DE＝BF．
15、（8分）如图，在中，点D、E分别是边BC、AC的中点，过点A作交DE的延长线于F点，连接AD、CF．
（1）求证：四边形ADCF是平行四边形；
（2）当满足什么条件时，四边形图ADCF是菱形？为什么？
16、（8分）化简并求值:，其中.
17、（10分）用适当方法解方程：．
18、（10分）化简并求值：，其中x=﹣1．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）对甲、乙两台机床生产的同一种零件进行抽样检测（抽查的零件个数相同），其平均数、方差的计算结果是：机床甲：，；机床乙：，．由此可知：____（填甲或乙）机床性能较好．
20、（4分）观察以下等式：
第1个等式：
第2个等式：＝1
第3个等式：＝1
第4个等式：＝1
…
按照以下规律，写出你猜出的第n个等式：______(用含n的等式表示)．
21、（4分）若实数a、b满足a＋b＝5，a2b＋ab2＝－10，则ab的值是_______．
22、（4分）已知空气的密度是0.001239，用科学记数法表示为________
23、（4分）如图，某居民小区要一块一边靠墙的空地上建一个长方形花园，花园的中间用平行于的栅栏隔开，一边靠墙，其余部分用总长为米的栅栏围成且面积刚好等于平方米，求围成花园的宽为多少米？设米，由题意可列方程为______．
二、解答题（本大题共3个小题，共30分）
24、（8分）如图，在矩形ABCD中，，点P从点D出发向点A运动，运动到点A即停止；同时，点Q从点B出发向点C运动，运动到点C即停止，点P、Q的速度都是，连接PQ、AQ、设点P、Q运动的时间为ts．
当t为何值时，四边形ABQP是矩形；
当t为何值时，四边形AQCP是菱形．
25、（10分）如图，一次函数的图象与反比例函数（为常数，且）的图象交于A（1，a）、B两点．
（1）求反比例函数的表达式及点B的坐标；
（2）在x轴上找一点P，使PA+PB的值最小，求满足条件的点P的坐标及△PAB的面积．
26、（12分）如图1，正方形ABCD的边长为4厘米，E为AD边的中点，F为AB边上一点，动点P从点B出发，沿B→C→D→E，向终点E以每秒a厘米的速度运动，设运动时间为t秒，△PBF的面积记为S.S与t的部分函数图象如图2所示，已知点M（1，）、N（5，6）在S与t的函数图象上.
（1）求线段BF的长及a的值；
（2）写出S与t的函数关系式，并补全该函数图象；
（3）当t为多少时，△PBF的面积S为4.
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、D
【解析】
根据题意和函数图象中的数据可以判断各个小题中的结论是否正确，从而可以解答本题．
【详解】
解：由题意可得：甲步行速度＝＝60米/分；故①符合题意；
设乙的速度为：x米/分，
由题意可得：16×60＝（16﹣4）x，
解得x＝80
∴乙的速度为80米/分；
∴乙走完全程的时间＝＝30分，
故②符合题意；
由图可得：乙追上甲的时间为（16﹣4）＝12分；
故③符合题意；
乙到达终点时，甲离终点距离是：2400﹣（4+30）×60＝360米，
故④符合题意；
故正确的结论为：①②③④，
故选：D．
本题考查了一次函数的应用，明确题意，读懂函数图像，是解题的关键．
2、A
【解析】
根据平行四边形的性质：平行四边形的对边相等可得DC=5，AD=3，然后再求出周长即可．
【详解】
∵四边形ABCD是平行四边形，
∵AB=CD，AD=BC，
∵AB=5，BC=3，
∴DC=5，AD=3，
∴平行四边形ABCD的周长为：5+5+3+3=16，
故选A．
此题主要考查了平行四边形的性质，关键是掌握平行四边形的对边相等．
3、C
【解析】
根据配方法的步骤先把常数项移到等号的右边，再在等式两边同时加上一次项系数一半的平方，配成完全平方的形式，从而得出答案．
【详解】
∵
∴x2＋6x＝1，
∴x2＋6x＋9＝1＋9，
∴（x＋3）2＝10；
故选：C．
本题考查了配方法解一元二次方程，掌握配方法的步骤是解题的关键；配方法的一般步骤是：
（1）把常数项移到等号的右边；
（2）把二次项的系数化为1；
（3）等式两边同时加上一次项系数一半的平方．
4、B
【解析】
根据二次根式的加减、乘除运算法则以及二次根式的性质解答即可．
【详解】
解：A. 不是同类二次根式，故A错误；
B. ，故B正确；
C. ，故B错误；
D. ，故D错误．
故答案为B．
本题考查了二次根式的加减、乘除运算法则以及二次根式的性质，牢记并灵活运用运算法则和性质是解答本题的关键．
5、C
【解析】
解：A、，能构成直角三角形，故选项错误；
B、52+122=132，能构成直角三角形，故选项错误；
C、32+52≠72，不能构成直角三角形，故选项正确；
D、62+82=102，能构成直角三角形，故选项错误．
故选C．
6、B
【解析】
由于在平行四边形ABCD中AB=CD，而AE=CF，由此可以得到BE=DF，根据平行四边形的判定方法即可判定其实平行四边形，所以不可能是梯形．
【详解】
解：∵四边形ABCD是平行四边形，
∴AB=CD，AB∥CD，
又AE=CF，
∴BE=DF，
∴四边形BEDF是平行四边形，所以不可能是梯形．
故选：B．
本题考查平行四边形的性质，注意：一组对边平行，一组对角相等的四边形是平行四边形；一组对边平行，另一组对边相等的四边形不一定是平行四边形，如：等腰梯形．
7、C
【解析】
根据等腰直角三角形的定义,由题意,应分两类情况讨论：当MN为直角边时和当MN为斜边时点Ｐ的位置的求法．
【详解】
当M运动到(－1，1)时，ON=1，MN=1，
∵MN⊥x轴，所以由ON=MN可知，(0，0)和(0，1)就是符合条件的P点；
又当M运动到第三象限时，要MN=MP，且PM⊥MN，设点M(x，2x+3)，则有－x=－(2x+3)，解得x=－3，所以点P坐标为(0，－3)．
如若MN为斜边时，则∠ONP=45°，所以ON=OP，设点M(x，2x+3)，则有－x=－(2x+3)，化简得－2x=－2x－3，这方程无解，所以这时不存在符合条件的P点；
又当点M′在第二象限，M′N′为斜边时，这时N′P=M′P，∠M′N′P=45°，设点M′(x，2x+3)，则OP=ON′，而OP=M′N′，∴有－x=(2x+3)，解得x=－，这时点P的坐标为(0，－)．
因此，符合条件的点P坐标是(0，0)，(0，－)，(0，－3)，(0，1)．
故答案选C,
本题主要采用分类讨论法,来求得符合条件的点P坐标．题中没有明确说明哪个边是直角边,哪条边是斜边,所以分情况说明,在证明时,注意点M的坐标表示方法以及坐标与线段长之间的转换.
8、C
【解析】
利用多边形的内角和公式及外角和定理列方程即可解决问题．
【详解】
设这个多边形的边数是n，
则有（n-2）×180°=360°×4，
所有n=1．
故选C．
熟悉多边形的内角和公式：n边形的内角和是（n-2）×180°；多边形的外角和是360度．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、1.
【解析】
根据作图过程可得得AE平分∠ABC；再根据角平分线的性质和平行四边形的性质可证明∠AEB=∠CBE，证出AE=AB=3，即可得出DE的长．，
【详解】
解：根据作图的方法得：AE平分∠ABC，
∴∠ABE=∠CBE
∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC=5，
∴∠AEB=∠CBE，
∴∠ABE=∠AEB，
∴AE=AB=3，
∴DE=AD﹣AE=5﹣3=1；
故答案为：1．
此题考查了平行四边形的性质、等腰三角形的判定．熟练掌握平行四边形的性质，证出AE=AB是解决问题的关键．
10、60
【解析】
先根据等腰三角形的性质求出∠C的度数，再由线段垂直平分线的性质可知∠C=∠CAD，根据三角形内角与外角的关系即可求解．
【详解】
解：∵∠BAC=120°，AB=AC，
∴∠C= ==30°，
∵AC的垂直平分线交BC于D，
∴AD=CD，
∴∠C=∠CAD=30°，
∵∠ADB是△ACD的外角，
∴∠ADB=∠C+∠CAD=30°+30°=60°．
故答案为60°．
本题主要考查线段垂直平分线的性质，等腰三角形的性质，熟记知识点是解题的关键．
11、三
【解析】
根据一次函数的图像与性质即可得出答案.
【详解】
∵一次函数解析式为：y=-x+1
其中k=-10
∴函数图像经过一、二、四象限，不经过第三象限
故答案为：三.
本题考查的是一次函数的图像与性质，熟练掌握一次函数的图像与性质是解决本题的关键.
12、1：8.
【解析】
先过点D作GD∥EC交AB于G，由平行线分线段成比例可得BG=GE，再根据GD∥EC，得出AE=，最后根据AE：EB=：2EG，即可得出答案．
【详解】
过点D作GD∥EC交AB于G，
∵AD是BC边上中线，
∴，即BG=GE，
又∵GD∥EC，
∴，
∴AE=，
∴AE：EB=：2EG=1：8.
故答案为：1：8.
本题主要考查了平行线分线段成比例定理，用到的知识点是平行线分线段成比例定理，关键是求出AE、EB、EG之间的关系．
13、2
【解析】
先将二次根式化为最简，然后合并同类二次根式即可．
【详解】
解：原式=．
故答案为：2．
本题考查了二次根式的加减运算，掌握二次根式的化简及同类二次根式的合并是关键．
三、解答题（本大题共5个小题，共48分）
14、（1）见解析；（2）见解析.
【解析】
（1）根据角平分线的作图方法作图即可；
（2）由题意易证△ADE≌△CBF推出DE＝BF．
【详解】
（1）解：以B为圆心、适当长为半径画弧，交AB、BC于M、N两点，分别以M、N为圆心、大于MN长为半径画弧，两弧相交于点P，过B、P作射线BF交AC于F．

（2）证明如下：∵AD∥BC，∴∠DAC＝∠C．
∵BF平分∠ABC，∴∠ABC＝2∠FBC，
又∵∠ABC＝2∠ADG，∴∠D＝∠FBC，
在△ADE与△CBF中，，
∴△ADE≌△CBF（ASA），
∴DE＝BF．
本题考查的是全等三角形的判定定理以及基本作图的有关知识，难度一般．
15、（1）见解析；（2）当△ABC是直角三角形，且∠BAC=90°时，四边形ADCF是菱形，理由见解析．
【解析】
（1）首先利用平行四边形的判定方法得出四边形ABDF是平行四边形，进而得出AF=DC，利用一组对边相等且平行的四边形是平行四边形，进而得出答案；
（2）利用直角三角形的性质结合菱形的判定方法得出即可．
【详解】
（1）证明：∵点D、E分别是边BC、AC的中点，
∴DE∥AB，BD=CD，
∵AF∥BC，
∴四边形ABDF是平行四边形，
∴AF=BD，则AF=DC，
∵AF∥BC，
∴四边形ADCF是平行四边形；
（2）解：当△ABC是直角三角形，且∠BAC=90°时，四边形ADCF是菱形，
理由：∵△ABC是直角三角形，且∠BAC=90°
又∵点D是边BC的中点，
∴AD=DC，
∴平行四边形ADCF是菱形．
本题考查平行四边形的判定与性质以及菱形的判定，熟练应用平行四边形的判定与性质是解题关键．
16、，
【解析】
首先进行化简，在代入计算即可.
【详解】
原式
当时，原式
本题主要考查根式的化简，注意根式的分母不等为0，这是必考题，必须掌握.
17、，
【解析】
利用分解因式法求解即可．
【详解】
解：原方程可化为：，
∴或，
解得：，．
本题考查的是一元二次方程的解法，属于基础题型，熟练掌握分解因式的方法是解题的关键．
18、2.
【解析】
试题分析：先将进行化简，再将x的值代入即可;
试题解析：
原式=﹣•（x﹣1）==，
当x=﹣1时，原式=﹣2．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、甲
【解析】
试题解析：∵S2甲＜S2乙，
∴甲机床的性能较好．
点睛：方差反映了一组数据的波动大小，方差越大，波动性越大，反之也成立．
20、++×＝1
【解析】
观察前四个等式可得出第n个等式的前两项为及，对比前四个等式即可写出第n个等式，此题得解．
【详解】
解：观察前四个等式，可得出：第n个等式的前两项为及，

∴第n个等式为
故答案为：++×＝1
本题考查规律型中的数字的变化类，观察给定等式，找出第n的等式是解题的关键．
21、－1
【解析】
先提取公因式ab，整理后再把a+b的值代入计算即可．
【详解】
解：a+b=5时，
原式=ab（a+b）=5ab=-10，
解得：ab=-1．
故答案为：-1.
本题考查了提公因式法分解因式，提取公因式后整理成已知条件的形式是解本题的关键，也是难点．
22、1.239×10-3.
【解析】
绝对值小于1的数也可以利用科学记数法表示，一般形式为a×10-n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．
【详解】
0.001239=1.239×10-3
故答案为：1.239×10-3.
本题考查了科学记数法的表示，熟练掌握n的值是解题的关键.
23、
【解析】
根据题意设AB=x米，则BC=（30-3x）m，利用矩形面积得出答案．
【详解】
解：设AB=x米，由题意可列方程为：x（30-3x）=1．
故答案为：x（30-3x）=1．
此题主要考查了由实际问题抽象出一元二次方程，正确表示出BC的长是解题关键．
二、解答题（本大题共3个小题，共30分）
24、当时，四边形ABQP为矩形； 当时，四边形AQCP为菱形．
【解析】
当四边形ABQP是矩形时，，据此求得t的值；
当四边形AQCP是菱形时，，列方程求得运动的时间t；
【详解】
由已知可得，，
在矩形ABCD中，，，
当时，四边形ABQP为矩形，
，得
故当时，四边形ABQP为矩形．
由可知，四边形AQCP为平行四边形
当时，四边形AQCP为菱形
即时，四边形AQCP为菱形，解得，
故当时，四边形AQCP为菱形．
本题考查了菱形、矩形的判定与性质解决此题注意结合方程的思想解题．
25、（1），；（2）P，．
【解析】
试题分析：（1）由点A在一次函数图象上，结合一次函数解析式可求出点A的坐标，再由点A的坐标利用待定系数法即可求出反比例函数解析式，联立两函数解析式成方程组，解方程组即可求出点B坐标；
（2）作点B作关于x轴的对称点D，交x轴于点C，连接AD，交x轴于点P，连接PB．由点B、D的对称性结合点B的坐标找出点D的坐标，设直线AD的解析式为y=mx+n，结合点A、D的坐标利用待定系数法求出直线AD的解析式，令直线AD的解析式中y=0求出点P的坐标，再通过分割图形结合三角形的面积公式即可得出结论．
试题解析：（1）把点A（1，a）代入一次函数y=-x+4，
得：a=-1+4，解得：a=3，
∴点A的坐标为（1，3）．
把点A（1，3）代入反比例函数y=，
得：3=k，
∴反比例函数的表达式y=，
联立两个函数关系式成方程组得：，
解得：，或，
∴点B的坐标为（3，1）．
（2）作点B作关于x轴的对称点D，交x轴于点C，连接AD，交x轴于点P，此时PA+PB的值最小，连接PB，如图所示．
∵点B、D关于x轴对称，点B的坐标为（3，1），
∴点D的坐标为（3，- 1）．
设直线AD的解析式为y=mx+n，
把A，D两点代入得：，
解得：，
∴直线AD的解析式为y=-2x+1．
令y=-2x+1中y=0，则-2x+1=0，
解得：x=，
∴点P的坐标为（，0）．
S△PAB=S△ABD-S△PBD=BD•（xB-xA）-BD•（xB-xP）
=×[1-（-1）]×（3-1）-×[1-（-1）]×（3-）
=．
考点：1.反比例函数与一次函数的交点问题；2.待定系数法求一次函数解析式；3.轴对称-最短路线问题．
26、 (1)BF=3，a=1；（2）当0≤t≤4时，S=t；当4＜t≤8时，S=6；当8＜t≤10时，S=18-t.图像见解析；（3）t=或.
【解析】
试题分析：（1）根据图2可以看出，当t=5时，P在CD上，此时△PBF的高就为正方形的边长，底为BF，利用面积等于6，可求得BF，再根据t=1时，△PBF的面积为，可求得a的值；（2）由点P运动过程，可发现△PBF的面积有3种情况，分别是：当0≤t≤4时，此时P在AB上，当4＜t≤8时，此时P在CD上，当8＜t≤10时，此时P在AD上，分别求出解析式即可.再根据解析式可补全图像；（3）把S=4分别代入解析式中即可求出t值.
试题解析：（1）由题意可知，当t=5时，S△PBF=×4BF=6，BF=3.当t=1时，S△PBF=at×3=，a=1；（2）当0≤t≤4时，设S=kt，把（1，）代入得，k=，S=t；当4＜t≤8时，S=6；当8＜t≤10时，设S=mt+b，把（8,6），（10,3）代入，得，解得，S=18-t.综上所述，当0≤t≤4时，S=t；当4＜t≤8时，S=6；当8＜t≤10时，S=18-t，据此可补全图像，如下图：
（3）当S＝4时，t＝4，t＝；18－t＝4，t＝.∴当t＝或 t＝时△PBF的面积S为4.
考点：1分段函数；2分类讨论；3数形结合.
题号
一
二
三
四
五
总分
得分