苏州市振华中学2024年数学九上开学经典模拟试题【含答案】

这是一份苏州市振华中学2024年数学九上开学经典模拟试题【含答案】，共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）若，则下列不等式一定成立的是（ ）.
A．B．C．D．
2、（4分）要使式子有意义，则的取值范围是（ ）
A．B．C．D．
3、（4分）已知A、C两地相距40千米，B、C两地相距50千米，甲乙两车分别从A、B两地同时出发到C地．若乙车每小时比甲车多行驶12千米，则两车同时到达C地．设乙车的速度为x千米/小时，依题意列方程正确的是（ ）
A．B．C．D．
4、（4分）把一些笔记本分给几个学生，如果每人分3本，那么余8本，如果每人分5本，则最后一个人分到的本数不足3本，则共有学生( )人．
A．4 B．5 C．6 D．5或6
5、（4分）如图，在平行四边形ABCD中，对角线AC、BD相交于点O，且OA=OB，若AD=4，，则AB的长为（ ）
A．B．C．8D．
6、（4分）若式子在实数范围内有意义，则x的取值范围是（ ）
A．x≥B．x＞C．x≥D．x＞
7、（4分）若分式方程+3＝有增根，则a的值是（ ）
A．﹣1B．0C．1D．2
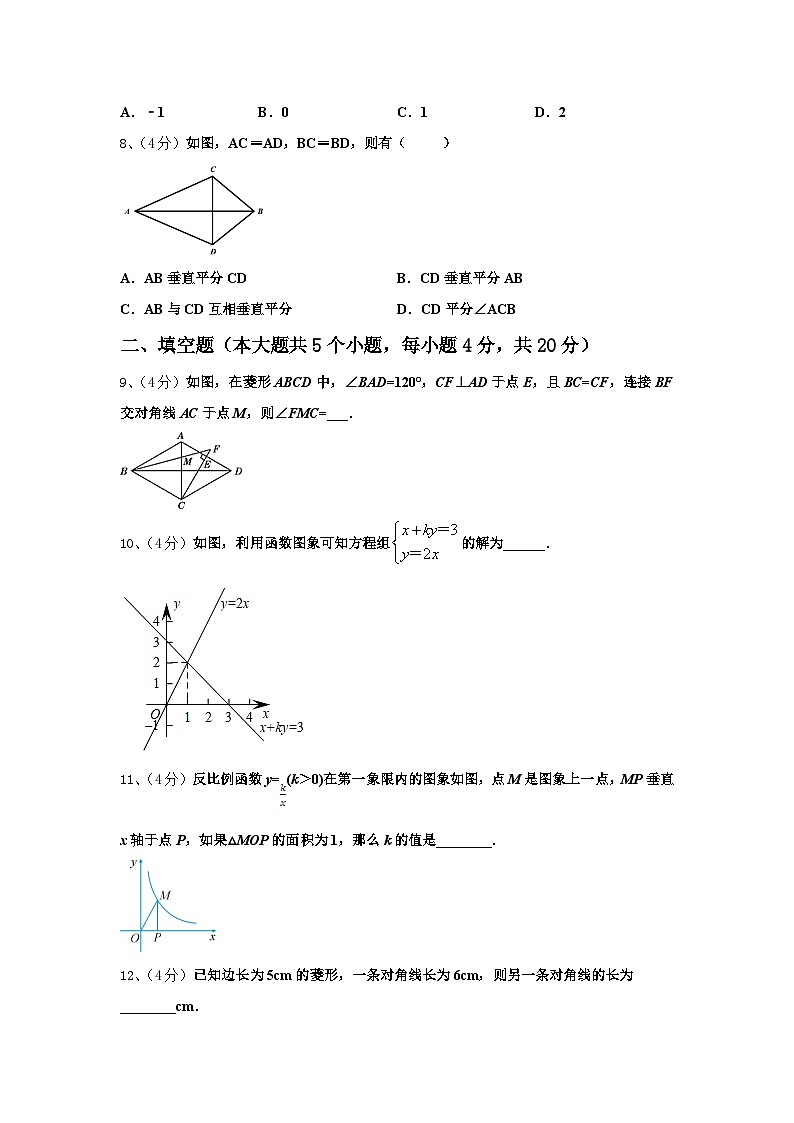
8、（4分）如图，AC＝AD，BC＝BD，则有（ ）
A．AB垂直平分CDB．CD垂直平分AB
C．AB与CD互相垂直平分D．CD平分∠ACB
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图，在菱形ABCD中，∠BAD=120°，CF⊥AD于点E，且BC=CF，连接BF交对角线AC于点M，则∠FMC=___．
10、（4分）如图，利用函数图象可知方程组的解为______．
11、（4分）反比例函数y=(k＞0)在第一象限内的图象如图，点M是图象上一点，MP垂直x轴于点P，如果△MOP的面积为1，那么k的值是________.
12、（4分）已知边长为5cm的菱形，一条对角线长为6cm，则另一条对角线的长为________cm．
13、（4分）在平面直角坐标系中，若直线y=kx+b经过第一、三、四象限，则直线y=bx+k不经过的象限是________．
三、解答题（本大题共5个小题，共48分）
14、（12分）某蛋糕店为了吸引顾客，在A、B两种蛋糕中，轮流降低其中一种蛋糕价格，这样形成两种盈利模式，模式一：A种蛋糕利润每盒8元，B种蛋糕利润每盒15元；模式二：A种蛋糕利润每盒14元，B种蛋糕利润每盒11元每天限定销售A、B两种蛋糕共40盒，且都能售完，设每天销售A种蛋糕x盒
（1）设按模式一销售A、B两种蛋糕所获利润为y1元，按模式二销售A、B两种蛋糕所获利润为y2元，分别求出y1、y2关于x的函数解析式；
（2）在同一个坐标系内分别画出(1)题中的两个函数的图象；
（3）若y始终表示y1、y2中较大的值，请问y是否为x的函数，并说说你的理由，并直接写出y的最小值．
15、（8分）（1）如图，在平行四边形中，过点作 于点 ，交 于点 ，过点 作 于点 ，交 于点 .
①求证：四边形 是平行四边形；
②已知，求的长.
（2）已知函数.
①若函数图象经过原点，求的值
②若这个函数是一次函数，且随着的增大而减小，求的取值范围
16、（8分）某校学生会在得知田同学患重病且家庭困难时，特向全校3000名同学发起“爱心”捐款活动，为了解捐款情况，学生会随机调查了该校某班学生的捐款情况，并将得到的数据绘制成如下两个统计图，请根据相关信息解答下列问题．
（1）该班的总人数为 ______ 人，将条形图补充完整；
（2）样本数据中捐款金额的众数 ______ ，中位数为 ______ ；
（3）根据样本数据估计该校3000名同学中本次捐款金额不少于20元有多少人？
17、（10分）（知识背景）
据我国古代《周髀算经》记载，公元前1120年商高对周公说，将一根直尺折成一个直角，两端连接得到一个直角三角形，如果勾是3，股是4，那么弦就等于5，后人概括为“勾三、股四、弦五”．像3、4、5这样为三边长能构成直角三角形的三个正整数，称为勾股数．
（应用举例）
观察3，4，5；5，12，13；7，24，25；…
可以发现这些勾股数的勾都是奇数，且从3起就没有间断过，并且
勾为3时，股，弦；
勾为5时，股，弦；
请仿照上面两组样例，用发现的规律填空：
（1）如果勾为7，则股24＝ 弦25＝
（2）如果勾用（，且为奇数）表示时，请用含有的式子表示股和弦，则股＝ ，弦＝ ．
（解决问题）
观察4，3，5；6，8，10；8，15，17；…根据应用举例获得的经验进行填空：
（3）如果是符合同样规律的一组勾股数，（表示大于1的整数），则 ， ，这就是古希腊的哲学家柏拉图提出的构造勾股数组的公式．
（4）请你利用柏拉图公式，补全下面两组勾股数（数据从小到大排列）第一组： 、24、 ：第二组： 、 、1．
18、（10分）如图，已知过点B（1，0）的直线与直线：相交于点P（－1，a）．且l1与y轴相交于C点，l2与x轴相交于A点．
（1）求直线的解析式；
（2）求四边形的面积；
（3）若点Q是x轴上一动点，连接PQ、CQ，当△QPC周长最小时，求点Q坐标．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）如图，已知△ABC中，AC=BC，∠ACB=90°，直角∠DFE的顶点F是AB中点，两边FD，FE分别交AC，BC于点D，E两点，当∠DFE在△ABC内绕顶点F旋转时（点D不与A，C重合），给出以下个结论：①CD=BE；②四边形CDFE不可能是正方形；③△DFE是等腰直角三角形；④S四边形CDFE=S△ABC．上述结论中始终正确的有______．（填序号）
20、（4分）把二次根式化成最简二次根式，则=____．
21、（4分）如图，在矩形ABCD，BE平分，交AD于点E，F是BE的中点，G是BC的中点，连按EC，若，，则FG的长为________。
22、（4分）已知关于的方程有解，则的值为____________．
23、（4分）与最简二次根式是同类二次根式，则__________．
二、解答题（本大题共3个小题，共30分）
24、（8分）如图，平行四边形ABCD中，对角线AC，BD相交于点O，点E，F分别是OB，OD的中点．
（1）试说明四边形AECF是平行四边形．
（2）若AC＝2，AB＝1．若AC⊥AB，求线段BD的长．
25、（10分）如图，在四边形OABC中，OA∥BC，∠OAB=90°，O为原点，点C的坐标为(2，8)，点A的坐标为(26，0)，点D从点B出发，以每秒1个单位长度的速度沿BC向点C运动，点E同时从点O出发，以每秒3个单位长度的速度沿折线OAB运动，当点E达到点B时，点D也停止运动，从运动开始，设D(E)点运动的时间为t秒．
(1)当t为何值时，四边形ABDE是矩形；
(2)当t为何值时，DE=CO？
(3)连接AD，记△ADE的面积为S，求S与t的函数关系式．
26、（12分）如图，菱形中，为对角线的延长线上一点.
（1）求证：；
（2）若，，，求的长.
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、C
【解析】
按照不等式的性质逐项排除即可完成解答.
【详解】
∵x＞y
∴，A错误；
3x>3y，B错误；
,即C正确；
，错误；
故答案为C;
本题考查了不等式的基本性质，即给不等式两边同加或减去一个整数，不等号方向不变；给不等式两边同乘以一个正数，不等号方向不变；给不等式两边同乘以一个负数，不等号方向改变；
2、D
【解析】
根据二次根式被开方数必须是非负数的条件，要使在有意义，必须.
故选D.
3、B
【解析】
试题解析：设乙车的速度为x千米/小时，则甲车的速度为（x-12）千米/小时，
由题意得，．
故选B．
4、C
【解析】
根据每人分3本，那么余8本，如果前面的每个学生分1本，那么最后一人就分不到3本，得出3x+8≥1（x-1），且1（x-1）+3＞3x+8，分别求出即可．
【详解】
假设共有学生x人，根据题意得出：
1（x-1）+3＞3x+8≥1（x-1），
解得：1＜x≤6.1．
故选：C．
本题考查了不等式组的应用，解题关键是根据题意找出不等关系得出不等式组．
5、A
【解析】
由平行四边形ABCD中，OA=OB得到平行四边形ABCD是矩形，又，得到三角形AOD为等边三角形，再利用勾股定理得到AB的长.
【详解】
解：∵四边形ABCD为平行四边形，对角线AC、BD相交于点O，
∴OA=OC，OB=OD，
又∵OA=OB，
∴OA=OD=OB=OC，
∴平行四边形ABCD为矩形，∠DAB=90°,
而，
∴为等边三角形，
∴AD=OD=OA=OB=4，
在Rt中，AD=4，DB=2OD=8，
∴,
故选：A.
本题利用了矩形的判定和性质，等边三角形的判定及性质，勾股定理定理的应用求解．属于基础题.
6、A
【解析】
根据：二次根式的被开方数必须大于或等于0，才有意义.
【详解】
若式子在实数范围内有意义，则2x-3≥0,即x≥.
故选A
本题考核知识点：二次根式有意义问题.解题关键点：熟记二次根式有意义条件.
7、B
【解析】
根据分式方程有增根可得出x=2是方程1+3（x-2）=a+1的根，代入x=2即可求出a值．
【详解】
解：∵分式方程+3＝有增根，
∴x=2是方程1+3（x-2）=a+1的根，
∴a=1．
故选：B．
本题考查分式方程的增根，熟记分式方程增根的定义是解题的关键．
8、A
【解析】
由AC＝AD，BC＝BD，可得点A在CD的垂直平分线上，点B在CD的垂直平分线上，又由两点确定一条直线，可得AB是CD的垂直平分线．
【详解】
解：∵AC＝AD，BC＝BD，
∴点A在CD的垂直平分线上，点B在CD的垂直平分线上，
∴AB是CD的垂直平分线．
即AB垂直平分CD．
故选：A．
此题考查了线段垂直平分线的性质．此题难度不大，注意掌握数形结合思想的应用．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、1°
【解析】
利用菱形的性质得出∠BCA=60°，∠ACE=∠DCE=30°，∠CBD=∠ABD=30°，AC⊥BD，再利用等腰三角形的性质以及三角形外角的性质得出答案．
【详解】
∵菱形ABCD中，∠BAD=120°，CF⊥AD于点E，
∴∠BCA=60°，∠ACE=∠DCE=30°，∠CBD=∠ABD=30°，AC⊥BD，
∴∠BCF=90°，
∵BC=CF，
∴∠CBF=∠BFC=45°，
∴∠FBD=45°-30°=15°，
∴∠FMC=90°+15°=1°．
故答案为：1．
此题考查菱形的性质，等腰三角形的性质，得出∠CBF=∠BFC=45°是解题关键．
10、
【解析】
观察函数的图象y=2x与x+ky=3相交于点（1，2），从而求解；
【详解】
观察图象可知，y=2x与x+ky=3相交于点（1，2），
可求出方方程组的解为，
故答案为：
此题主要考查一次函数与二元一次方程组，关键是能根据函数图象的交点解方程组．
11、1
【解析】
过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值，即S=|k|．
【详解】
解：由题意得：S△MOP=|k|=1，k=±1，
又因为函数图象在一象限，所以k=1．
故答案为：1.
主要考查了反比例函数y＝中k的几何意义，即过双曲线上任意一点引x轴、y轴垂线，所得三角形面积为|k|，是经常考查的一个知识点；这里体现了数形结合的思想，做此类题一定要正确理解k的几何意义．
12、8
【解析】
根据菱形的对角线互相垂直平分，得已知对角线的一半是1．根据勾股定理，得要求的对角线的一半是4，则另一条对角线的长是8.
【详解】
解：在菱形ABCD中，AB=5，AC=6，
因为对角线互相垂直平分，
所以∠AOB=90°，AO=1，
在RT△AOB中，BO=，
∴BD=2BO=8.
注意菱形对角线的性质：菱形的对角线互相垂直平分．熟练运用勾股定理．
13、第三象限
【解析】分析：
根据直线y=kx+b在平面直角坐标系中所经过象限与k、b值的关系进行分析解答即可.
详解：
∵直线y=kx+b经过第一、三、四象限，
∴k>0，b