安徽省六安市裕安区青山路初级中学2024-2025学年九年级上学期第一次月考数学试卷

这是一份安徽省六安市裕安区青山路初级中学2024-2025学年九年级上学期第一次月考数学试卷，共16页。试卷主要包含了选择题每小题都给出A，填空题等内容，欢迎下载使用。
1．（4分）下列函数是二次函数的是（ ）
A．B．C．y＝3x+2D．
2．（4分）抛物线y＝﹣3（x+2）2+1的顶点坐标是（ ）
A．（2，1）B．（﹣2，﹣1）C．（﹣2，1）D．（2，﹣1）
3．（4分）抛物线y＝2x2向右平移1个单位，再向下平移2个单位，所得到的抛物线是（ ）
A．y＝2（x﹣1）2﹣2B．y＝2（x+1）2﹣2
C．y＝2（x+1）2+2D．y＝2（x﹣1）2+2
4．（4分）二次函数y＝3（x﹣2）2的图象的对称轴是（ ）
A．直线x＝0B．直线x＝3C．直线x＝﹣2D．直线x＝2
5．（4分）下列二次函数解析式中，其图象与y轴的交点在x轴下方的是（ ）
A．y＝x2+3B．y＝x2﹣3C．y＝﹣x2+3D．y＝x2
6．（4分）在函数y＝﹣（x﹣3）2+1的图象上，当y随x的增大而减小时，x的取值范围为（ ）
A．x≥3B．x≤3C．x≥1D．x≤1
7．（4分）二次函数y＝ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如下表：
则代数式的值为（ ）
A．2.5B．3.5C．8.5D．﹣3.5
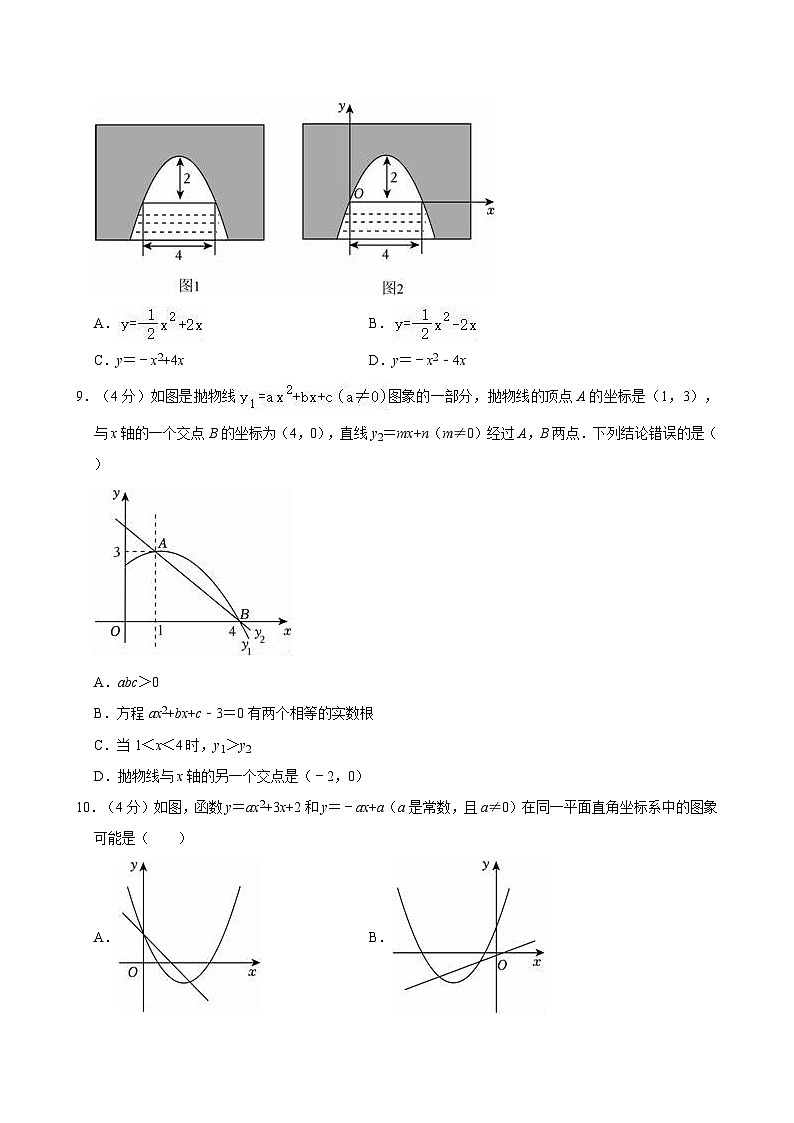
8．（4分）如图1是抛物线形石拱桥，当水面离拱顶2m时，水面宽4m．建立如图2所示的平面直角坐标系，则抛物线的表达式为（ ）
A．B．
C．y＝﹣x2+4xD．y＝﹣x2﹣4x
9．（4分）如图是抛物线图象的一部分，抛物线的顶点A的坐标是（1，3），与x轴的一个交点B的坐标为（4，0），直线y2＝mx+n（m≠0）经过A，B两点．下列结论错误的是（ ）
A．abc＞0
B．方程ax2+bx+c﹣3＝0有两个相等的实数根
C．当1＜x＜4时，y1＞y2
D．抛物线与x轴的另一个交点是（﹣2，0）
10．（4分）如图，函数y＝ax2+3x+2和y＝﹣ax+a（a是常数，且a≠0）在同一平面直角坐标系中的图象可能是（ ）
A．B．
C．D．
二、填空题（本大题共4小题，每小题5分，满分20分）
11．（5分）若二次函数y＝（m﹣3）x2+（m+1）x﹣m+1的图象经过原点，则m的值为 ．
12．（5分）把二次函数y＝x2+bx+3由一般式化成顶点式为y＝（x+2）2+k，则k的值为 ．
13．（5分）若抛物线y＝ax2的图象与一次函数y＝bx+c的图象有两个交点，分别为（﹣2，8），（1，2），则关于x的方程ax2﹣bx﹣c＝0的解为 ．
14．（5分）如图，在平面直角坐标系中，点A（8，0），点B（0，4），点M为OA上一点，过点M作CM⊥BM，且CM＝BM，连接AC．
（1）当点M为OA的中点时，AC的长为 ．
（2）当点M在OA上移动时，AC的最小值为 ．
三、（本大题共2小题，每小题0分，满分0分）
15．已知二次函数y＝x2+bx+c的图象经过点（﹣1，0），（1，﹣2），求该二次函数的表达式．
16．已知抛物线与直线y2＝x+6的图象交于A，B两点（点A在点B的左侧），试分别求A，B两点的横坐标．
四、（本大题共2小题，每小题8分，满分16分）
17．（8分）已知抛物线y＝﹣3x2+6x+4．
（1）求该抛物线的开口方向、对称轴及顶点坐标；
（2）当x为何值时，y随x的增大而减小，当x为何值时，y随x的增大而增大？
18．（8分）如图是学校校园内一堵围墙边上的一块空地，现准备用木栏围成一个矩形菜园ABCD作为学生的实践基地．已知矩形菜园的一边AD靠墙（墙足够长），另三边一共用了100m木栏．请设计一个修建方案，使得矩形菜园的面积最大．
五、（本大题共2小题，每小题10分，满分20分）
19．（10分）已知二次函数y＝﹣x2+bx+c的图象的顶点为（2，3）．
（1）求b，c的值；
（2）当y≤﹣1时，求x的取值范围．
20．（10分）已知二次函数y＝﹣x2+2x﹣m（m是常数）．
（1）若该二次函数的图象与x轴有两个不同的交点，求m的取值范围；
（2）若该二次函数的图象与x轴的其中一个交点坐标为（﹣1，0），求一元二次方程﹣x2+2x﹣m＝0的解．
六、（本题满分12分）
21．（12分）如图，点A在x轴的正半轴上，且OA＝4，点B在y轴的正半轴上，且OB＝6，直线AB与抛物线y＝ax2﹣1在第一象限内相交于点P，连接OP，已知S△OAP＝6．
（1）求a的值；
（2）若将抛物线y＝ax2﹣1先向右平移2个单位，再向下平移t（t＞0）个单位，恰好经过点A，试确定t的值．
七、（本题满分12分）
22．（12分）又到了板栗飘香的季节，为提高大家购买的积极性，销售板栗的顺发果业每天拿出2000元现金，作为红包发给购买者．已知板栗每日销售量y（kg）与销售单价x（元/kg）满足关系：y＝﹣100x+4000．当每日销售量低于3000kg时，成本价格为6元/kg；当每日销售量不低于3000kg时，成本价格为5元/kg；在销售中销售单价不低于成本价格且不高于30元/kg．设销售板栗的日获利为w（元）．
（1）当日销售量不低于3000kg时，x的取值范围是 ；
（2）请求出日获利w与销售单价x之间的函数关系式；
（3）当销售单价定为多少时，销售这种板栗日获利最大？最大利润为多少元？
八、（本题满分14分）
23．（14分）如图，抛物线y＝ax2+bx+5（a≠0）与x轴交于A（5，0），C（﹣1，0）两点，交y轴于点B．
（1）求抛物线的表达式；
（2）点P是第一象限内抛物线上的一点，过点P作直线PD⊥x轴于点D，交直线AB于点E．
①当PE＝DE时，求点E的坐标；
②当PE取得最大值时，求点P的坐标．
2024-2025学年安徽省六安市裕安区青山路中学九年级（上）第一次月考数学试卷
参考答案与试题解析
一、选择题（本大题共10小题，每小题4分，满分40分）每小题都给出A、B、C、D四个选项，其中只有一个是符合题目要求的。
1．【解答】解：A、，不是二次函数，故本选项错误，不符合题意；
B、，是二次函数，故本选项正确，符合题意；
C、y＝3x+2，是一次函数，故本选项错误，不符合题意；
D、，不是二次函数，故本选项错误，不符合题意；
故选：B．
2．【解答】解：∵抛物线y＝﹣3（x+2）2+1，
∴当x+2＝0时，y＝1，
∴抛物线y＝﹣3（x+2）2+1的顶点坐标是（﹣2，1），
故选：C．
3．【解答】解：抛物线y＝2x2向右平移1个单位，再向下平移2个单位，
得到的抛物线是：y＝2（x﹣1）2﹣2．
故选：A．
4．【解答】解：∵顶点式y＝a（x﹣h）2+k，顶点坐标是（h，k），对称轴是直线x＝h，
∴顶点坐标为（2，0），
∴对称轴为x＝2，
故选：D．
5．【解答】解：A、令x＝0，得y＝3，则抛物线y＝x2+3与y轴的交点坐标为（0，3），所以A选项错误；
B、令x＝0，得y＝﹣3，则抛物线y＝x2﹣3与y轴的交点坐标为（0，﹣3），所以B选项正确；
C、令x＝0，得y＝3，则抛物线y＝﹣x2+3与y轴的交点坐标为（0，3），所以C选项错误；
D、令x＝0，得y＝0，则抛物线y＝x2与y轴的交点坐标为（0，0），所以D选项错误．
故选：B．
6．【解答】解：函数y＝﹣（x﹣3）2+1的图象上，k＜0，
∴开口向下，顶点为（3，1），
∴当x≤3时，y随x的增大而增大，当x≥3时，y随x的增大而减小，
故选：A．
7．【解答】解：当x＝1时，y＝a+b+c＝5，
当x＝0时，y＝3；当x＝3时，y＝3，
∴二次函数图象的对称轴为，
∴，
∴a+b+c+＝5+（﹣1.5）＝3.5．
故选：B．
8．【解答】解：由图可知，二次函数图象经过（0，0），（4，0），设二次函数解析式为y＝a（x﹣0）（x﹣4），
∵顶点坐标为（2，2），代入y＝a（x﹣0）（x﹣4）得：
2＝a（2﹣0）（2﹣4），
解得，
∴二次函数解析式为x，
故选：A．
9．【解答】解：由题意，∵二次函数图象开口向下，
∴a〈0．
又∵抛物线与y轴的交于正半轴，
∴c〉0．
∵顶点坐标为A（1，3），
∴对称轴为直线，
∴b＝﹣2a＞0，
∴abc＜0．
∴A选项错误，符合题意；
∵顶点坐标为A（1，3），
∴当x＝1时，．
∴ax2+bx+c﹣3＝0有两个相等的实数根，x1＝x2＝1，故B选项正确，不符合题意；
根据图示可得，当1＜x＜4时，y1＞y2，故C选项正确，不符合题意；
∵二次函数的对称轴为x＝1，与x轴的一个交点坐标为（4，0），
∴另一个交点的横坐标为x＝1×2﹣4＝﹣2，
∴抛物线与x轴的另一个交点是（﹣2，0），故D选项正确，不符合题意；
故选：A．
10．【解答】解：当a＞0时，则﹣a＜0，
∴一次函数y＝﹣ax+a的图象经过第一、二、四象限；
二次函数y＝ax2+3x+2的图象开口向上，对称轴为，即对称轴在y轴的左边，当x＝0时，y＝2，即与y轴交于点（0，2）；
A、B、C、D选项均不符合该种情况；
当a＜0时，﹣a＞0，
∴一次函数图象经过第一、三、四象限；
二次函数图象开口向下，对称轴，即对称轴在y轴右边，与y轴交于点（0，2）；
如图所示，
∴D选项的图符合题意，
故选：D．
二、填空题（本大题共4小题，每小题5分，满分20分）
11．【解答】解：∵二次函数经过原点（0，0），
∴﹣m+1＝0，且m﹣3≠0，
解得，m＝1，m≠3，
∴m的值为1，
故答案为：1．
12．【解答】解：∵二次函数y＝x2+bx+3由一般式化成顶点式为y＝（x+2）2+k，
而，
∴，
解得：b＝4，
∴，
故答案为：﹣1．
13．【解答】解：由得ax2＝bx+c，
整理得ax2﹣bx﹣c＝0，
∵抛物线y＝ax2与直线y＝bx+c有两个交点，分别为（﹣2，8），（1，2），
∴关于x的方程ax2﹣bx﹣c＝0的解为x1＝﹣2，x2＝1，
故答案为：x1＝﹣2，x2＝1．
14．【解答】解：∵B（0，4），A（8，0），
∴OB＝4，OA＝8，
∵BM⊥CM，
∴∠BMC＝90°＝∠BOA＝90°，
（1）当M是OA的中点，如图所示，
∴，
∴OM＝OB＝4，
∴△BOM是等腰直角三角形，则∠OBM＝∠OMB＝45°，
∵∠BMO+∠CMB+∠CMA＝180°，
∴∠CMA＝180°﹣∠BMC﹣∠OMB＝180°﹣90°﹣45°＝45°，
∴∠BMO＝∠AMC＝45°，
∴，
在△ACM和△OBM中，
，
∴△ACM≌△OBM（SAS），
∴OB＝AC＝4；
故答案为：4；
（2）∵∠BOM＝∠BMC＝90°，
∴∠OMB+∠AMC＝∠OBM+∠OMB＝90°，
∴∠AMC＝∠OBM，
如图所示，作点B关于x轴的对称点B′，连接B′M，B′C，
∴BM＝B′M，
∵BM＝CM，
∴B′M＝MC，即△B′MC是等腰三角形，
∴点M在OA上运动时，△B′MC始终是等腰三角形，
∴点C在直线B′C上运动，
当AC⊥B′C时，AC的值最小，
如图所示，过点C作CD⊥x轴于点D，
在Rt△DMC和Rt△OBM中，
，
∴Rt△DMC≌Rt△OBM（AAS），
∴OM＝DC，OB＝DM＝4，
设M（m，0），则OM＝DC＝m，
∴C（m+4，m），点D（m+4，0），且B′（0，﹣4），
设直线B′C的解析式为y＝kx+b（k≠0），
∴，
解得，，
∴直线B′C的解析式为：y＝x﹣4，
设直线B′C与x轴交于点E，当y＝0时，x＝4，
∴E（4，0），
∴OE＝4，
∴AE＝OA﹣OE＝8﹣4＝4，
∵OB′＝OE＝4，∠B′OE＝90°，
∴∠OB′E＝∠OEB′＝45°＝∠CEA，且AC⊥B′C，
∴△ACE是等腰直角三角形，
∴EC＝AC，
在Rt△ACE中，AE2＝CE2+CA2＝2CA2，
∴，
∴AC的最小值为；
故答案为：．
三、（本大题共2小题，每小题0分，满分0分）
15．【解答】解：∵二次函数y＝x2+bx+c的图象经过点（﹣1，0），（1，﹣2），
∴，
解得：，
∴二次函数的解析式为y＝x2﹣x﹣2．
16．【解答】解：∵抛物线与直线y2＝x+6的图象交于A，B两点（点A在点B的左侧），
∴，
整理，得x2﹣2x﹣8＝0，
解得，或，
∴交点坐标为（﹣2，4），（4，10），
∵点A在点B的左侧，
∴点A的横坐标为﹣2，点B的横坐标为4．
四、（本大题共2小题，每小题8分，满分16分）
17．【解答】解：（1）因为y＝﹣3x2+6x+4＝﹣3（x﹣1）2+7，
所以抛物线的开口向下，对称轴为直线x＝1，顶点坐标为（1，7）．
（2）因为抛物线的开口向下，且对称轴是直线x＝1，
所以当x＞1时，y随x的增大而减小，
当x＜1时，y随x的增大而增大．
18．【解答】解：设矩形菜园的面积为S，设BC＝x m，则，
∴，
∴当x＝50时，S最大，最大值为1250m2，
∴，
∴当长为50m，宽为25m时，矩形菜园的面积最大，最大值为1250m2．
五、（本大题共2小题，每小题10分，满分20分）
19．【解答】解：（1）∵二次函数y＝﹣x2+bx+c的图象的顶点为（2，3），
∴设该二次函数的顶点式为y＝﹣（x﹣2）2+3＝﹣x2+4x﹣1，
∴b＝4，c＝﹣1；
（2）当y＝﹣1时，﹣（x﹣2）2+3＝﹣1，
解得：x＝0或4，
∴由图可知，当y≤﹣1时，x≥4或x≤0．
20．【解答】解：（1）∵二次函数y＝﹣x2+2x﹣m的图象与x轴有两个不同的交点，
∴一元二次方程﹣x2+2x﹣m＝0有两个不相等的实数根，
∴Δ＞0，即22﹣4×（﹣1）×（﹣m）＞0，解得m＜1；
（2）二次函数y＝﹣x2+2x﹣m的图象与x轴的其中一个交点坐标为（﹣1，0），
∴﹣1﹣2﹣m＝0，解得m＝﹣3，
∴一元二次方程﹣x2+2x﹣m＝0为﹣x2+2x+3＝0，解得x＝﹣1或3．
六、（本题满分12分）
21．【解答】解：（1）∵OA＝4，OB＝6，
∴A（4，0），B（0，6），
设直线AB的解析式为y＝kx+b（k≠0），
把A（4，0），B（0，6）代入得，
解得，
∴直线AB的解析式为，
根据题意设，则点P到x轴的距离为，
∵S△OAP＝6，即，
∴，即，
解得p＝2，
∴P（2，3），
∴4a﹣1＝3，
解得a＝1；
（2）由（1）可得二次函数的解析式为y＝x2﹣1，
∴经过平移后的解析式为y＝（x﹣2）2﹣1﹣t，
∵平移后的图象经过点A（4，0），
∴（4﹣2）2﹣1﹣t＝0，
解得t＝3．
七、（本题满分12分）
22．【解答】解：（1）由题意得：﹣100x+4000≥3000，
∴x≤10．
∵当每日销售量不低于3000kg时，成本价格为5元/kg；在销售中销售单价不低于成本价格且不高于30元/kg．
∴5≤x≤10，
故答案为：5≤x≤10；
（2）由题意，当5≤x≤10时，w＝（x﹣5）（﹣100x+4000）﹣2000＝﹣100x2+4500x﹣22000；
∵﹣100x+4000＜3000，
∴x＞10．
当10＜x≤30时，w＝（x﹣6）（﹣100x+4000）﹣2000＝﹣100x2+4600x﹣26000；
综上所述，；
（3）由题意，①当5≤x≤10时，w＝﹣100x2+4500x﹣22000＝﹣100（x﹣22.5）2+28625，
∵﹣100＜0，
∴当x＜22.5时，w随x的增大而增大，
∴当x＝10时，w最大，最大值为﹣100×（10﹣22.5）2+28625＝13000（元）；
②当10＜x≤30时，w＝﹣100x2+4600x﹣26000＝﹣100（x﹣23）2+26900，
∴当x＝23时，w最大，最大值为26900元，
综上所述，当销售单价定为23元时，销售这种板栗日获利最大，最大利润为26900元．
八、（本题满分14分）
23．【解答】解：（1）抛物线y＝ax2+bx+5（a≠0）与x轴交于A（5，0），C（﹣1，0）两点，交y轴于点B．把A，C的坐标代入得：
，
解得，，
∴二次函数解析式为：y＝﹣x2+4x+5；
（2）点P是第一象限内抛物线上的一点，直线PD⊥x轴于点D，交直线AB于点E．由（1）可得二次函数解析式为y＝﹣x2+4x+5＝﹣（x﹣2）2+9，
∴令x＝0时，y＝5，则B（0，5），
设直线AB的解析式为y＝kx+m（k≠0），
∴，
解得，
∴直线AB的解析式为y＝﹣x+5，
①∵点P是第一象限内抛物线上点，
∴设P（p，﹣p2+4p+5）（0＜p＜5），
∵PD⊥x轴交直线AB与点E，
∴D（p，0），E（p，﹣p+5），
∴PE＝﹣p2+4p+5﹣（﹣p+5）＝﹣p2+5p，DE＝﹣p+5，
当PE＝DE时，﹣p2+5p＝﹣p+5，整理得p2﹣6p+5＝0，
∴（p﹣1）（p﹣5）＝0，
解得，p1＝1，p2＝5（不符合题意，舍去），
当p＝1时，﹣p+5＝﹣1+5＝4，则E（1，4）；
∴当PE＝DE时，点E的坐标为（1，4）；
②已知，
∵﹣1＜0，
∴当时，PE有最大值，且最大值为，
此时，
∴点P的坐标为．
x
﹣1
0
1
3
y
﹣1
3
5
3