




- 热点专题 5.1 解三角形十类题型汇总(讲与练)-2025年高考数学二轮热点题型专题突破(新高考专用) 试卷 0 次下载
- 热点专题 6.1 平面向量重难点题型【17类题型汇总】(讲与练)-2025年高考数学二轮热点题型专题突破(新高考专用) 试卷 0 次下载
- 重难点专题 1.1 函数的对称性与周期性问题【18类题型】(讲与练)-2025年高考数学二轮热点题型专题突破(新高考专用) 试卷 0 次下载
- 重难点专题 1.2 抽象函数的赋值计算与模型总结【15类题型】(讲与练)-2025年高考数学二轮热点题型专题突破(新高考专用) 试卷 0 次下载
- 重难点专题 2.1 函数与方程10类常考压轴小题(讲与练)-2025年高考数学二轮热点题型专题突破(新高考专用) 试卷 0 次下载
重难点专题 2.2 三次函数图像与性质【10类题型】(讲与练)-2025年高考数学二轮热点题型专题突破(新高考专用)
展开一、注意基础知识的整合、巩固。进一步夯实基础,提高解题的准确性和速度。
二、查漏补缺,保强攻弱。针对“一模”中的问题根据实际情况作出合理的安排。
三、提高运算能力,规范解答过程。运算技巧粗中有细,提高运算准确性和速度。
四、强化数学思维,构建知识体系。同学们在听课时注意把重点要放到理解老师对问题思路的分析以及解法的归纳总结,以便于同学们在刷题时做到思路清晰,迅速准确。
五、解题快慢结合,改错反思。审题制定解题方案要慢,不要急于解题,要适当地选择好的方案,一旦方法选定,解题动作要快要自信。
六、重视和加强选择题的训练和研究。对于选择题不但要答案正确,还要优化解题过程,提高速度。灵活运用特值法、排除法、数形结合法、估算法等。
专题2-2 三次函数图像与性质
模块一
总览
热点题型解读(目录)
TOC \ "1-3" \n \h \z \u \l "_Tc171962609" 【题型1】求三次函数的解析式
\l "_Tc171962610" 【题型2】三次函数的单调性问题
\l "_Tc171962611" 【题型3】三次函数的图像
\l "_Tc171962612" 【题型4】三次函数的最值、极值问题
\l "_Tc171962613" 【题型5】三次函数的零点问题
\l "_Tc171962614" 【题型6】三次函数图像,单调性,极值,最值综合问题
\l "_Tc171962615" 【题型7】 三次函数对称中心
\l "_Tc171962616" 【题型8】三次函数的切线问题
\l "_Tc171962617" 【题型9】三次函数根与系数的关系
模块二
核心题型·举一反三(讲与练)
【题型1】求三次函数的解析式
(1)一般式:(a≠0)
(2)交点式:(a≠0)
若三次函数满足,则( )
A.38B.171C.460D.965
【题型2】三次函数的单调性问题
三次函数是高中数学中的一个重要内容,其考点广泛且深入,主要涉及函数的性质、图像、最值、零点以及与其他函数的综合应用等方面。以下是对三次函数常见考点的详细分析:
1. 三次函数的定义与形式
定义:形如 f(x)=ax3+bx2+cx+d(其中 a≠=0)的函数称为三次函数。
形式:注意系数 a,b,c,d 的作用,特别是 a 的正负决定了函数的开口方向(a>0 开口向上,a<0 开口向下)。
2. 函数的单调性
导数应用:利用导数 f′(x)=3ax2+2bx+c 判断函数的单调性。解不等式 f′(x)>0 和 f′(x)<0 得到函数的单调递增和递减区间。
极值点:导数等于0的点(f′(x)=0)可能是极值点,需结合单调性判断是否为极大值或极小值点。
2024·广东茂名市·一模
(多选)若是区间上的单调函数,则实数的值可以是( )
A. B. C. 3D. 4
【巩固练习】三次函数在上是减函数,则的取值范围是( )
A.B.C.D.
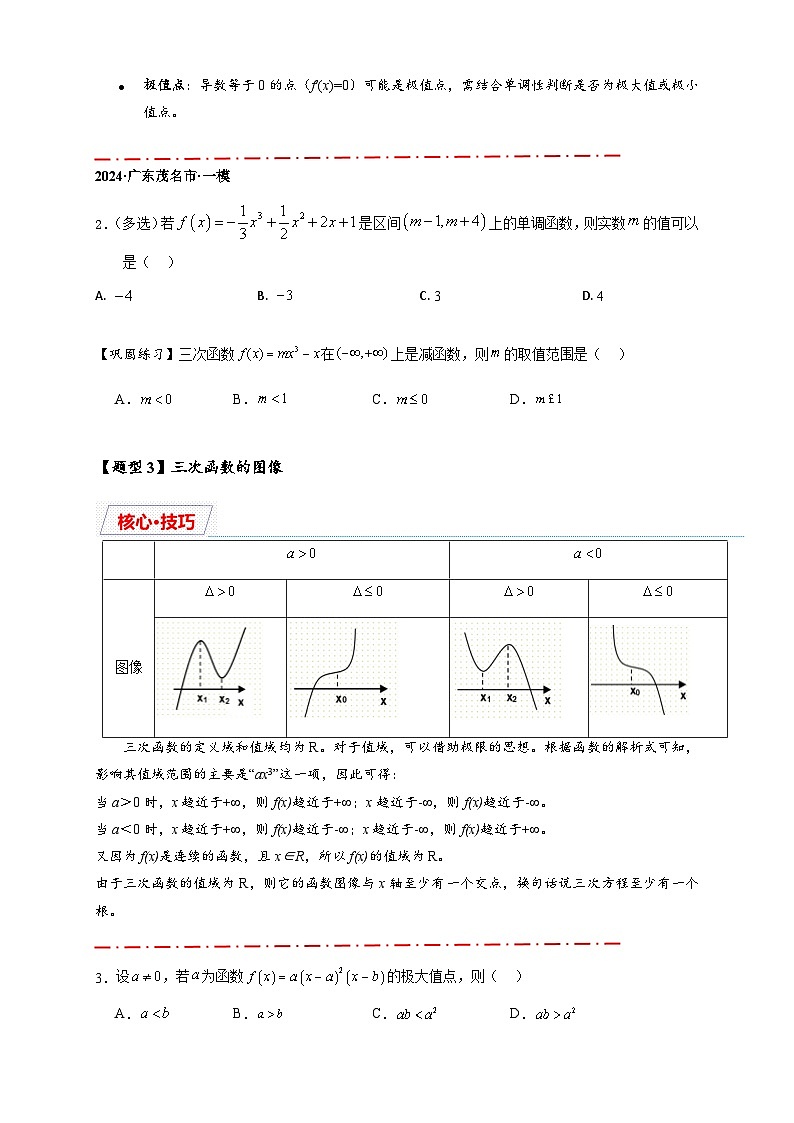
【题型3】三次函数的图像
三次函数的定义域和值域均为R。对于值域,可以借助极限的思想。根据函数的解析式可知,影响其值域范围的主要是“ax3”这一项,因此可得:
当a>0时,x趋近于+∞,则f(x)趋近于+∞;x趋近于-∞,则f(x)趋近于-∞。
当a<0时,x趋近于+∞,则f(x)趋近于-∞;x趋近于-∞,则f(x)趋近于+∞。
又因为f(x)是连续的函数,且x∈R,所以f(x)的值域为R。
由于三次函数的值域为R,则它的函数图像与x轴至少有一个交点,换句话说三次方程至少有一个根。
设,若为函数的极大值点,则( )
A.B.C.D.
(2024·全国一卷真题)(多选)设函数,则( )
A.是的极小值点B.当时,
C.当时,D.当时,
【巩固练习1】(多选题)(2024·湖北武汉·模拟预测)设函数,则下列结论正确的是( )
A.存在实数使得B.方程有唯一正实数解
C.方程有唯一负实数解D.有负实数解
【巩固练习2】(2024·全国甲卷(文)真题)曲线与在上有两个不同的交点,则的取值范围为 .
【题型4】三次函数的最值、极值问题
三次函数的极值与最值
极值:通过导数等于0找到可能的极值点,并判断其类型(极大值或极小值)。
最值:在闭区间上,最值可能出现在端点或极值点处。需比较这些点的函数值来确定全局最值。
已知三次函数无极值,且满足,则 .
已知三次函数f(x)=x3-(4m-1)x2+(15m2-2m-7)x+2在定义域R上无极值点,则m的取值范围是( )
A.m<2或m>4B.或
C.D.2<m<4
【巩固练习1】已知三次函数,其导函数为,存在,满足.记的极大值为,则的取值范围是 .
【巩固练习2】(2024·全国·模拟预测)已知三次函数的极小值点为,极大值点为,则等于( )
A.B.
C.D.
【题型5】三次函数的零点问题
三次方程的实根个数
设三次函数
其导函数为二次函数:,
判别式为:△=,设的两根为、,结合函数草图易得:
(1) 若,则恰有一个实根;
(2) 若,且,则恰有一个实根;
(3) 若,且,则有两个不相等的实根;
(4) 若,且,则有三个不相等的实根.
说明:(1)(2)含有一个实根的充要条件是曲线与轴只相交一次,即在R上为单调函数(或两极值同号),所以(或,且);
(5)有两个相异实根的充要条件是曲线与轴有两个公共点且其中之一为切点,所以,且;
(6)有三个不相等的实根的充要条件是曲线与轴有三个公共点,即有一个极大值,一个极小值,且两极值异号.所以且.
(2023·全国·高考真题)函数存在3个零点,则的取值范围是( )
A.B.C.D.
若要存在3个零点,则,即,解得
已知三次函数有三个零点,,,且在点处切线的斜率为,则 .
已知,,,若三次函数有三个零点,,,且满足,,则的取值范围是( )
A.B.C.D.
【巩固练习1】已知三次函数的零点从小到大依次为m,0,2,其图象在处的切线l经过点,则( )
A.B.C.D.
【巩固练习2】(2024·全国·一模)已知三次函数,,且有三个零点.若三次函数和均为上的单调函数,且这两个函数的导函数均有零点,则零点的个数为( )
A.个B.个C.个D.个或个
【巩固练习3】已知,为三次函数,其图象如图所示.若有9个零点,则的取值范围是 .
【巩固练习4】已知三次函数有两个零点,若方程有四个实数根,则实数a的范围为( )
A.B.C.D.
【题型6】三次函数图像,单调性,极值,最值综合问题
(24-25高三上·云南·阶段练习)(多选)已知函数,则( )
A.有两个极值点
B.点是曲线的对称中心
C.有三个零点
D.直线是曲线的一条切线
(多选题)(2024·全国·模拟预测)已知函数下列结论中正确的是( )
A.若,则是的极值点
B.,使得
C.若是的极小值点,则在区间上单调递减
D.函数的图象是中心对称图形
【巩固练习1】函数的图像如图所示,则的取值范围是 .
【巩固练习2】(23-24高三·广东清远·期末)(多选)已知函数,则下列选项中正确的是( )
A.的值域为
B.在处取得极小值为2
C.在上是增函数
D.若方程有2个不同的根,则
【巩固练习3】2024·金华联考模拟(多选题)已知函数,则()
A.函数在区间上单调递减
B.函数在区间上的最大值为1
C.函数在点处的切线方程为
D.若关于的方程在区间上有两解,则
【题型7】 三次函数对称中心
二阶导数的零点即为对称中心横坐标,即则为函数的对称中心
设三次函数,则对称中心是;
三次函数f(x)的对称中心为,则
已知三次函数的极小值点为,极大值点为,则等于( )
A.B.
C.D.
人们在研究学习过程中,发现:三次整式函数都有对称中心,其对称中心为(其中).已知函数.若,则( )
A.B.C.D.
已知一元三次函数对称中心的横坐标为其二阶导函数的零点.若,则( )
A.0B.4C.D.
(2024·全国2卷·高考真题)(多选)设函数,则( )
A.当时,有三个零点
B.当时,是的极大值点
C.存在a,b,使得为曲线的对称轴
D.存在a,使得点为曲线的对称中心
对于三次函数,给出定义:是函数的导数,是函数的导数,若方程有实数解,则称为函数的“拐点”.某同学经探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.若函数,则下列说法正确的是( )
A.的极大值为
B.有且仅有2个零点
C.点是的对称中心
D.
【巩固练习1】已知三次函数,若,则 .
【巩固练习2】已知所有的三次函数的图象都有对称中心,,若函数,则 .
【巩固练习3】(2024·四川成都·模拟预测)(多选)已知函数,则( )
A.有两个极值点
B.有一个零点
C.点是曲线的对称中心
D.直线是曲线的切线
【巩固练习4】(多选题)(2024·江苏·模拟预测)已知三次函数,若函数的图象关于点(1,0)对称,且,则( )
A.B.有3个零点
C.的对称中心是D.
【题型8】三次函数的切线问题
一般地,过三次函数图象的对称中心作切线,则坐标平面被切线和函数的图象分割为四个区域,有以下结论:
(1)过区域内的点作的切线,有且仅有3条;
(2)过区域Ⅱ、Ⅲ内的点以及对称中心作的切线,有且仅有1条;
(3)过切线或函数图象(除去对称中心)上的点作的切线,有且仅有2条.
已知函数在点处的切线方程为.若经过点可以作出曲线的三条切线,则实数的取值范围为 .
(多选题)(2024·山西晋中·二模)对于三次函数,给出定义:设是函数的导数,是函数的导数,若方程有实数解,则称为函数的“拐点”.某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.若函数,则( )
A.一定有两个极值点
B.函数在R上单调递增
C.过点可以作曲线的2条切线
D.当时,
【巩固练习1】(2022·新高考一卷真题)(多选)已知函数,则( )
A.有两个极值点B.有三个零点
C.点是曲线的对称中心D.直线是曲线的切线
【巩固练习2】(多选题)(山东省枣庄市2024届高三第二次模拟考试数学试题)已知函数,则下列结论正确的是( )
A.当时,若有三个零点,则b的取值范围为
B.若满足,则
C.若过点可作出曲线的三条切线,则
D.若存在极值点,且,其中,则
【巩固练习3】(多选题)下列关于三次函数叙述正确的是( )
A.函数的图象一定是中心对称图形
B.函数可能只有一个极值点
C.当时,在处的切线与函数的图象有且仅有两个交点
D.当时,则过点的切线可能有一条或者三条
【题型9】三次函数根与系数的关系
三次函数根与系数关系:对于,若有3个交点,则
方程可以写为,
展开后得
比对系数,则有:,,,
2024届·广东省“六校”高三上学期9月联合摸底
(多选)已知三次函数有三个不同的零点,若函数也有三个不同的零点,则下列等式或不等式一定成立的有( )
A.B.
C.D.
(2024·衢州、丽水、湖州·统考一模)(多选)已知函数,若,其中,则( )
A.B.C.D.
【巩固练习1】(2023届·深圳一模)(多选)已知函数,若,其中,则( )
A.B.
C.D.的取值范围为
【巩固练习2】(2024·重庆育才中学·阶段练习)(多选)已知三次函数有三个不同的零点,函数.则( )
A.
B.若成等差数列,则
C.若恰有两个不同的零点,则
D.若有三个不同的零点,则
近5年考情(2020-2024)
考题统计
考点分析
考点要求
2024年甲卷(文),第16题,5分
考查频率:三次函数图像与性质的考查在近五年高考中保持一定频率,尤其在新课标全国卷中较为常见。
考点内容:主要考查三次函数的图像特征(如中心对称性、开口方向)、单调性(通过导数分析)、极值点(一阶导数为零的点)以及图像与性质的综合应用。
题型分布:常以选择题、填空题或解答题的形式出现,涉及三次函数的零点、最值、极值、单调区间等具体问题。
难度变化:随着高考改革的深入,对三次函数图像与性质的考查更加注重学生的综合分析能力和解题技巧,难度可能略有提升。
备考建议:考生应熟练掌握三次函数的基本性质,灵活运用导数工具进行分析,同时注重题目类型的多样性和综合应用能力的培养。
(1)理解三次函数的定义域、值域和图像特点。
(2)掌握三次函数的导数与单调性关系。
(3)判断三次函数的极值点及其个数。
(4)探究三次函数图像与x轴的交点个数。
(5)熟练运用三次函数的对称中心性质。
2024年新高考I卷,第10题,6分
2024年新高考II卷,第11题,6分
2022年新高考I卷,第10题,5分
图像
图像
重难点专题 1.2 抽象函数的赋值计算与模型总结【15类题型】(讲与练)-2025年高考数学二轮热点题型专题突破(新高考专用): 这是一份重难点专题 1.2 抽象函数的赋值计算与模型总结【15类题型】(讲与练)-2025年高考数学二轮热点题型专题突破(新高考专用),文件包含重难点专题12抽象函数的赋值计算与模型总结15类题型原卷版docx、重难点专题12抽象函数的赋值计算与模型总结15类题型解析版docx等2份试卷配套教学资源,其中试卷共56页, 欢迎下载使用。
重难点专题 1.1 函数的对称性与周期性问题【18类题型】(讲与练)-2025年高考数学二轮热点题型专题突破(新高考专用): 这是一份重难点专题 1.1 函数的对称性与周期性问题【18类题型】(讲与练)-2025年高考数学二轮热点题型专题突破(新高考专用),文件包含重难点专题11函数的对称性与周期性问题18类题型原卷版docx、重难点专题11函数的对称性与周期性问题18类题型解析版docx等2份试卷配套教学资源,其中试卷共106页, 欢迎下载使用。
热点专题 6.1 平面向量重难点题型【17类题型汇总】(讲与练)-2025年高考数学二轮热点题型专题突破(新高考专用): 这是一份热点专题 6.1 平面向量重难点题型【17类题型汇总】(讲与练)-2025年高考数学二轮热点题型专题突破(新高考专用),文件包含热点专题61平面向量重难点题型17类题型汇总原卷版docx、热点专题61平面向量重难点题型17类题型汇总解析版docx等2份试卷配套教学资源,其中试卷共142页, 欢迎下载使用。












