天津市重点中学2024年九上数学开学质量检测试题【含答案】

这是一份天津市重点中学2024年九上数学开学质量检测试题【含答案】，共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）已知点P（a，m），Q（b，n）是反比例函数y图象上两个不同的点，则下列说法不正确的是（ ）
A．am=2B．若a+b=0，则m+n=0
C．若b=3a，则nmD．若a＜b，则m＞n
2、（4分）如图，正方形ABCD中，AE垂直于BE，且AE＝3，BE＝4，则阴影部分的面积是（ ）
A．16B．18C．19D．21
3、（4分）10个人围成一圈做游戏.游戏的规则是：每个人心里都想一个数，并把目己想的数告诉与他相邻的两个人，然后每个人将与他相邻的两个人告诉他的数的平均数报出来，若报出来的数如图所示，则报出来的数是3的人心里想的数是（ ）
A．2B．C．4D．
4、（4分）如图：在菱形ABCD中，AC=6，BD=8，则菱形的边长为（ ）
A．5B．10C．6D．8
5、（4分）下列给出的条件中不能判定一个四边形是矩形的是( )
A．一组对边平行且相等，一个角是直角
B．对角线互相平分且相等
C．有三个角是直角
D．一组对边平行，另一组对边相等，且对角线相等
6、（4分）已知,,且,若,，则的长为（ ）
A．4B．9C．D．
7、（4分）如图，在菱形ABCD中，∠A＝110°，E，F分别是边AB和BC的中点，EP⊥CD于点P，则∠FPC＝（ ）
A．35°B．45°C．50°D．55°
8、（4分）小亮从家步行到公交车站台，等公交车去学校. 图中的折线表示小亮的行程s(km)与所花时间t(min)之间的函数关系. 下列说法错误的是
A．他离家8km共用了30minB．他等公交车时间为6min
C．他步行的速度是100m/minD．公交车的速度是350m/min
二、填空题（本大题共5个小题，每小题4分，共20分）
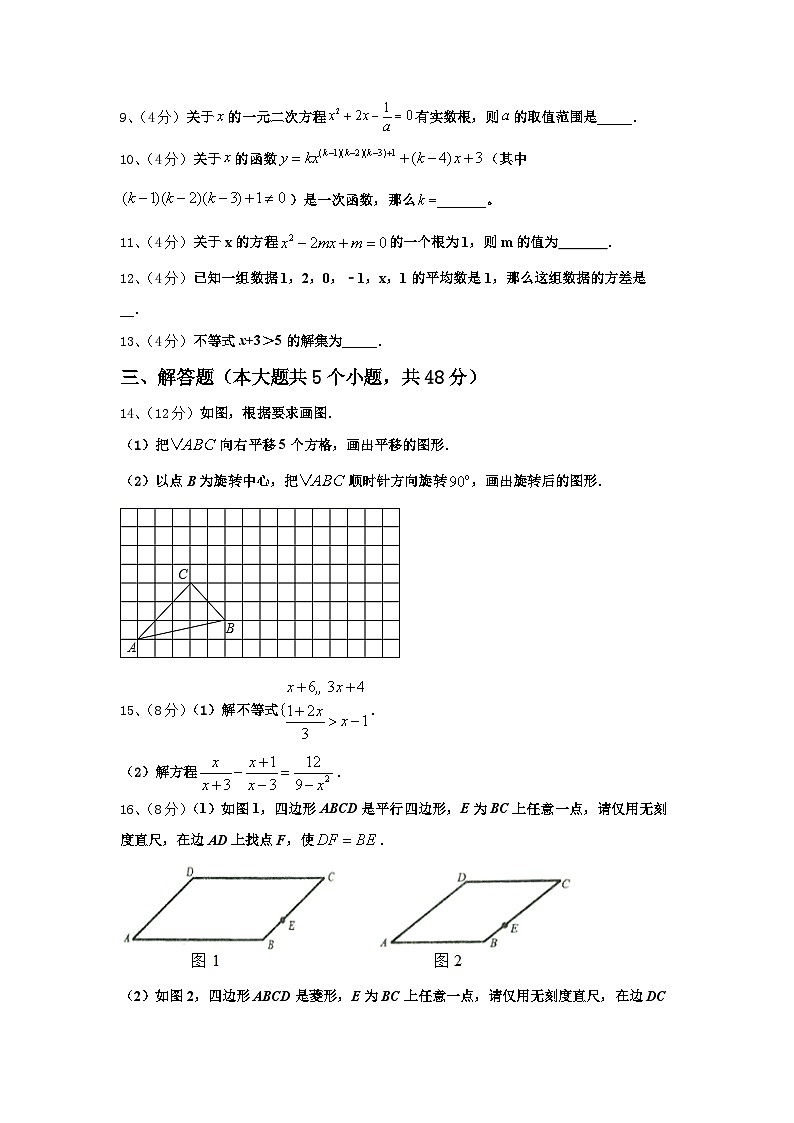
9、（4分）关于的一元二次方程有实数根，则的取值范围是_____．
10、（4分）关于的函数（其中）是一次函数，那么=_______。
11、（4分）关于x的方程的一个根为1，则m的值为 ．
12、（4分）已知一组数据1，2，0，﹣1，x，1的平均数是1，那么这组数据的方差是__．
13、（4分）不等式x+3＞5的解集为_____．
三、解答题（本大题共5个小题，共48分）
14、（12分）如图，根据要求画图．
（1）把向右平移5个方格，画出平移的图形．
（2）以点B为旋转中心，把顺时针方向旋转，画出旋转后的图形．
15、（8分）（1）解不等式．
（2）解方程．
16、（8分）（1）如图1，四边形ABCD是平行四边形，E为BC上任意一点，请仅用无刻度直尺，在边AD上找点F，使．
（2）如图2，四边形ABCD是菱形，E为BC上任意一点，请仅用无刻度直尺，在边DC上找点M，使．
17、（10分）将两块全等的三角板如图①摆放，其中∠A1CB1=∠ACB=90°，∠A1=∠A=30°．
（1）将图①中的△A1B1C顺时针旋转45°得图②，点P1是A1C与AB的交点，点Q是A1B1与BC的交点，求证：CP1=CQ；
（2）在图②中，若AP1=2，则CQ等于多少？
18、（10分）一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图所示,结合图象回答下列问题.
(1)农民自带的零钱是多少?
(2) 由表达式你能求出降价前每千克的土豆价格是多少?试求降价前y与x之间的关系式
(3) 降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）某班同学要测量学校升国旗的旗杆高度，在同一时刻，量得某同学的身高是1.5米，影长是1米，且旗杆的影长为8米，则旗杆的高度是 _________________ 米.
20、（4分）如图，在Rt△ABC中，AC＝8，BC＝6，直线l经过点C，且l∥AB，P为l上一个动点，若△ABC与△PAC相似，则PC＝ .
21、（4分）李老师开车从甲地到相距240千米的乙地,如果油箱剩余油量y（升）与行驶里程x（千米）之间是一次函数关系,其图象如图所示,那么到达乙地时油箱剩余油量是 升.
22、（4分）如图，在平面直角坐标系中，菱形的顶点在轴上，边在轴上，若点的坐标为，则点的坐标是____.
23、（4分）面试时，某人的基本知识、表达能力、工作态度的成绩分别是90分、80分、85分，若依次按20%、40%、40%的比例确定成绩，则这个人的面试成绩是_______.
二、解答题（本大题共3个小题，共30分）
24、（8分）如图，设线段AB的中点为C，以AC和CB为对角线作平行四边形AECD、又作平行四边形CFHD、CGKE．
求证：H，C，K三点共线．
25、（10分）贵成高铁开通后极大地方便了人们的出行，甲、乙两个城市相距450千米，加开高铁列车后，高铁列车行驶时间比原特快列车行驶时间缩短了3小时，已知高铁列车平均行驶速度是原特快列车平均行驶速度的3倍，求高铁列车的平均行驶速度．
26、（12分）计算:
(1); (2).
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、D
【解析】
根据题意得：am=bn=2，将B，C选项代入可判断，根据反比例函数图象的性质可直接判断D是错误的．
【详解】
∵点P(a，m)，Q(b，n)是反比例函数y图象上两个不同的点，
∴am=bn=2，
若a+b=0，则a=﹣b，
∴﹣bm=bn，
∴﹣m=n即m+n=0，
若b=3a，∴am=3an，
∴nm，
故A，B，C正确，
若a＜0＜b，则m＜0，n＞0，
∴m＜n，
故D是错误的，
故选D．
本题考查了反比例函数图象上点的坐标特征，关键是灵活运用反比例函数图象的性质解决问题．
2、C
【解析】
由已知得△ABE为直角三角形，用勾股定理求正方形的边长AB，用S阴影部分=S正方形ABCD-S△ABE求面积．
【详解】
∵AE⊥BE，且AE=3，BE=4，
∴在Rt△ABE中，AB3=AE3+BE3=35，
∴S阴影部分=S正方形ABCD﹣S△ABE=AB3﹣×AE×BE=35﹣×3×4=3．
故选C．
考点：3．勾股定理；3．正方形的性质．
3、B
【解析】
先设报3的人心里想的数为x，利用平均数定义表示报5的人心里想的数；报7的人心里想的数；报9的人心里想的数；报1的人心里想的数，最后建立方程，解方程即可.
【详解】
设报3的人心里想的数是x
∵报3与报5的两个人报的数的平均数是4
∴报5的人心里想的数应该是8-x
于是报7的人心里想的数应该是12-（8-x）=4+x
报9的人心里想的数应该是16-（4+x）=12-x
报1的人心里想的数应该是20-（12-x）=8+x
报3的人心里想的数应该是4-（8+x）=-4-x
所以x=-4-x，解得x=-2
故答案选择B.
本题属于阅读理解和探查规律题，考查的知识点有平均数的相关计算及方程思想的运用.规律与趋势：这道题的解决方法有点奥数题的思维，题意理解起来比较容易，但从哪下手却不容易想到，一般地，当数字比较多时，方程是首选的方法，而且，多设几个未知数，把题中的等量关系全部展示出来，再结合题意进行整合，问题即可解决.
4、A
【解析】
试题分析：根据菱形的性质：菱形的对角线互相垂直平分，且每一条对角线平分一组对角，可知每个直角三角形的直角边，根据勾股定理可将菱形的边长求出．
解：设AC与BD相交于点O，
由菱形的性质知：AC⊥BD，OA=AC=3，OB=BD=4
在Rt△OAB中，AB===1
所以菱形的边长为1．
故选A．
考点：菱形的性质．
5、D
【解析】
利用矩形的判定定理：①有三个角是直角的四边形是矩形可对C作出判断；根据一组对边平行且相等的四边形是平行四边形及有一个角是直角的平行四边形是矩形，可对A作出判断；利用对角线互相平分的四边形是平行四边形，及对角线相等的平行四边形是矩形，可对B作出判断；即可得出答案.
【详解】
解：A.∵ 一组对边平行且相等的四边形是平行四边形，且此四边形有一个角是直角，
∴此四边形是矩形，故A不符合题意；
B、∵对角线互相平分的四边形是平行四边形，
∵此四边形的对角线相等，
∴此四边形是矩形，故B不符合题意；
C、有三个角是直角的四边形是矩形，故C不符合题意；
D、一组对边平行，另一组对边相等，且对角线相等的四边形可能是等腰梯形，故D符合题意；
故答案为：D
此题考查了矩形的判定，矩形的判定方法有：有一个角是直角的平行四边形是矩形；三个角都是直角的四边形是矩形；对角线相等的平行四边形是矩形，熟练掌握矩形的判定方法是解本题的关键．
6、B
【解析】
根据勾股定理求出两点间的距离，进而得，然后代入CD=即可求出CD.
【详解】
解：∵，，且，
∴AB=，
则，
又∵，，
CD=
=
=
=9，
故选：B.
本题考查的是用勾股定理求两点间的距离，求出是解题的关键．
7、D
【解析】
延长PF交AB的延长线于点G．根据已知可得∠B，∠BEF，∠BFE的度数，再根据余角的性质可得到∠EPF的度数，从而不难求得∠FPC的度数．
【详解】
解：延长PF交AB的延长线于点G．
在△BGF与△CPF中，

∴△BGF≌△CPF（ASA），
∴GF＝PF，
∴F为PG中点．
又∵由题可知，∠BEP＝90°，
∴（直角三角形斜边上的中线等于斜边的一半），
∵（中点定义），
∴EF＝PF，
∴∠FEP＝∠EPF，
∵∠BEP＝∠EPC＝90°，
∴∠BEP﹣∠FEP＝∠EPC﹣∠EPF，即∠BEF＝∠FPC，
∵四边形ABCD为菱形，
∴AB＝BC，∠ABC＝180°﹣∠A＝70°，
∵E，F分别为AB，BC的中点，
∴BE＝BF，
易证FE＝FG，
∴∠FGE＝∠FEG＝55°，
∵AG∥CD，
∴∠FPC＝∠EGF＝55°
故选：D．
此题主要考查了菱形的性质的理解及运用，灵活应用菱形的性质是解决问题的关键．
8、D
【解析】
A、依题意得他离家8km共用了30min，故选项正确；
B、依题意在第10min开始等公交车，第16min结束，故他等公交车时间为6min，故选项正确；
C、他步行10min走了1000m，故他步行的速度为他步行的速度是100m/min，故选项正确；
D、公交车（30-16）min走了（8-1）km，故公交车的速度为7000÷14=500m/min，故选项错误．
故选D．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、或
【解析】
根据一元二次方程根的判别式与根的情况的关系，求解判别式中的未知数.
【详解】
一元二次方程中，叫做一元二次方程的根的判别式，通常用“”来表示，即，当 时，方程有2个实数根，当时，方程有1个实数根（2个相等的实数根），当 时，方程没有实数根.
一元二次方程有实数根，则，可求得或.
本题考查根据一元二次方程根的判别式.
10、、、
【解析】
根据一次函数的定义解答．
【详解】
依题意得：（k-1）（k-2）（k-2）+1=1或k=1，
所以（k-1）（k-2）（k-2）=1或k=1，
当k=2时，不是一次函数，
故k≠2，
所以，k-1=1或k-2=1或k=1，
所以k=1或k=2或k=1．
故答案是：1或1或2．
考查了一次函数的定义，一般地，形如y=kx+b（k≠1，k、b是常数）的函数，叫做一次函数．
11、1
【解析】
试题分析：把x=1代入方程得：1-2m+m=0，解得m=1.
考点：一元二次方程的根.
12、
【解析】
先由平均数的公式计算出x的值，再根据方差的公式计算．一般地设n个数据，x1，x2，…xn的平均数为Z，则方差S2＝ [（x1﹣）2+（x2﹣）2+…+（xn﹣）2]．
【详解】
x＝1×6﹣1﹣2﹣0﹣（﹣1）﹣1＝3
s2＝ [（1﹣1）2+（2﹣1）2+（0﹣1）2+（﹣1﹣1）2+（3﹣1）2+（1﹣1）2]＝．
故答案为．
本题考查了方差的定义：一般地设n个数据，x1，x2，…xn的平均数为，则方差S2＝ [（x1﹣）2+（x2﹣）2+…+（xn﹣）2]，它反映了一组数据的波动大小，方差越大，波动性越大，反之也成立．
13、x＞1．
【解析】
利用不等式的基本性质，把不等号左边的3移到右边，合并同类项即可求得原不等式的解集．
【详解】
移项得，x＞5﹣3，
合并同类项得，x＞1．
故答案为：x＞1．
本题主要考查了一元一次不等式的解法，解不等式要依据不等式的基本性质．
三、解答题（本大题共5个小题，共48分）
14、（1）答案见解析；（2）答案见解析．
【解析】
（1）分别作出点A、B、C向右平移5个方格所得对应点，再顺次连接可得；
（2）分别作出点A、C绕点B顺时针方向旋转所得对应点，再顺次连接可得．
【详解】
解：如图所示，（1）即为平移后的图形；
（2）即为旋转后的图形．
本题主要考查作图旋转变换、平移变换，解题的关键是根据旋转变换和平移变换的定义作出变换后的对应点．
15、
【解析】
（1）分别求出不等式组中两不等式的解集，找出两解集的公共部分即可；
（2）分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．
【详解】
（1），
由①得：，
由②得：，
则不等式组的解集为；
（2）去分母得：，
解得：，
经检验是分式方程的解.
此题考查了解分式方程，以及解一元一次不等式组，熟练掌握运算法则是解本题的关键．
16、（1）答案见解析；（2）答案见解析.
【解析】
（1）先连接AC、BD，再连接对角线交点O与E点与DA的交点F即为所求；
（2）连接AC，DE交于点O，再连接O点与B点交CD于M点，M点即为所求.
【详解】
解：（1）如下图，点F即为所求：
（2）如下图，点M即为所求：
本题考查的是无刻度尺规作图，主要用到的知识点为三角形全等的判定与性质.
17、（1）证明见解析；（2）CQ=
【解析】
分析：（1）利用△A1CB1≌△ACB得到CA1=CA，再根据旋转的性质得∠B1CB=∠A1CA=45°，则∠BCA1=45°，于是根据“ASA”判断△CQA1≌△CP1A，所以CP1=CQ；
（2）过点P1作P1P⊥AC于点P，如图②，先在Rt△AP1P中根据含30度的直角三角形三边的关系得到P1P=AP1=×2=1，然后在Rt△CP1P中利用等腰直角三角形的性质得CP=P1P=1，CP1=PP1=，由（1）得CQ=CP1=．
详解：（1）∵△A1CB1≌△ACB，∴CA1=CA．
∵图①中的△A1B1C顺时针旋转45°得图②，∴∠B1CB=∠A1CA=45°，∴∠BCA1=45°．
在△CQA1和△CP1A中，∵，∴△CQA1≌△CP1A，∴CP1=CQ；
（2）过点P1作P1P⊥AC于点P，如图②．在Rt△AP1P中，∵∠A=30°，∴P1P=AP1=×2=1．在Rt△CP1P中，∵∠P1CP=45°，∴CP=P1P=1，∴CP1=PP1=，∴CQ=CP1=．
点睛：本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．旋转有三要素：旋转中心；旋转方向；旋转角度．也考查了等腰直角三角形的性质．
18、（1) 5元(2) 0.5元/千克； y=x+5（0≤x≤30）；（3）他一共带了45千克土豆.
【解析】
(1)根据题意得出自带的零钱；(2)根据图象可知降价前售出的土豆数量为30千克，总金额为15元，然后计算单价；根据降价后的价格和金额求出降价后售出的数量，然后计算总质量.
【详解】
(1)根据图示可得：农民自带的零钱是5元.
(2)(20－5)÷30=0.5(元/千克) ∴y=x+5（0≤x≤30）
答：降价前他出售的土豆每千克是0.5元.
(3)(26－20)÷0.4+30=15+30=45(千克) 答：他一共带了45千克土豆.
考点：一次函数的应用.
一、填空题（本大题共5个小题，每小题4分，共20分）
19、1．
【解析】
在同一时刻，物体的实际高度和影长成比例，据此列方程即可解答．
【详解】
解：设旗杆高度为x，则
，
解得x=1．
故答案为：1．
本题考查相似三角形的应用，熟知同一时刻物高与影长成正比是解题关键．
20、6.1或2
【解析】
分类讨论：（1）当∠PCA=90°时，不成立；
（2）∵Rt△ABC中，AC＝8，BC＝6，∴AB=2，
当∠APC=90°时，
∵∠PCA=∠CAB,∠APC=∠ACB,
∴△CPA∽△ACB,
∴=,
∴=，
∴PC=6.1．
（3）当∠CAP=90°时，
∵∠ACB=∠CAP=90°，∠PCA=∠CAB，
∴△PCA∽△BAC，
∴=，
∴PC=AB=2．
故答案为：6.1或2．
点睛：（1）求相似三角形的第三个顶点时，先要分析已知三角形的边和角的特点，进而得出已知三角形是否为特殊三角形，根据未知三角形中已知边与已知三角形的可能对应分类讨论；
（2）或利用已知三角形中对应角，在未知三角形中利用勾股定理、三角函数、对称、旋转等知识来推导边的大小；
（3）若两个三角形的各边均未给出，则应先设所求点的坐标进而用函数解析式表示各边的长度，之后利用相似列方程求解．
21、1
【解析】
解：由图象可得出：行驶160km，耗油（35﹣25）=10（升），
∴行驶240km，耗油×10=15（升），
∴到达乙地时邮箱剩余油量是35﹣15=1（升）．
故答案为1．
22、C（0，-5）
【解析】
在Rt△ODC中，利用勾股定理求出OC即可解决问题
【详解】
解：∵A（12，13），
∴OD=12，AD=13，
∵四边形ABCD是菱形，
∴CD=AD=13，
在Rt△ODC中，，
∴C（0，-5）．
本题考查菱形的性质、勾股定理等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．
23、84分
【解析】
根据加权平均数的计算公式进行计算，即可得出答案．
【详解】
根据题意得：
90×20%+80×40%+85×40%=84(分)；
故答案为84分.
本题考查的是加权平均数，熟练掌握加权平均数的计算公式是解题的关键.
二、解答题（本大题共3个小题，共30分）
24、证明见解析.
【解析】
如图，连接DE交AC于N，连接EG交KC于M，连接DF交CH于Q，连接FG交BC于J，连接MN，NQ，QJ，JM，想办法证明四边形MNQJ是平行四边形即可解决问题；
【详解】
证明：如图，连接DE交AC于N，连接EG交KC于M，连接DF交CH于Q，连接FG交BC于J，连接MN，NQ，QJ，JM，DG．
四边形AECD是平行四边形，
，同法可证：，
，，
同法可证：，，
，，
四边形MNQJ是平行四边形，
与MQ互相平分，
，，，
、C、Q共线，
，C，K三点共线．
本题考查平行四边形的性质和判定，三角形中位线定理等知识，解题的关键是学会添加常用辅助线，构造特殊四边形解决问题．
25、高铁列车平均速度为300km/h．
【解析】
设原特快列车平均速度为xkm/h，则高铁列车平均速度为2.8xkm/h，利用高铁列车行驶时间比原特快列车行驶时间缩短了3小时，这一等量关系列出方程解题即可
【详解】
设原特快列车平均速度为xkm/h，则高铁列车平均速度为2.8xkm/h，
由题意得： +3＝，
解得：x＝100，
经检验：x＝100是原方程的解，
则3×100＝300（km/h）；
答：高铁列车平均速度为300km/h．
本题考查分式方程的简单应用，本题关键在于读懂题意列出方程，特别注意分式方程求解之后需要检验
26、（1）6（2）9
【解析】
（1）先计算算术平方根，零指数幂，然后依次计算即可
（2）先利用完全平方公式进行计算，再把二次根式化为最简，进行计算即可
【详解】
（1）3+2+1=6
（3）3+4+4 -4+2=9
此题考查二次根式的混合运算，掌握运算法则是解题关键
题号
一
二
三
四
五
总分
得分
批阅人