新疆吉木乃初级中学2024年数学九年级第一学期开学预测试题【含答案】

这是一份新疆吉木乃初级中学2024年数学九年级第一学期开学预测试题【含答案】，共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
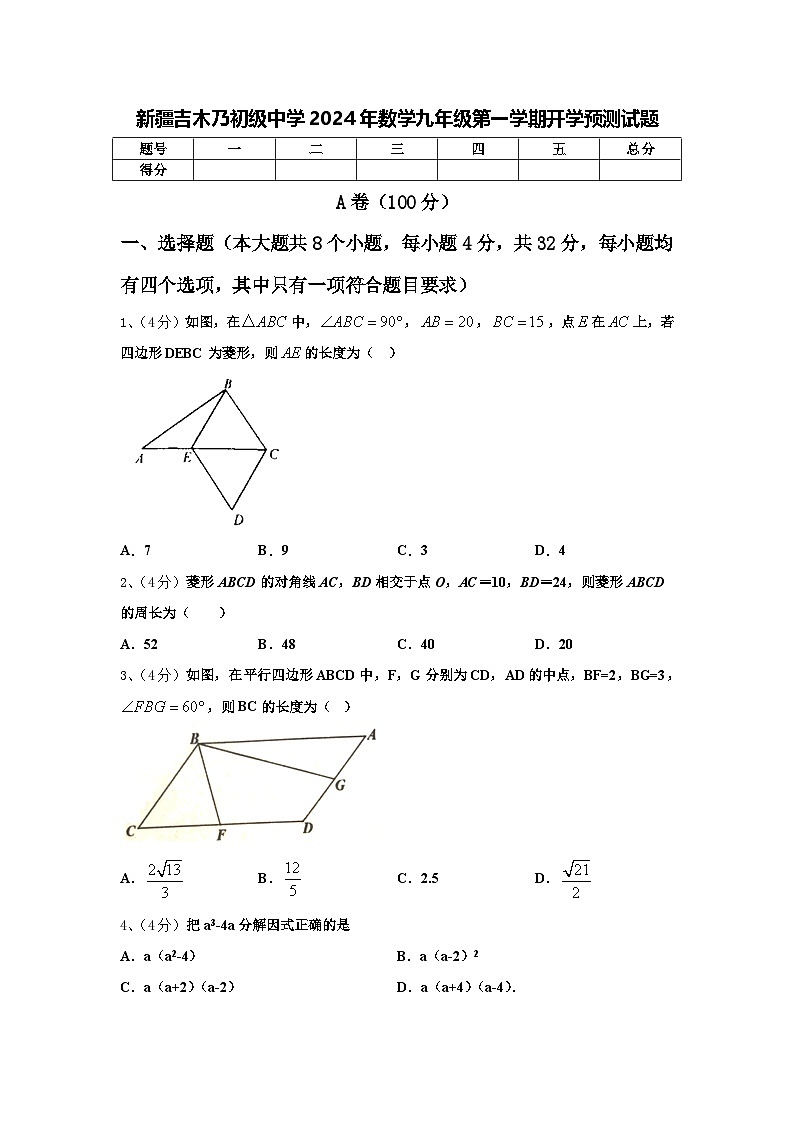
1、（4分）如图，在中，，，，点在上，若四边形DEBC为菱形，则的长度为（ ）
A．7B．9C．3D．4
2、（4分）菱形ABCD的对角线AC，BD相交于点O，AC＝10，BD＝24，则菱形ABCD的周长为（ ）
A．52B．48C．40D．20
3、（4分）如图，在平行四边形ABCD中，F，G分别为CD，AD的中点，BF=2，BG=3，，则BC的长度为（ ）
A．B．C．2.5D．
4、（4分）把a3-4a分解因式正确的是
A．a（a2-4）B．a（a-2）2
C．a（a+2）（a-2）D．a（a+4）（a-4）．
5、（4分）点A(1,-2)在正比例函数的图象上，则k的值是（ ）．
A．1B．-2C．D．
6、（4分）如图，在△ABC中，∠ACB=90°，分别以点A和点B为圆心以相同的长（大于AB）为半径作弧，两弧相交于点M和N点，作直线MN交AB于点D，交BC于点E，若AC=3，BC=4，则BE等于（ ）
A．B．C．D．
7、（4分）如图，等腰梯形 ABCD 的对角线 AC、BD 相交于 O，则图中的全等三 角形有（ ）
A．1 对B．2 对C．3 对D．4 对
8、（4分）将以此函数y=2x-1的图像向上平移2个单位长度后，得到的直线解析式为( )
A．y=2x+2B．y=2x+1C．y=2x+3D．y=2x-5
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图，为的中位线，点在上，且为直角，若 ，，则的长为_____．
10、（4分）在△ABC中，D，E分别为AC，BC的中点，若DE＝5，则AB＝_____．
11、（4分）如图，在△ABC中，AC＝BC＝9，∠C＝120°，D为AC边上一点，且AD＝6，E是AB边上一动点，连接DE，将线段DE绕点D逆时针旋转30°得到DF，若F恰好在BC边上，则AE的长为_____．
12、（4分）直角三角形的两边长为6cm,8cm，则它的第三边长是_____________。
13、（4分）将直线y＝2x+3向下平移2个单位，得直线_____．
三、解答题（本大题共5个小题，共48分）
14、（12分）八年级380名师生参加户外拓展活动,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表
(1)设租用乙种客车x辆,租车总费用为y元求出y(元)与x(辆)之间的函数表达式;
(2)当乙种客车租用多少辆时,能保障所有的师生能参加户外拓展活动且租车费用最少，最少费用是多少元?
15、（8分）（实践探究）
如图①，正方形的对角线相交于点，点又是正方形的一个顶点，而且这两个正方形的边长相等．无论正方形绕点怎样转动，两个正方形重叠部分的面积，总等于一个正方形面积的，你能说明这是为什么吗？
（拓展提升）
如图②，在四边形中，，，联结．若，求四边线的面积．
16、（8分）先化简，再求值：，其中x是不等式组的整数解．
17、（10分）2016年是中国工农红军长征胜利80周年，某商家用1200元购进了一批长征胜利主题纪念衫，上市后果然供不应求，商家又用2800元购进了第二批这种纪念衫，所购数量是第一批购进量的2倍，但单价贵了5元．
（1）该商家购进的第一批纪念衫单价是多少元？
（2）若两批纪念衫按相同的标价销售，最后剩下20件按标价八折优惠卖出，如果两批纪念衫全部售完利润不低于640元（不考虑其它因素），那么每件纪念衫的标价至少是多少元？
18、（10分）某地2015年为做好“精准扶贫”，投入资金1280万元用于异地安置，并规划投入资金逐年增加，2017年在2015年的基础上增加投入资金1600万元．
（1）从2015年到2017年，该地投入异地安置资金的年平均增长率为多少？
（2）在2017年异地安置的具体实施中，该地计划投入资金不低于500万元用于优先搬迁租房奖励，规定前1000户（含第1000户）每户每天奖励8元，1000户以后每户每天补助5元，按租房400天计算，试求今年该地至少有多少户享受到优先搬迁租房奖励？
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）如图，边长为4的菱形ABCD中，∠ABC＝30°，P为BC上方一点，且，则PB＋PC的最小值为___________．
20、（4分）如图，以的两条直角边分别向外作等腰直角三角形．若斜边，则图中阴影部分的面积为_____．
21、（4分）反比例函数y＝图象上有两个点（x1，y1），（x2，y2），其中0＜x1＜x2，则y1，y2的大小关系是_____（用“＜“连接）．
22、（4分）如图，在中，是的角平分线，，垂足为E，，则的周长为________．
23、（4分）小王参加某企业招聘测试，他的笔试、面试、技能操作得分分别为85分，80分，90分，若依次按照2：3：5的比例确定成绩，则小王的成绩________分．
二、解答题（本大题共3个小题，共30分）
24、（8分）某商店销售10台A型和20台B型电脑的利润为4000元，销售20台A型和10台B型电脑的利润为3500元．
（1）求每台A型电脑和B型电脑的销售利润；
（2）该商店计划一次购进两种型号的电脑共100台，其中B型电脑的进货量不超过A型电脑的2倍，设购进A型电脑x台，这100台电脑的销售总利润为y元．
①求y关于x的函数关系式；
②该商店购进A型、B型电脑各多少台，才能使销售总利润最大？最大利润是多少？
25、（10分）计算：
(1)；
(2)已知，，求的值.
26、（12分）计算
（1）分解因式：；
（2）解不等式组．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、A
【解析】
根据勾股定理得到AC==25， 连接BD交AC于O，由菱形的性质得到BD⊥CE，BO=DO，EO=CO，求得CE=2OE=18，于是得到结论．
【详解】
解：连接BD，交AC于点O，
在△ABC中，∠ABC=90°，AB=20，BC=15，
∴AC==25，
连接BD交AC于O，
∵四边形BCDE为菱形，
∴BD⊥CE，BO=DO，EO=CO，
∴BO===12，
∴OC==9，
∴CE=2OE=18，
∴AE=7，
故选：A．
本题考查菱形的性质，三角形的面积公式，勾股定理，正确的识别图形是解题的关键．
2、A
【解析】
由勾股定理可得AB的长，继而得到菱形ABCD的周长.
【详解】
因为菱形ABCD中，AC＝10，BD＝24，所以OB=12，OA=5.在直角三角形ABO中，AB=，所以菱形ABCD的周长=4AB=52，故答案为A.
本题考查勾股定理和菱形的性质，解题的关键是掌握勾股定理和菱形的性质.
3、A
【解析】
延长AD、BF交于E,过点E作EM⊥BG，根据F是中点得到△CBF≌△DEF，得到BE=2BF=4，根据得到BM=BE=2，ME=2，故MG=1，再根据勾股定理求出EG的长，再得到DE的长即可求解.
【详解】
延长AD、BF交于E,
∵F是中点，∴CF=DF,又AD∥BC，∴∠CBF=∠DEF，又∠CFB=∠DFE，
∴△CBF≌△DEF，∴BE=2BF=4，
过点E作EM⊥BG，∵，∴∠BEM=30°，
∴BM=BE=2，ME=2，
∴MG=BG-BM=1，
在Rt△EMG中，EG==
∵G为AD中点，∴DG=AD=DE，
∴DE==，
故BC=，
故选A.
此题主要考查平行四边形的线段求解，解题的关键是熟知全等三角形的判定及勾股定理的运用.
4、C
【解析】
先提取公因式a，再对余下的多项式利用平方差公式继续分解．
【详解】
a3-4a
=a（a2-4）
=a（a+2）（a-2）．
故选C．
提公因式法与公式法的综合运用．
5、B
【解析】
直接把点（1，-2）代入正比例函数y=kx（k≠0），求出k的值即可．
【详解】
∵正比例函数y=kx（k≠0）的图象经过点（1，-2），
∴-2=k．
故选B．
本题考查了一次函数图象上点的坐标特点，熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．
6、D
【解析】
连接AE，根据勾股定理求出AB，根据线段垂直平分线的性质得到AE=BE，根据勾股定理求出AE即可．
【详解】
解：连接AE，
∵∠ACB=90°，∴AB==5，
由题意得：MN是线段AB的垂直平分线，∴AE=BE，
在Rt△ACE中，AE2=AC2+CE2，即AE2=32+（4﹣AE）2，
解得：AE=，∴BE=AE=．
故选D．
本题考查的是线段的垂直平分线的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．
7、C
【解析】
由等腰梯形的性质可知，AB=CD，AC=BD，OA=OD，OB=OC，利用这些条件，就可以找图中的全等三角形了，有三对．
【详解】
∵四边形ABCD是等腰梯形，
∴AB=CD,AC=BD,OA=OD,OB=OC,AD∥CB，
∴△AOB≌△DOC,△ABD≌△ACD,△ABC≌△DCB.
故选C.
本题考查等腰梯形的性质, 全等三角形的判定.解本题时应先观察图，尽可能多的先找出图中的全等三角形，然后根据已知条件进行证明.
8、B
【解析】
直接根据一次函数图象与几何变换的有关结论求解．
【详解】
解：直线y=2x-1向上平移2个单位后得到的直线解析式为y=2x-1+2,即y=2x+1,
故选B．
本题考查了一次函数图象与几何变换：一次函数y=kx+b（k、b为常数，k≠0）的图象为直线，当直线平移时k不变，当向上平移m个单位，则平移后直线的解析式为y=kx+b+m．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、1cm．
【解析】
根据三角形中位线定理求出DE，根据直角三角形的性质求出EF，结合图形计算即可．
【详解】
∵DE为△ABC的中位线，
∴DE＝BC＝4（cm），
∵∠AFC为直角，E为AC的中点，
∴FE＝AC＝3（cm），
∴DF＝DE﹣FE＝1（cm），
故答案为1cm．
本题考查的是三角形中位线定理，直角三角形的性质，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键．
10、1．
【解析】
根据三角形中位线定理解答即可．
【详解】
∵D，E分别为AC，BC的中点，
∴AB＝2DE＝1，
故答案为：1．
本题考查的是三角形中位线定理，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键．
11、3+
【解析】
由，可知，又有，联想一线三等角模型，延长到，使，得，进而可得，，由于，即可得是直角三角形，易求，由即可解题．
【详解】
解：如图，延长到，使，连接，
，，
，，
，
又，
，
在和中，
，
，，
，
，
设，则，由得：
，
解得，（不合题意舍去），
，
，
故答案为：．
本题考查了旋转的性质：旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转中心的连线段的夹角等于旋转角．也考查了全等三角形的判定与性质和等腰直角三角形的性质．本题解题关键是通过一线三等角模型构造全等三角形，从而得到．
12、10cm或cm.
【解析】
分8cm的边为直角边与斜边两种情况，利用勾股定理进行求解即可.
【详解】
解：当8cm的边为直角边时，
第三边长为=10cm；
当8cm的边为斜边时，
第三边长为cm.
故答案为：10cm或cm.
本题主要考查勾股定理，解此题的关键在于分情况讨论.
13、y=2x+1．
【解析】
根据“左加右减，上加下减”的平移规律可得：将直线y=-2x+3先向下平移3个单位，得到直线y=－2x+3-2，即y=-2x+1.
故答案是：y=﹣2x+1.
三、解答题（本大题共5个小题，共48分）
14、（1）y=-100x+3850；（2）当乙为2辆时，能保障费用最少，最少费用为3650元.
【解析】
(1)y=租甲种车的费用+租乙种车的费用，由题意代入相关数据即可得；
(2)根据题意确定出x的取值范围，再根据一次函数的增减性即可得.
【详解】
(1)由题意，得
y=550(7-x)+450x，
化简，得y=-100x+3850，
即y(元)与x(辆)之间的函数表达式是y=-100x+3850；
(2)由题意，得45x+60(7﹣x)≥380，解得，x≤(x为自然数)，
∵y=-100x+3850中k=-100