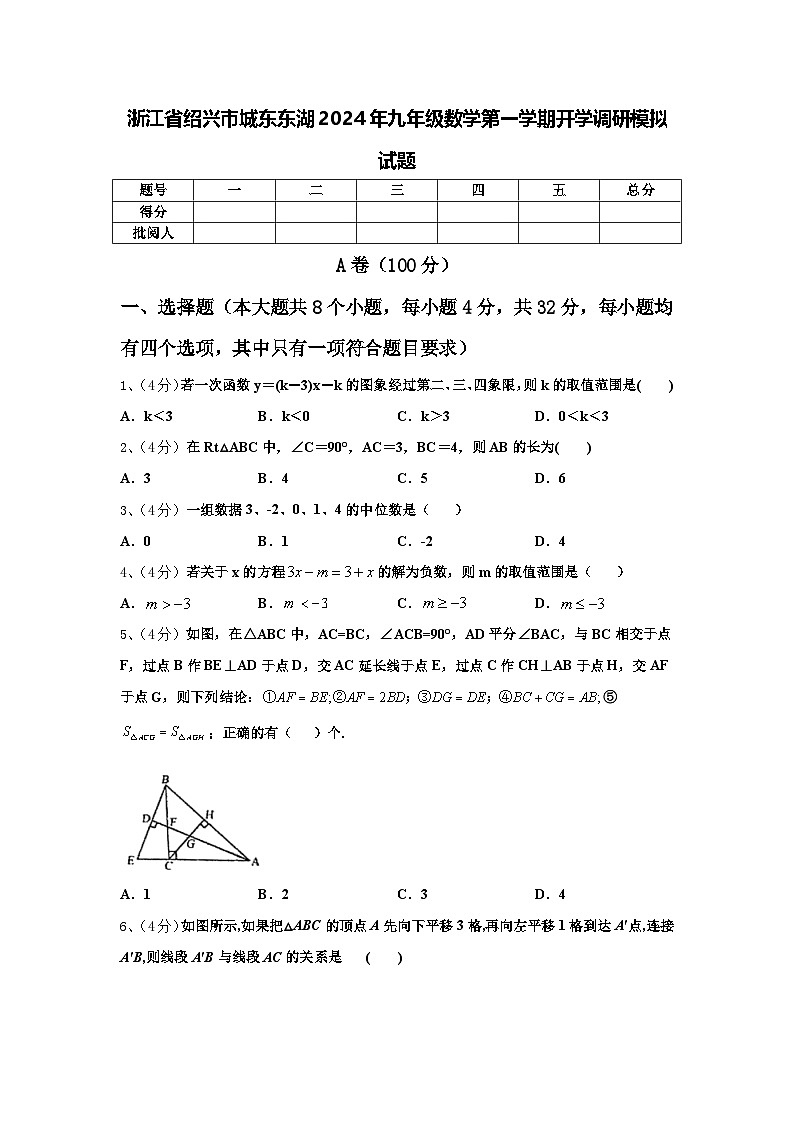
浙江省绍兴市城东东湖2024年九年级数学第一学期开学调研模拟试题【含答案】

这是一份浙江省绍兴市城东东湖2024年九年级数学第一学期开学调研模拟试题【含答案】，共24页。试卷主要包含了选择题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）若一次函数y＝(k－3)x－k的图象经过第二、三、四象限，则k的取值范围是( )
A．k＜3B．k＜0C．k＞3D．0＜k＜3
2、（4分）在Rt△ABC中，∠C＝90°，AC＝3，BC＝4，则AB的长为( )
A．3B．4C．5D．6
3、（4分）一组数据3、-2、0、1、4的中位数是（ ）
A．0B．1C．-2D．4
4、（4分）若关于x的方程的解为负数，则m的取值范围是（ ）
A．B．C．D．
5、（4分）如图，在△ABC中，AC=BC，∠ACB=90°，AD平分∠BAC，与BC相交于点F，过点B作BE⊥AD于点D，交AC延长线于点E，过点C作CH⊥AB于点H，交AF于点G，则下列结论：⑤；正确的有（ ）个.
A．1B．2C．3D．4
6、（4分）如图所示,如果把△ABC的顶点A先向下平移3格,再向左平移1格到达A'点,连接A'B,则线段A'B与线段AC的关系是 ( )
A．垂直B．相等C．平分D．平分且垂直
7、（4分）下列成语描述的事件为随机事件的是（ ）
A．水涨船高 B．守株待兔 C．水中捞月 D．缘木求鱼
8、（4分）多项式与多项式的公因式是（ ）
A．B．C．D．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图，两张等宽的纸条交叉叠放在一起，若重合部分构成的四边形中，，，则的长为_______________．
10、（4分）Rt△ABC与直线l：y＝﹣x﹣3同在如图所示的直角坐标系中，∠ABC＝90°，AC＝2，A（1，0），B（3，0），将△ABC沿x轴向左平移，当点C落在直线l上时，线段AC扫过的面积等于_____．
11、（4分）如图，线段AC、BD交于点O，请你添加一个条件：________，使△AOB∽△COD．
12、（4分）在中，，有一个锐角为，.若点在直线上（不与点、重合），且，则的长是___________
13、（4分）一个多边形的各内角都等于，则这个多边形的边数为______.
三、解答题（本大题共5个小题，共48分）
14、（12分）如图，四边形ABCD, AB//DC, ∠B=55,∠1=85,∠2=40
(1)求∠D的度数：
(2)求证：四边形ABCD是平行四边形
15、（8分）如图，四边形ABCD为菱形，E为对角线AC上的一个动点，连结DE并延长交射线AB于点F，连结BE．
（1）求证：∠AFD=∠EBC；
（2）若∠DAB=90°，当△BEF为等腰三角形时，求∠EFB的度数．
16、（8分）如图，矩形ABCD中，对角线AC与BD相交于点O．
（1）写出与相反的向量______；
（2）填空：++=______；
（3）求作：+（保留作图痕迹，不要求写作法）．
17、（10分）如图，在边长为1的小正方形网格中，△AOB的顶点均在格点上，
(1)将△AOB向右平移4个单位长度得到△A1O1B1，请画出△A1O1B1；
(2)以点A为对称中心，请画出△ AOB关于点A成中心对称的△ A O2 B2，并写点B2的坐标；
(1)以原点O为旋转中心，请画出把△AOB按顺时针旋转90°的图形△A2 O B1．
18、（10分）端午节前夕，小东妈妈准备购买若干个粽子和咸鸭蛋（每个棕子的价格相同，每个咸鸭蛋的价格相同）．已知某超市粽子的价格比咸鸭蛋的价格贵1.8元，小东妈妈发现，花30元购买粽子的个数与花12元购买的咸鸭蛋个数相同．
（1）求该超市粽子与咸鸭蛋的价格各是多少元？
（2）小东妈妈计划购买粽子与咸鸭蛋共18个，她的一张购物卡上还有余额40元，若只用这张购物卡，她最多能购买粽子多少个？
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）如图，在中，，，，点，都在边上，的平分线垂直于，垂足为，的平分线垂直于，垂足为，则的长__________.
20、（4分）已知P1（x1,y1），P2（x2 ，y2）两点都在反比例函数的图象上，且x1< x2 < 0，则y1 ____ y2.（填“>”或“
【解析】
根据反比例函数的增减性，k=1>0，且自变量x＜0，图象位于第三象限，y随x的增大而减小，从而可得结论．
【详解】
在反比例函数y=中，k=1＞0，
∴该函数在x＜0内y随x的增大而减小．
∵x1＜x1＜0，
∴y1＞y1．
故答案为：＞．
本题考查了反比例函数的性质，解题的关键是得出反比例函数在x＜0内y随x的增大而减小．本题属于基础题，难度不大，解决该题型题目时，根据系数k的取值范围确定函数的图象增减性是关键．
21、1
【解析】
试题分析：根据喜爱新闻类电视节目的人数和所占的百分比，即可求出总人数；根据总人数和喜爱动画类电视节目所占的百分比，求出喜爱动画类电视节目的人数，进一步利用减法可求喜爱“体育”节目的人数．
5÷1%=50（人），
50×30%=15（人），
50﹣5﹣15﹣20=1（人）．
故答案为1．
考点：条形统计图；扇形统计图.
22、2
【解析】
先由含30°角的直角三角形的性质,得出BC,再由三角形的中位线定理得出DE即可.
【详解】
因为，△ABC中，∠C=90°，∠A=30°，
所以， ,
因为，DE是中位线，
所以，.
故答案为2
本题考核知识点：直角三角形，三角形中位线. 解题关键点：熟记直角三角形性质，三角形中位线性质.
23、
【解析】
求概率时，已知和未知与几何有关的就是几何概率．计算方法是长度比，面积比，体积比等．
【详解】
设最小正方形的边长为1，则小正方形边长为2，
阴影部分面积=2×2×4+1×1×2=18，
白色部分面积=2×2×4+1×1×2=18，
故石子落在阴影区域的概率为．
故答案为：．
本题考查了概率，正确运用概率公式是解题的关键．
二、解答题（本大题共3个小题，共30分）
24、（１）x1=1+，x2=1−；（２）x1=-1,x2=1．
【解析】
（１）在本题中，把常数项-4移项后，应该在左右两边同时加上一次项系数-2的一半的平方，配方后即可解答．
（２）利用直接开方法得到，然后解两个一次方程即可．
【详解】
（１）解：由原方程移项，得x2-2x=4，
等式两边同时加上一次项系数一半的平方，得x2−2x+1=5，
配方，得(x−1)2=5，
∴x=1±
∴x1=1+，x2=1−．
（２）解：
或，
∴x1=-1,x2=1．
本题主要考查一元二次方程的解法，掌握解法是解题的关键．
25、（1）利用SAS证明；（2）证明见解析.
【解析】
试题分析：此题考查了平行四边形的判定与性质、矩形的判定以及全等三角形的判定与性质．注意有一个角是直角的平行四边形是矩形，首先证得四边形ABCD是平行四边形是关键．（1）由在□ABCD中，AE=CF，可利用SAS判定△ADE≌△CBF．（2）由在▱ABCD中，且AE=CF，利用一组对边平行且相等的四边形是平行四边形，可证得四边形DEBF是平行四边形，又由∠DEB=90°，可证得四边形DEBF是矩形．
试题解析：（1）∵四边形ABCD是平行四边形，
∴AD=CB，∠A=∠C，
在△ADE和△CBF中，
，
∴△ADE≌△CBF（SAS）．
（2）∵四边形ABCD是平行四边形，
∴AB=CD，AB∥CD，
∵AE=CF，∴BE=DF，
∴四边形ABCD是平行四边形，
∵∠DEB=90°，∴四边形DEBF是矩形．
故答案为（1）利用SAS证明；（2）证明见解析.
考点：平行四边形的性质；全等三角形的判定与性质；矩形的判定．
26、（1）；（2）①2x，x；②S(0＜x≤)．
【解析】
（1）根据勾股定理可得AC=，进而根据正方形对角线相等而且互相平分，可得AM的长；
（2）由中点定义可得AP=2PQ，AQ=PQ，然后由正方形与△ABD公共部分可得是以QM为高的等腰直角三角形，据此即可解答．
【详解】
解：（1）∵正方形ABCD的边长为4，
∴对角线AC4，
又∴AM2．
故答案为：2．
（2）①Q是AP的中点，设PQ=x，
∴AP=2PQ=2x，AQ=x．
故答案为：2x；x．
②如图：
∵以PQ为对角线作正方形，
∴∠GQM=∠FQM=45°
∵正方形ABCD对角线AC、BD交于点M，
∴∠FMQ=∠GMQ=90°，
∴△FMQ和△GMQ均为等腰直角三角形，
∴FM=QM=MG．
∵QM=AM﹣AQ=2x，
∴SFG•QM，
∴S，
∵依题意得：，
∴0＜x≤2，
综上所述：S(0＜x≤2)，
本题考查了正方形的性质：正方形的四条边都相等，四个角都是直角；正方形的两条对角线相等，互相垂直平分，并且每条对角线平分一组对角．解答本题要充分利用等腰直角三角形性质解答．
题号
一
二
三
四
五
总分
得分
批阅人