浙江省绍兴市诸暨市暨阳初级中学2025届九上数学开学达标检测模拟试题【含答案】

这是一份浙江省绍兴市诸暨市暨阳初级中学2025届九上数学开学达标检测模拟试题【含答案】，共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）已知△ABC和△A′B′C′是位似图形．△A′B′C′的面积为6cm2，周长是△ABC的一半．AB＝8cm，则AB边上高等于 （ ）
A．3 cm B．6 cm C．9cm D．12cm
2、（4分）如图，在中，点、、分别在边、、上，且，．下列说法中不正确的是（ ）
A．四边形是平行四边形
B．如果，那么四边形是矩形．
C．如果平分，那么四边形是正方形．
D．如果且，那么四边形是菱形．
3、（4分）某校八年级有452名学生，为了了解这452名学生的课外阅读情况，从中抽取50名学生进行统计．在这个问题中，样本是（ ）
A．452名学生B．抽取的50名学生
C．452名学生的课外阅读情况D．抽取的50名学生的课外阅读情况
4、（4分）若把分式的x、y同时扩大3倍，则分式值（ ）
A．不变B．扩大为原来的3倍C．缩小为原来的D．扩大为原来的9倍
5、（4分）下列运算错误的是
A．B．
C．D．
6、（4分）如图，把一个长方形的纸片对折两次，然后剪下一个角，为了得到一个钝角为的菱形，剪口与折痕所成的角的度数为（）
A．B．
C．D．
7、（4分）如图，直线y=-x+2与x轴交于点A，则点A的坐标是（ ）
A．（2,0）B．（0,2）C．（1,1）D．（2,2）
8、（4分）某学校拟建一间矩形活动室，一面靠墙(墙足够长)，中间用一道墙隔开，并在如图所示的三处各留1m宽的门，已知计划中的材料可建墙体(不包括门)总长为27m，建成后的活动室面积为75m2，求矩形活动室的长和宽，若设矩形宽为x，根据题意可列方程为( )
A．x(27﹣3x)＝75B．x(3x﹣27)＝75
C．x(30﹣3x)＝75D．x(3x﹣30)＝75
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）已知反比例函数，当时，y的取值范围是________．
10、（4分）计算：＝_____；|﹣|＝_____．
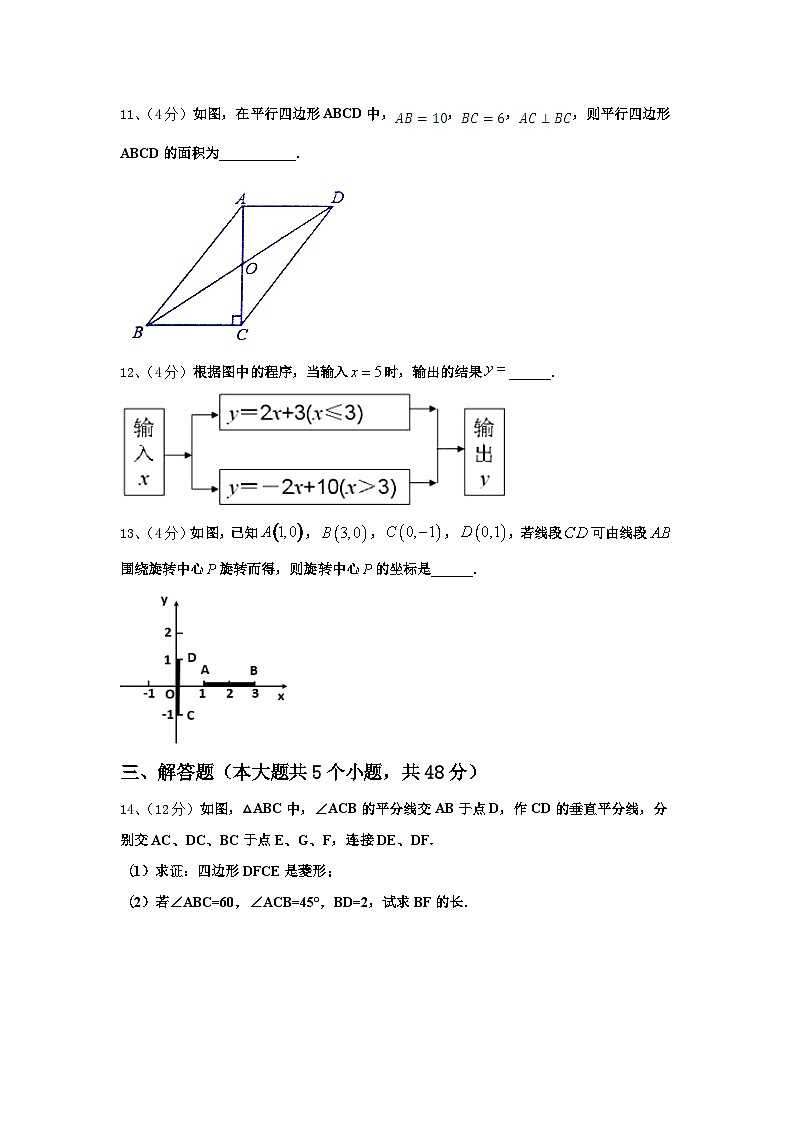
11、（4分）如图，在平行四边形ABCD中，，，，则平行四边形ABCD的面积为___________.
12、（4分）根据图中的程序，当输入时，输出的结果______.
13、（4分）如图，已知，，，，若线段可由线段围绕旋转中心旋转而得，则旋转中心的坐标是______.
三、解答题（本大题共5个小题，共48分）
14、（12分）如图，△ABC中，∠ACB的平分线交AB于点D，作CD的垂直平分线，分别交AC、DC、BC于点E、G、F，连接DE、DF．
（1）求证：四边形DFCE是菱形；
（2）若∠ABC=60，∠ACB=45°，BD=2，试求BF的长．
15、（8分） “中华人民共和国道路交通管理条例”规定：小汽车在高速公路上的行驶速度不得超过120千米/小时，不得低于60千米/小时，如图，一辆小汽车在高速公路上直道行驶，某一时刻刚好行驶到“车速检测点”正前方60米处，过了3秒后，测得小汽车位置与“车速检测点”之间的距离为100米，这辆小汽车是按规定行驶吗？
16、（8分）如图，从电线杆离地面5m处向地面拉一条长13m的缆绳，这条缆绳在地面的固定点距离电线杆底部有多远？
17、（10分）为积极响应新旧功能转换，提高公司经济效益，某科技公司近期研发出一种新型高科技设备，每台设备成本价为30万元，经过市场调研发现，每台售价为35万元时，年销售量为550台；每台售价为40万元时，年销售量为500台.假定该设备的年销售量（单位：台）和销售单价（单位：万元）成一次函数关系.
（1）求年销售量与销售单价的函数关系式；
（2）根据相关规定，此设备的销售单价不得高于60万元，如果该公司想获得8000万元的年利润，则该设备的销售单价应是多少万元？
18、（10分）如图，在平面直角坐标系中，直线y＝﹣x+3与x轴交于点C与直线AD交于点A(1，2)，点D的坐标为(0，1)
(1)求直线AD的解析式；
(2)直线AD与x轴交于点B，请判断△ABC的形状；
(3)在直线AD上是否存在一点E，使得4S△BOD＝S△ACE，若存在求出点E的坐标，若不存在说明理由．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）若分式的值是0，则x的值为________．
20、（4分）在直角ΔABC中，∠BAC=90°，AC=3，∠B=30°，点D在BC上，若ΔABD为等腰三角形，则BD=___________．
21、（4分）如图，已知∠AON＝40°，OA＝6，点P是射线ON上一动点，当△AOP为直角三角形时，∠A＝_____°．
22、（4分）如图，直线l1：y=x+n–2与直线l2：y=mx+n相交于点P(1，2)．则不等式mx+n1
【解析】
∵直线l1：y＝x＋n－2与直线l2：y＝mx＋n相交于点P(1，2)，
∴关于x的不等式mx＋n＜x＋n－2的解集为x>1，
故答案为x>1.
23、1
【解析】
根据直角三角形的性质（斜边上的中线等于斜边的一半），求出DM=AB=3，即可得到ME=1，根据题意求出DE=DM+ME=4，根据三角形中位线定理可得BC=2DE=1．
【详解】
解：∵AM⊥BM，点D是AB的中点，
∴DM=AB=3，
∵ME=DM，
∴ME=1，
∴DE=DM+ME=4，
∵D是AB的中点，DE∥BC，
∴BC=2DE=1，
故答案为：1．
点睛：本题考查的是三角形的中位线定理的应用，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键．
二、解答题（本大题共3个小题，共30分）
24、【几何背景】：详见解析；【知识迁移】：详见解析；【拓展应用】：
【解析】
几何背景：由 Rt△ABD中，AD1＝AB1﹣BD1，Rt△ACD中，AD1＝AC1﹣CD1，则结论可证．
知识迁移：过P点作PE⊥AD，延长EP交BC于F，可证四边形ABFE，四边形DCFE是矩形．根据上面的结论求得PA、PB、PC、PD之间的数量关系．
拓展应用：根据勾股定理可列方程组，可求PD＝c，PC＝c即可得.
【详解】
解：几何背景：在Rt△ABD中，AD1＝AB1﹣BD1
Rt△ACD中，AD1＝AC1﹣CD1，
∴AB1﹣BD1＝AC1﹣CD1，
∴AB1﹣AC1＝BD1﹣CD1．
知识迁移：BP1﹣PC1 ＝BF1﹣CF1．
如 图：
过P点作PE⊥AD，延长EP交BC于F
∴四边形ABCD是矩形
∴AD∥BC∠BAD＝∠ADC＝∠DCB＝∠ABC＝90°
又∵PE⊥AD
∴PF⊥BC
∵PE是△APD的高
∴PA1﹣PD1＝AE1﹣DE1．
∵PF是△PBC的高
∴BP1﹣PC1 ＝BF1﹣CF1．
∵∠BAD＝∠ADC＝∠DCB＝∠ABC＝90°，PE⊥AD，PF⊥BC
∴四边形ABFE，四边形DCFE是矩形
∴AE＝BF，CF＝DE
∴PA1﹣PD1＝BP1﹣PC1．
拓展应用：∵PA1﹣PD1＝BP1﹣PC1．
∴PA1﹣PB1＝c1．
∴PD1﹣PC1＝c1．
且PD1+PC1＝c1．
∴PD＝c，PC＝c
∴，
故答案为.
本题考查了四边形的综合题，矩形的性质，勾股定理，关键是利用勾股定理列方程组．
25、（1）；（2）或；(3),理由见解析。
【解析】
（1）联立两函数即可求出C点坐标;
（2）根据题意写出M,D,E的坐标，再根据即可列式求解；
（3）过作，交的延长线于，设交于点，得到得为等腰直角三角形，再证明，故可得，即可求解.
【详解】
（1）联立，解得
∴
（2）
依题意得
解得或
(3),理由如下：
过作，交的延长线于，设交于点
易得为等腰直角三角形，
易得
此题主要考查一次函数的应用，解题的关键是根据题意作出辅助线、熟知一次函数的图像及全等三角形的判定与性质.
26、（1）、、，作图见解析；（2）6
【解析】
（1）利用关于原点对称的点的坐标特征写出点A1、B1、C1的坐标，然后描点即可得到△A1B1C1；
（2）利用三角形面积公式计算．
【详解】
解：（1）如图，△A1B1C1为所作，
∴、、；
（2）；
本题考查三角形的面积计算，难度不大，解决本题的关键是正确掌握关于原点对称的点的坐标的特点．
题号
一
二
三
四
五
总分
得分