高中数学人教B版 (2019)必修 第四册第九章 解三角形9.2 正弦定理与余弦定理的应用教课课件ppt

这是一份高中数学人教B版 (2019)必修 第四册第九章 解三角形9.2 正弦定理与余弦定理的应用教课课件ppt，共53页。PPT课件主要包含了新知初探·自主学习，课堂探究·素养提升，顺时针，°～360°，答案B，解析由图知α＝β，答案D等内容，欢迎下载使用。
课程标准能用正弦定理、余弦定理解决简单的实际问题．
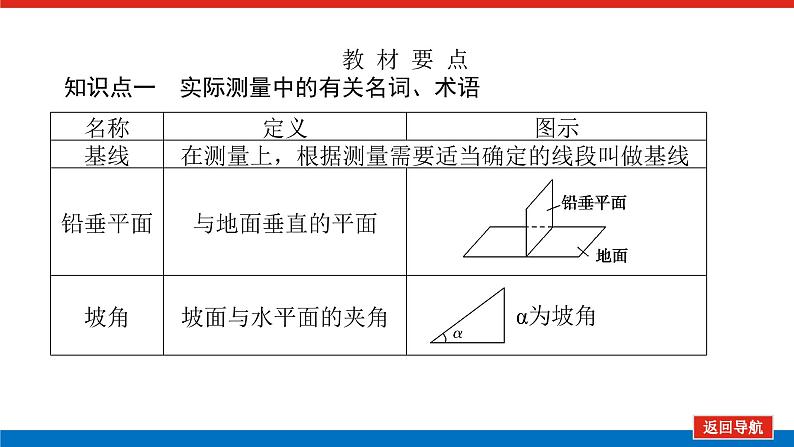
教 材 要 点知识点一　实际测量中的有关名词、术语
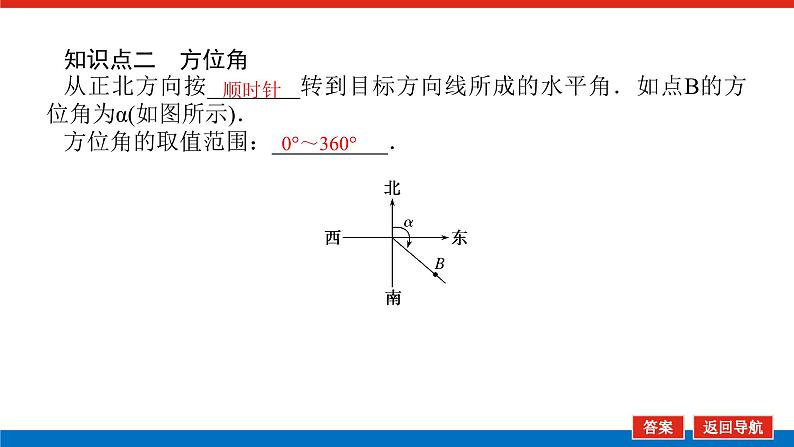
知识点二　方位角从正北方向按________转到目标方向线所成的水平角．如点B的方位角为α(如图所示)．方位角的取值范围：__________．
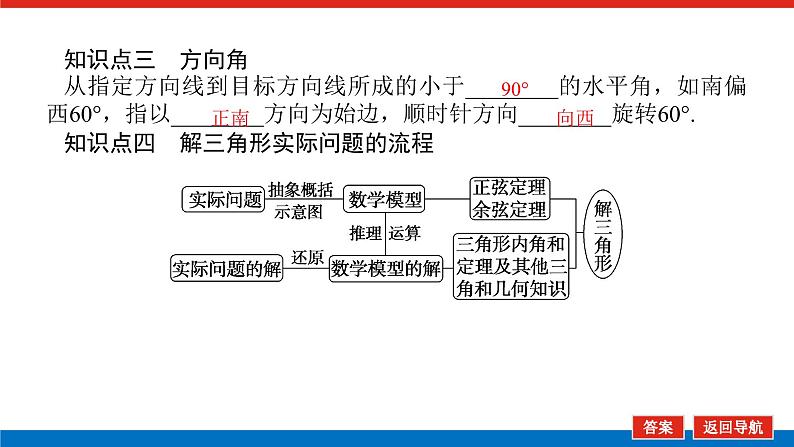
知识点三　方向角从指定方向线到目标方向线所成的小于________的水平角，如南偏西60°，指以________方向为始边，顺时针方向________旋转60°.知识点四　解三角形实际问题的流程
基 础 自 测1．从A处望B处的仰角为α，从B处望A处的俯角为β，则α，β的关系为(　　)A．α>β B．α＝βC．α＋β＝90° D．α＋β＝180°
3．甲、乙两楼相距20 m，从乙楼底望甲楼顶的仰角为60°，从甲楼顶望乙楼顶的俯角为30°，则甲、乙两楼的高分别是________m、________m．
将题中距离、角度转化到一个三角形中，再利用正弦、余弦定理解三角形．
方法归纳测量两个不可到达的点之间的距离，一般是把求距离问题转化为应用余弦定理求三角形的边长问题，然后把求未知的另外边长问题转化为只有一点不能到达的两点距离测量问题，运用正弦定理解决．
跟踪训练1　在相距2千米的A，B两点处测量目标C，若∠CAB＝75°，∠CBA＝60°，求A，C两点之间的距离为________千米．
题型2　测量高度问题例2　(1)某兴趣小组要测量电视塔AE的高度H(单位：m)．如图所示，竖直放置的标杆BC的高度h＝4 m，仰角∠ABE＝α，∠ADE＝β.该小组已测得一组α，β的值，算出了tan α＝1.24，tan β＝1.20，请据此算出H的值．
状元随笔　①求出∠CBD＝45 °，在△BCD中利用正弦定理进行求解．②先在△BCD中利用正弦定理求出BC的长度，进而利用正切值求出塔高AB.
方法归纳解决测量高度问题的一般步骤(1)画图：根据已知条件画出示意图．(2)分析三角形：分析与问题有关的三角形．(3)求解：运用正、余弦定理，有序地解相关的三角形，逐步求解．在解题中，要综合运用立体几何知识与平面几何知识，注意方程思想的运用．
(2)如图，在离地面高400 m的热气球上，观测到山顶C处的仰角为15°，山脚A处的俯角为45°，已知∠BAC＝60°，求山的高度BC.
题型3　求航向的角度例3　某渔轮在航行中不幸遇险，发出呼救信号，我海军舰艇在A处获悉后，立即测出该渔轮在方位角为45°，距离为10 n mile的C处，并测得渔轮正沿方位角为105°的方向，以9 n mile/h的速度向某小岛靠拢，我海军舰艇立即以21 n mile/h的速度前去营救，求舰艇的航向和靠近渔轮所需的时间．
状元随笔　本题中所涉及的路程在不断变化，但舰艇和渔轮相遇时所用时间相等，先设出所用时间t，找出等量关系，然后解三角形．
例4　如图所示，一辆汽车从O点出发沿一条直线公路以50公里/小时的速度匀速行驶(图中的箭头方向为汽车行驶方向)，汽车开动的同时，在距汽车出发点O点的距离为5公里、距离公路线的垂直距离为3公里的M点的地方有一个人骑摩托车出发想把一件东西送给汽车司机．问骑摩托车的人至少以多大的速度匀速行驶才能实现他的愿望，此时他驾驶摩托车行驶了多少公里？
方法归纳解决实际问题应注意的问题(1)首先明确题中所给各个角的含义，然后分析题意，分析已知与所求，再根据题意画出正确的示意图，这是最关键最主要的一步．(2)将实际问题转化为可用数学方法解决的问题后，要正确使用正、余弦定理解决问题．
跟踪训练5　(1)在△ABC中，角A，B，C所对的边分别为a，b，c，且a sin 2B＋b sin A＝0.①求角B；②若c＝2，A为△ABC的最小角，求△ABC周长的取值范围．
①利用正弦定理、两角和的正弦公式化简已知条件，求得cs B，进而求得B.②结合正弦定理、三角恒等变换、三角函数的值域，求得a＋b的取值范围，从而求得△ABC周长的取值范围．
(2)已知在△ABC中，∠A＝120°，∠A的角平分线与BC相交于点D.①若AC＝2AB＝2，求CD的长；②若AD＝1，求△ABC面积的最小值．
教材反思1．利用正弦定理、余弦定理可以解决一个可以到达的点与另一个不可以到达的点之间的距离问题(一般利用正弦定理，解一个三角形即可)，还可以解决两个不可到达的点之间的距离问题．解决此类问题，先利用测量工具测出所构造的三角形的有关的边和角，再通过解三角形求相应距离．2．利用正弦定理、余弦定理可以解决底(顶)部不能到达的物体的高度问题或者是航海航天中的角度问题．解决此类问题的策略是先把立体几何问题转化为平面几何问题，再通过解一个直角三角形和一个斜三角形或两个直角三角形使问题得解．