






高中数学人教B版 (2019)必修 第四册第十章 复数10.1 复数及其几何意义10.1.1 复数的概念教案配套课件ppt
展开课程标准1.通过方程的解,认识复数.2.理解复数的代数表示,理解两个复数相等的含义.
教 材 要 点知识点一 复数的有关概念1.复数(1)定义:设a,b都是实数,形如a+bi的数叫做复数,其中i叫做________,满足i2=________,a叫做复数的________,b叫做复数的________.(2)表示方法:复数通常用__________表示,即z=a+bi(a,b∈R),这一表示形式叫做复数的代数形式.2.复数集(1)定义:________所构成的集合叫做复数集.(2)表示:通常用大写字母C表示.
基 础 自 测1.判断(正确的打“√”,错误的打“×”)(1)若a,b为实数,则z=a+bi为虚数.( )(2)若a∈R,则(a+1)i是纯虚数.( )(3)两个虚数不能比较大小.( )
解析:错误.若b=0,则z=a+bi为实数.
解析:错误.当a=-1时,(a+1)i不是纯虚数.
解析:2-bi的实部为2,虚部为-b,由题意知2=-(-b),所以b=2.
解析:由复数定义知C正确.
4.已知(2m-5n)+3i=3n-(m+5)i,m,n∈R,则m+n=________.
题型1 复数的有关概念例1 (1)下列命题中,真命题的个数是( )①若x,y∈C,则x+yi=1+i的充要条件是x=y=1;②若a,b∈R且a>b,则a+i>b+i;③若x2+y2=0,则x=y=0.A.0 B.1 C.2 D.3
【解析】 ①由于x,y∈C,所以x+yi不一定是复数的代数形式,不符合复数相等的充要条件,所以①是假命题.②由于两个虚数不能比较大小,所以②是假命题.③当x=1,y=i时,x2+y2=0成立,所以③是假命题.
(2)给出下列三个命题:①若z∈C,则z2≥0;②2i-1虚部是2i;③2i的实部是0.其中真命题的个数为( )A.0 B.1 C.2 D.3
【解析】 对于①,当z∈R时,z2≥0成立,否则不成立,如z=i,z2=-1<0,所以①为假命题;对于②,2i-1=-1+2i,其虚部为2,不是2i,所以②为假命题;对于③,2i=0+2i, 其实部是0,所以③为真命题.
首先将所给的复数化简为复数的代数形式,然后根据实部与虚部的概念确定实部、虚部.
方法归纳1.正确理解复数的有关概念是解答复数概念题的关键,另外在判断命题的正确性时,需通过逻辑推理加以证明,但否定一个命题的正确性时,只需举一个反例即可,所以在解答这类题型时,可按照“先特殊,后一般”“先否定,后肯定”的方法进行解答.2.准确理解复数的实部与虚部的概念复数a+bi(a,b∈R)中,实数a和b分别叫做复数的实部和虚部.特别注意,b为复数的虚数单位的系数,b连同它的符号叫做复数的虚部.
跟踪训练1 (1)复数a+bi(a,b∈R)为纯虚数是a=0的_________条件.
解析:若a+bi为纯虚数,则必有a=0,故为充分条件;但若a=0且b=0时,a+bi=0为实数,故不是必要条件.
根据复数z为实数、虚数及纯虚数的充要条件列方程(不等式)组求解.
方法归纳利用复数的代数形式对复数分类时,关键是根据分类标准列出实部、虚部应满足的关系式(等式或不等式(组)),求解参数时,注意考虑问题要全面.
题型3 复数相等的条件例3 (1)已知2x-1+(y+1)i=x-y+(-x-y)i,求实数x,y的值. 根据复数相等的充要条件求解. (2)已知关于x的方程(x2+x+3m)-(2x+1)i=0有实数根,求实数m的值.
方法归纳应用复数相等的充要条件时,要注意:(1)必须是复数的代数形式才可以根据实部与实部相等,虚部与虚部相等列方程组.(2)利用这一结论,可以把“复数相等”这一条件转化为两个实数等式,为应用方程思想提供了条件,同时这也是复数问题实数化思想的体现,这一思想在解决复数问题中非常重要.
跟踪训练3 (1)若(2x2-3x-2)+(x2-5x+6)i=0,求实数x的值;
题型4 复数的不相等关系【思考探究】 1.4+2i>3+i正确吗?[提示] 不正确,如果两个复数不全是实数,那么它们就不能比较大小.2.若(a-2)+bi>0,则实数a,b满足什么条件?[提示] b=0,a>2.
例4 已知复数x2-1+(y+1)i大于复数2x+3+(y2-1)i,试求实数x,y的取值范围.
状元随笔 两复数若能比较大小,则两复数的虚部都为零.只需满足一复数的实部大于另一复数的实部.
跟踪训练4 若复数z=(m+1)+(m2-9)i<0,则实数m的值等于________.
高中数学人教B版 (2019)必修 第四册第十章 复数10.1 复数及其几何意义10.1.1 复数的概念课文ppt课件: 这是一份高中数学人教B版 (2019)必修 第四册第十章 复数10.1 复数及其几何意义10.1.1 复数的概念课文ppt课件,文件包含人教B版高中数学必修第四册第10章1011复数的概念课件ppt、人教B版高中数学必修第四册第10章1011复数的概念学案doc、人教B版高中数学必修第四册课后素养落实4复数的概念含答案doc等3份课件配套教学资源,其中PPT共49页, 欢迎下载使用。
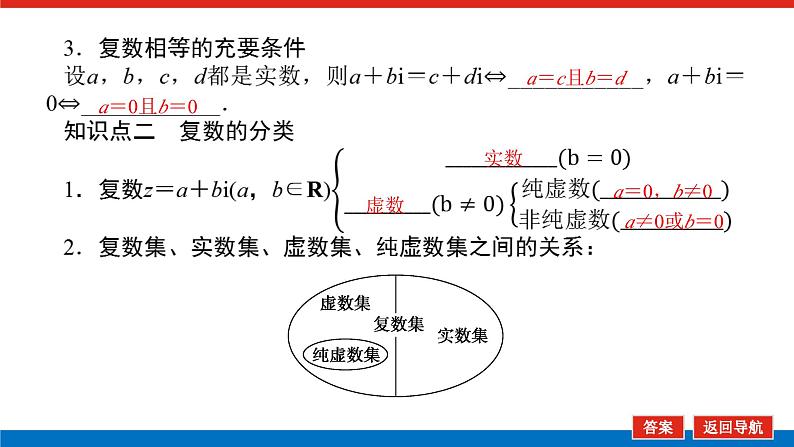
人教B版 (2019)必修 第四册10.1.1 复数的概念课文ppt课件: 这是一份人教B版 (2019)必修 第四册10.1.1 复数的概念课文ppt课件,共47页。PPT课件主要包含了a≠0,b=0,a=0,b≠0,a=c且b=d,复数的概念,复数的分类,复数相等的充要条件等内容,欢迎下载使用。
高中数学10.1.1 复数的概念授课ppt课件: 这是一份高中数学10.1.1 复数的概念授课ppt课件,共30页。













