浙江省杭州市拱墅区华东师大附属杭州中学2023—2024学年上学期期中考试八年级数学试卷

这是一份浙江省杭州市拱墅区华东师大附属杭州中学2023—2024学年上学期期中考试八年级数学试卷，共24页。
A．B．
C．D．
2．下列长度的3根小木棒不能搭成三角形的是
A．，，B．，，C．，，D．，，
3．已知关于的不等式的解在数轴上表示如图所示，则这个不等式的解集为
A．B．C．D．
4．如图，作的边上的高，以下作法正确的是
A．B．
C．D．
5．在△中，，是底边上的高，下面结论不一定成立的是
A．B．C．平分D．
6．如果将一副三角板按如图方式叠放，那么等于
A．B．C．D．
7．为说明命题“若，则”是假命题，所列举的反例正确的是
A．，B．，C．，D．，
8．已知一个直角三角形的周长是，斜边上中线长为2，则这个三角形的面积为
A．5B．2C．D．1
9．对于分式，为常数），若当时，该分式总有意义；当时，该分式的值为负数．则，与0的大小关系正确的是
A．B．C．D．
10．如图，在△中，，，，分别为线段，上一点，且，连接、交于点，延长交于点．以下四个结论正确的是
①；
②若，则；
③若平分，则；
④连结，若，则．
A．①②③B．③④C．①②④D．①②③④
二、填空题
11．用不等式表示“的7倍减去1是正数”就是 ．
12．命题“同位角相等，两直线平行”的逆命题是： ．
13．如图，在中，平分，，则 ．
14．甲乙两位同学进行一种数学游戏．游戏规则是：两人轮流对△及△对应的边或角添加等量条件（点，，分别是点，，的对应点）．某轮添加条件后，若能判定△与△全等，则当轮添加条件者失败，另一人获胜．如表记录了两人游戏的部分过程，则下列说法正确的是 （填写所有正确结论的序号）．
15．如图，已知四边形中，，，，，，则四边形的面积为 ．
16．三个非负实数，，满足，，则的取值范围是 ，的取值范围是 ．
三、解答题
17．解下列一元一次不等式（组．
（1）；
（2）（把解在数轴上表示出来）．
18．在中，，利用直尺和圆规作图．
（1）作出的角平分线；
（2）若，，求出斜边上的高的长度．
19．已知方程组的解满足为非正数，为负数．
（1）求的取值范围；
（2）在（1）的条件下，若不等式的解为．求的值．
20．如图，△中，，，为延长线上一点，点在上，且．
（1）求证：；
（2）若，求的度数．
21．如图，在中，是的高线，是的角平分线，已知．
（1）若，求的度数；
（2）设，用含有的代数式表示的大小．
22．某电器超市销售每台进价分别为200元、170元的、两种型号的电风扇，如表是近两周的销售情况：
（1）求、两种型号的电风扇的销售单价；
（2）若进价、售价均保持不变，超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台，求种型号的电风扇最多能采购多少台？
（3）在（2）的条件下，利用不等式的基本性质说明超市销售完这30台电风扇的利润无法超过1300元的目标．（利润销售总收入进货总价）
23．已知在中，，且．作，使得．
（1）如图1，若与互余，则 （用含的代数式表示）；
（2）如图2，若与互补，过点作于点，求证：；
（3）若与的面积相等，则与满足什么关系？请直接写出你的结论．
2023-2024学年浙江省华东师大附属杭州学校八年级（上）期中数学试卷
参考答案与试题解析
一.选择题：本大题有10个小题，在每小题给出的四个选项中，只有一项是符合题目要求的.
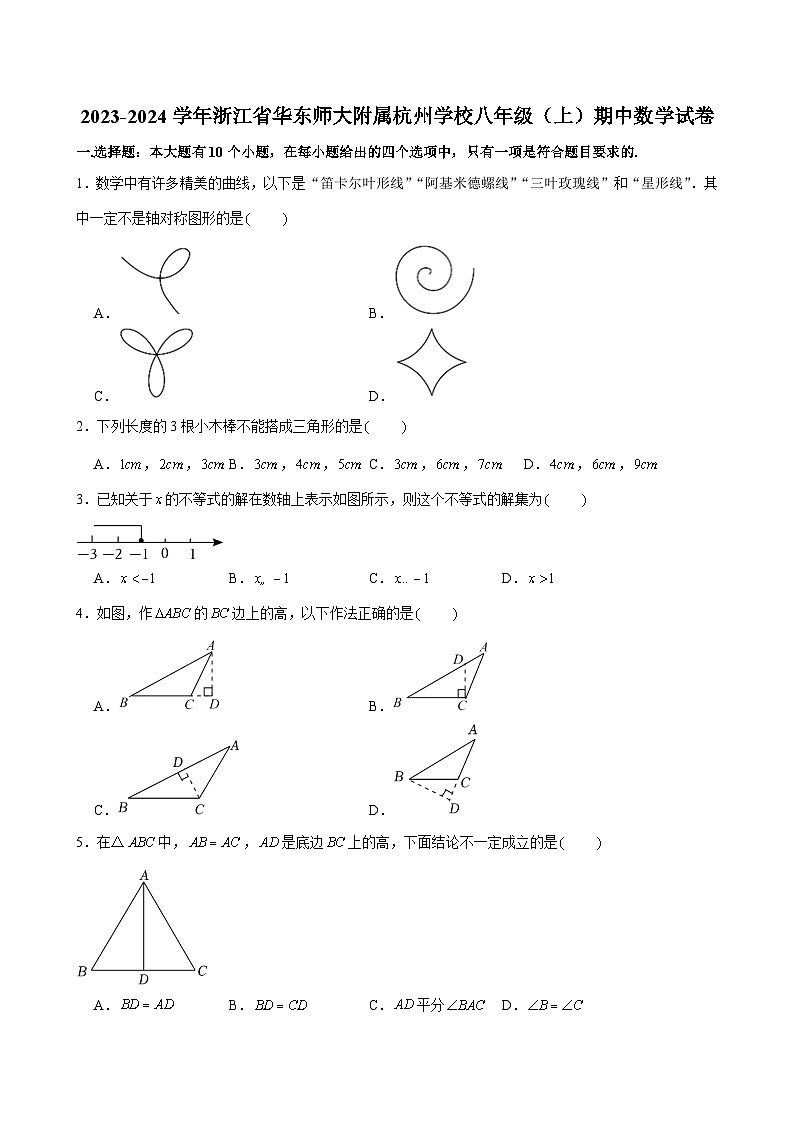
1．数学中有许多精美的曲线，以下是“笛卡尔叶形线”“阿基米德螺线”“三叶玫瑰线”和“星形线”．其中一定不是轴对称图形的是
A．B．
C．D．
【分析】根据如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．
【解答】解：，，选项中的图形都能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以是轴对称图形；
选项中的图形不能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形；
故选：．
【点评】本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
2．下列长度的3根小木棒不能搭成三角形的是
A．，，B．，，C．，，D．，，
【分析】在运用三角形三边关系判定三条线段能否构成三角形时，只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形，由此即可判断．
【解答】解：、，不能搭成三角形，故符合题意；
、，能搭成三角形，故不符合题意；
、，能搭成三角形，故不符合题意；
、，能搭成三角形，故不符合题意．
故选：．
【点评】本题考查三角形三边关系，关键是掌握三角形三边关系定理．
3．已知关于的不等式的解在数轴上表示如图所示，则这个不等式的解集为
A．B．C．D．
【分析】根据解不等式，不等式的解集在数轴上表示出来，向右画；，向左画），可得答案．
【解答】解：由数轴可得不等式的解集为：．
故选：．
【点评】本题考查在数轴上表示不等式的解集，在表示解集时“”，“ ”要用实心圆点表示；“”，“ ”要用空心圆点表示．
4．如图，作的边上的高，以下作法正确的是
A．B．
C．D．
【分析】根据三角形的高的定义判断即可．
【解答】解：如图，选项中，线段是边上的高．
故选：．
【点评】本题考查作图基本作图，三角形的高等知识，解题的关键是掌握三角形的高的定义，属于中考常考题型．
5．在△中，，是底边上的高，下面结论不一定成立的是
A．B．C．平分D．
【分析】根据等“腰三角形底边上的高，底边上的中线，顶角的平分线重合”即可对选项，，进行判断，再根据当时，则，由此可得出答案．
【解答】解：在△中，，是底边上的高，
，平分，，
故选项，，一定成立，不符合题意；
当时，则，
选项不一定成立，符合题意．
故选：．
【点评】此题主要考查了等腰三角形的性质，熟练掌握等腰三角形“三线合一”的性质是解决问题的关键．
6．如果将一副三角板按如图方式叠放，那么等于
A．B．C．D．
【分析】先求出，再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解．
【解答】解：如图，，
由三角形的外角性质得，，
，
．
故选：．
【点评】本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质，熟记性质是解题的关键．
7．为说明命题“若，则”是假命题，所列举的反例正确的是
A．，B．，C．，D．，
【分析】找到一个满足题设但不满足结论的、的值即可．
【解答】解：当，时满足，但，，，，
故选：．
【点评】本题考查命题与定理，解题的关键是理解题意，灵活运用所学知识解决问题．
8．已知一个直角三角形的周长是，斜边上中线长为2，则这个三角形的面积为
A．5B．2C．D．1
【分析】根据直角三角形的性质：在直角三角形中，斜边上的中线等于斜边的一半，可求得斜边的长，再根据直角三角形的周长和勾股定理，可求得两直角边的长或长的乘积，由此可求出这个三角形的面积．
【解答】解：设两直角边分别为，，斜边为，
根据三角形的性质知：，
可得：．
故．
故选：．
【点评】在解题过程中，应了解直角三角形的一些特殊性质，在进行求解的时候使问题变得简单．
9．对于分式，为常数），若当时，该分式总有意义；当时，该分式的值为负数．则，与0的大小关系正确的是
A．B．C．D．
【分析】利用分式成立的条件判断有可能为正，则，再根据时，分式值为负，可判断、异号．
【解答】解：当时，该分式总有意义，
说明当时，分母有可能为0，
为正数，即，
又时，该分式的值为负数，
，即，
、异号，
，
只有选项正确，
故选：．
【点评】本题考查了分式的值，分式成立的条件，解题的关键是掌握分式的值，分式成立的条件．
10．如图，在△中，，，，分别为线段，上一点，且，连接、交于点，延长交于点．以下四个结论正确的是
①；
②若，则；
③若平分，则；
④连结，若，则．
A．①②③B．③④C．①②④D．①②③④
【分析】由“”可证△△，可得，可证，可得，则点是的中垂线上，由线段垂直平分线的性质可得，故①正确；
由全等三角形的性质可得，由直角三角形的性质可得，故②正确；
由角平分线的性质可证点是角平分线的交点，可得点到三边距离相等，由面积法可求，故③正确；
由等腰三角形的性质和三角形内角和定理可得，由，可得，故④错误，即可求解．
【解答】解：在△和△中，
，
△△，
，
，
，
，
，
点是的中垂线上，
，
点在的中垂线上，
垂直平分，
，故①正确；
若，则，
△△，
，
，
又，
，故②正确；
若平分，
，
，，
，
点是角平分线的交点，
点到三边的距离为的长，
，，，
，
，
，
，故③正确；
如图，连接，
若，则，
△△，
，
，
又，
，
，，
，，
又，
，
，
，
，
，
，
，故④错误，
故选：．
【点评】本题考查了全等三角形的判定和性质，线段垂直平分线的性质，等腰三角形的性质，证明三角形全等三角形是解题的关键．
二、填空题
11．用不等式表示“的7倍减去1是正数”就是 ．
【分析】首先表示“的7倍”为，再表示“减去1”为，最后表示“是正数”为．
【解答】解：由题意得：，
故答案为：．
【点评】此题主要考查了由实际问题抽象出一元一次不等式，用不等式表示不等关系时，要抓住题目中的关键词，如“大于（小于）、不超过（不低于）、是正数（负数）”“至少”、“最多”等等，正确选择不等号．因此建立不等式要善于从“关键词”中挖掘其内涵，不同的词里蕴含这不同的不等关系．
12．命题“同位角相等，两直线平行”的逆命题是： 两直线平行，同位角相等 ．
【分析】把一个命题的题设和结论互换就得到它的逆命题．
【解答】解：命题：“同位角相等，两直线平行．”的题设是“同位角相等”，结论是“两直线平行”．
所以它的逆命题是“两直线平行，同位角相等．”
故答案为：“两直线平行，同位角相等”．
【点评】本题考查了互逆命题的知识，两个命题中，如果第一个命题的条件是第二个命题的结论，而第一个命题的结论又是第二个命题的条件，那么这两个命题叫做互逆命题．其中一个命题称为另一个命题的逆命题．
13．如图，在中，平分，，则 36 ．
【分析】设，根据角平分线定义得出．根据等边对等角以及三角形外角的性质得出，，．然后在中，利用三内角和为列出方程，求出即可．
【解答】解：设，则．
，
，
．
，
．
在中，，
，
，
．
故答案为：36．
【点评】本题考查了角平分线定义，等腰三角形的性质，三角形外角的性质，三角形内角和定理，设，利用表示，，是解题的关键．
14．甲乙两位同学进行一种数学游戏．游戏规则是：两人轮流对△及△对应的边或角添加等量条件（点，，分别是点，，的对应点）．某轮添加条件后，若能判定△与△全等，则当轮添加条件者失败，另一人获胜．如表记录了两人游戏的部分过程，则下列说法正确的是 ①③ （填写所有正确结论的序号）．
【分析】根据全等三角形的判定定理逐一判断即可．
【解答】解：①若第3轮甲添加，根据即可判定△△，则甲失败，乙获胜，故说法正确，符合题意；
②若第3轮甲添加条件，由于含的直角三角形直角边等于斜边的一半，满足，能判定△△，则甲失败，乙获胜，故说法错误，不符合题意；
③若乙第2轮添加条件为，则第3轮甲无论添加任何对应的边或角的等量条件，都能判定△△，则甲失败，乙获胜，故说法正确，符合题意；
故答案为：①③．
【点评】本题重点考查了三角形全等的判定定理，普通两个三角形全等共有四个定理，即、、、，直角三角形可用定理，注意：、不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．
15．如图，已知四边形中，，，，，，则四边形的面积为 36 ．
【分析】根据勾股定理求得的长，再在三角形中可知三边关系为：，可得三角形为直角三角形，然后两三角形的面积和就是所求四边形的面积．
【解答】解：连接，
，，，，，
在直角三角形中有：，即，
，
又，，
，即，
三角形是直角三角形，，
．
故答案为：36．
【点评】此题考查了勾股定理，以及勾股定理的逆定理，三角形的面积公式，熟练掌握勾股定理及勾股定理的逆定理是解本题的关键．
16．三个非负实数，，满足，，则的取值范围是 ，的取值范围是 ．
【分析】（1）根据，可得，再根据，求出的取值范围即可．
（2）根据已知条件用含的代数式表示，再根据是非负实数，求出的取值范围即可．
【解答】解：，
，
、是非负实数，
，，
，
；
，，
，
，
是非负实数，
，
，
，，
即，
故答案为：；．
【点评】此题主要考查了不等式的性质和应用，以及不等式的解法，要熟练掌握．
三、解答题
17．解下列一元一次不等式（组．
（1）；
（2）（把解在数轴上表示出来）．
【分析】（1）依据解不等式的基本步骤依次去括号、移项、合并同类项即可得；
（2）分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．
【解答】解：（1）去括号，得，
移项，得，
合并同类项，得，
（2）解不等式，
得，
解不等式，
得，
则不等式组的解集为，
将解集表示在数轴上如下：
【点评】本题考查的是解一元一次不等式（组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
18．在中，，利用直尺和圆规作图．
（1）作出的角平分线；
（2）若，，求出斜边上的高的长度．
【分析】（1）利用尺规作的角平分线即可．
（2）作于，利用面积法求解即可．
【解答】解：（1）如图，线段即为所求．
（2）作于．
在中，，，
，
．
【点评】本题考查作图复杂作图，角平分线的性质，线段的垂直平分线的性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
19．已知方程组的解满足为非正数，为负数．
（1）求的取值范围；
（2）在（1）的条件下，若不等式的解为．求的值．
【分析】（1）加减消元法解二元一次方程组得，由题意得，，然后解一元一次不等式组即可；
（2）根据不等式的性质可知，，然后求解作答即可．
【解答】详解：（1），
①②得，，
解得，，
将代入①得，，
解得，，
，
为非正数，为负数，
，
解③得，；
解④得，；
不等式组的解集为，
的取值范围为；
（2），
，
不等式的解为，
，即，
的取值为．
【点评】本题考查了加减消元法解二元一次方程组，解一元一次不等式组，不等式的性质．熟练掌握加减消元法解二元一次方程组，解一元一次不等式组，不等式的性质是解题的关键．
20．如图，△中，，，为延长线上一点，点在上，且．
（1）求证：；
（2）若，求的度数．
【分析】（1）运用定理直接证明△△，即可利用全等三角形的性质解决问题．
（2）证明；求出，即可解决问题．
【解答】证明：（1）在△与△中，
，
△△，
，
，
．
（2），，
，
，
，
△△，
；
，，
，
．
【点评】该题主要考查了全等三角形的判定及其性质的应用问题；准确找出图形中隐含的相等或全等关系是解题的关键．
21．如图，在中，是的高线，是的角平分线，已知．
（1）若，求的度数；
（2）设，用含有的代数式表示的大小．
【分析】（1）由题意可求得，再由角平分线的定义可得，即可求的度数；
（2）仿照（1）的解答过程进行求解即可．
【解答】解：（1）在中，，
，
又，是角平分线，
，
；
（2）在中，，
，
又，是角平分线，
，
．
【点评】本题主要考查三角形的内角和定理，解答的关键是结合图形分析清楚各角之间的关系．
22．某电器超市销售每台进价分别为200元、170元的、两种型号的电风扇，如表是近两周的销售情况：
（1）求、两种型号的电风扇的销售单价；
（2）若进价、售价均保持不变，超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台，求种型号的电风扇最多能采购多少台？
（3）在（2）的条件下，利用不等式的基本性质说明超市销售完这30台电风扇的利润无法超过1300元的目标．（利润销售总收入进货总价）
【分析】（1）设种型号电风扇的销售单价为元，种型号电风扇的销售单价为元，根据“销售3台型号5台型号的电风扇，销售收入1800元，销售4台型号10台型号的电风扇，销售收入3100元”，列出二元一次方程组，解方程组即可；
（2）设采购种型号电风扇台，则采购种型号电风扇台，根据金额不多余5400元，列出一元一次不等式，解不等式即可；
（3）设利润超过1300元，列出一元一次不等式，求出，不符合（2）的条件，可知不能实现目标．
【解答】（1）解：设种型号电风扇的销售单价为元，种型号电风扇的销售单价为元，
由题意得：，
解得：，
答：种型号电风扇的销售单价为250元，种型号电风扇的销售单价为210元；
（2）解：设采购种型号电风扇台，则采购种型号电风扇台，
由题意得：，
解得：，
最大为10，
答：种型号的电风扇最多能采购10台；
（3）证明：由题意得：，
解得：，
，
在（2）的条件下，超市销售完这30台电风扇的利润无法超过1300元的目标．
【点评】本题考查了二元一次方程组的应用、一元一次不等式的应用、不等式的性质，解题的关键是：（1）找准等量关系，正确列出二元一次方程组；（2）找出数量关系，正确列出一元一次不等式；（3）找出数量关系，正确列出一元一次不等式．
23．已知在中，，且．作，使得．
（1）如图1，若与互余，则 （用含的代数式表示）；
（2）如图2，若与互补，过点作于点，求证：；
（3）若与的面积相等，则与满足什么关系？请直接写出你的结论．
【分析】（1）由等腰三角形的性质，两角互余的概念，即可求解；
（2）作于，由两角互补的概念，可以证明，即可解决问题；
（3）分两种情况，作于，于，作于，交延长线于，应用三角形全等，可以解决问题．
【解答】（1）解：，
，
与互余，
，
，
故答案为；
（2）证明：作于，
，，
，，，
，
与互补，
，
，
，
，，
，
；
（3）
或与互补；理由如下：
如图1，作于，于，
与的面积相等，
，
，
，
，
；
如图2，作于，交延长线于，
与的面积相等，
，
，
，
，
，
，
，
与互补．
【点评】本题考查等腰三角形的性质，互余，互补的概念，关键是通过辅助线构造全等三角形．
轮次
行动者
添加条件
1
甲
2
乙
3
甲
①若第3轮甲添加，则乙获胜；
②若甲想获胜，第3轮可以添加条件；
②若乙想获胜，科修改第2轮添加条件为．
销售时段
销售数量
销售收入
种型号
种型号
销售收入
第一周
3台
5台
1800元
第二周
4台
10台
3100元
轮次
行动者
添加条件
1
甲
2
乙
3
甲
①若第3轮甲添加，则乙获胜；
②若甲想获胜，第3轮可以添加条件；
②若乙想获胜，科修改第2轮添加条件为．
销售时段
销售数量
销售收入
种型号
种型号
销售收入
第一周
3台
5台
1800元
第二周
4台
10台
3100元