






高中数学人教B版 (2019)必修 第四册第十一章 立体几何初步11.1 空间几何体11.1.6 祖暅原理与几何体的体积评课课件ppt
展开课程标准1.认识柱、锥、台、球及简单组合体的结构特征,能运用这些特征描述现实生活中简单物体的结构.2.知道球、棱柱、棱锥、棱台的体积的计算公式,能用公式解决简单的实际问题.
教 材 要 点知识点一 祖暅原理(1)“幂势既同,则积不容异”,即“夹在两个平行平面间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积________,那么这两个几何体的体积________”.(2)作用:等底面积、等高的两个柱体或锥体的体积________.
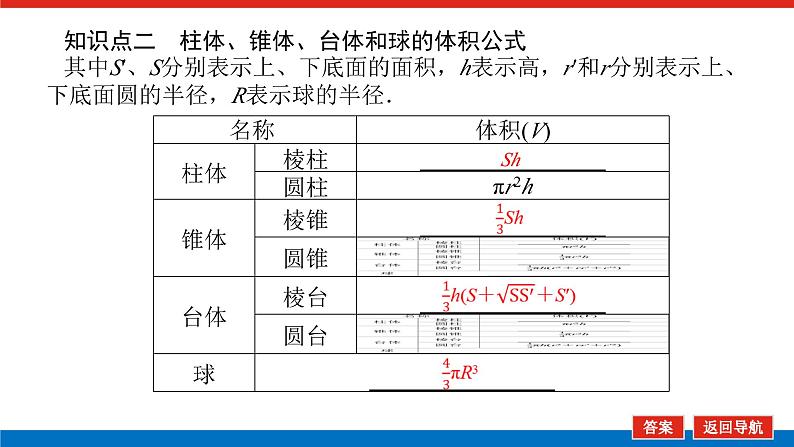
知识点二 柱体、锥体、台体和球的体积公式其中S′、S分别表示上、下底面的面积,h表示高,r′和r分别表示上、下底面圆的半径,R表示球的半径.
基 础 自 测1.若长方体的长、宽、高分别为3 cm、4 cm、5 cm,则长方体的体积为( )A.27 cm3 B.60 cm3C.64 cm3 D.125 cm3
解析:长方体的体积为3×4×5=60(cm3).
2.圆锥的母线长为5,底面半径为3,则其体积为( )A.15π B.30πC.12π D.36π
3.如果轴截面为正方形的圆柱的侧面积是4π,那么圆柱的体积等于( )A.π B.2πC.4π D.8π
解析:设轴截面正方形的边长为a,由题意知S侧=πa·a=πa2.又∵S侧=4π,∴a=2.∴V圆柱=π×2=2π.
4.若一个球的直径是12 cm,则它的体积为________cm3.
题型1 求柱体的体积例1 如图所示的几何体,上面是圆柱,其底面直径为6 cm,高为3 cm,下面是正六棱柱,其底面边长为4 cm,高为2 cm,现从中间挖去一个直径为2 cm的圆柱,求此几何体的体积.
方法归纳计算柱体体积的关键及常用技巧(1)计算柱体体积的关键:确定柱体的底面积和高.(2)常用技巧:①充分利用多面体的截面及旋转体的轴截面,构造直角三角形,从而计算出底面积和高.②由于柱体的体积仅与它的底面积和高有关,而与柱体是几棱柱,是直棱柱还是斜棱柱没有关系,所以我们往往把求斜棱柱的体积通过作垂直于侧棱的截面转化成求直棱柱的体积.
跟踪训练1 一个正方体的底面积和一个圆柱的底面积相等,且侧面积也相等,求正方体和圆柱的体积之比.
(2)如图三棱台ABC-A1B1C1中,AB∶A1B1=1∶2,求三棱锥A1-ABC,三棱锥B-A1B1C,三棱锥C-A1B1C1的体积之比.
(3)如图,已知ABCD-A1B1C1D1是棱长为a的正方体,E为AA1的中点,F为CC1上一点,求三棱锥A1-D1EF的体积.
状元随笔 三棱锥A1-D1EF的高不易求出,可以转换为求三棱锥F-A1D1E的体积.
方法归纳1.三棱柱、三棱台可以分割成三个三棱锥,分割后可求锥体的体积和柱体或台体的体积关系,割补法在立体几何中是一种重要的方法.2.求几何体体积的常用方法
(2)如图,正方体ABCD-A′B′C′D′的棱长为4,动点E,F在棱AB上且EF=2,动点Q在棱D′C′上,则三棱锥A′-EFQ的体积( )A.与点E,F的位置有关B.与点Q的位置有关C.与点E,F,Q的位置都有关D.与点E,F,Q的位置均无关,是定值
(3)如图所示,三棱锥P-ABC的所有棱长都为1,求此三棱锥的体积.
状元随笔 将此三棱锥放在正方体中,看作正方体切去四个三棱锥得到,据此设计算法求解.
题型3 求台体的体积例3 已知正四棱台两底面边长分别为20 cm和10 cm,侧面积是780 cm2.求正四棱台的体积.
【解析】 如图所示,正四棱台ABCD - A1B1C1D1中,A1B1=10 cm,AB=20 cm.取A1B1的中点E1,AB的中点E,则E1E是侧面ABB1A1的高.设O1、O分别是上、下底面的中心,则四边形EOO1E1是直角梯形.
状元随笔 可以尝试借助四棱台内的直角梯形.求出棱台底面积和高,从而求出体积.
方法归纳求台体的体积关键是求出上、下底面的面积和台体的高.要注意充分运用棱台内的直角梯形或圆台的轴截面寻求相关量之间的关系.
跟踪训练3 本例若改为“正四棱台的上、下两底的底面边长分别为2 cm和4 cm,侧棱长为2 cm,求该棱台的体积.”
题型4 求球的体积例4 (1)过球面上三点A,B,C的截面到球心O的距离等于球的半径的一半,且AB=BC=CA=3 cm,求球的体积和表面积.
解决本题要充分利用已知条件,尤其是球半径,截面圆半径和球心距构成的直角三角形.
方法归纳球的基本性质是解决与球有关的问题的依据,球半径、截面圆半径和球心到截面的距离所构成的直角三角形是把空间问题转化为平面问题的主要方法.
跟踪训练4 如果三个球的半径之比是1∶2∶3,那么最大球的体积是其余两个球的体积之和的( )A.1倍 B.2倍C.3倍 D.4倍
教材反思1.本节课的重点是掌握柱体、锥体、台体和球的体积的求法,难点是组合体的表面积.2.本节课要重点掌握的规律方法(1)求空间几何体的体积的方法.(2)求与组合体有关的体积的方法.3.本节课的易错点是求与三视图有关的几何体的体积时,易把相关数据弄错.
高中数学人教B版 (2019)必修 第四册11.1.6 祖暅原理与几何体的体积课文内容课件ppt: 这是一份高中数学人教B版 (2019)必修 第四册<a href="/sx/tb_c4000240_t3/?tag_id=26" target="_blank">11.1.6 祖暅原理与几何体的体积课文内容课件ppt</a>,共34页。PPT课件主要包含了1空间几何体,学习目标,回顾引入,尝试与发现,祖暅原理,讲授新课,柱体的体积,锥体的体积,典例精析,台体的体积等内容,欢迎下载使用。
高中数学人教B版 (2019)必修 第四册11.1.6 祖暅原理与几何体的体积图文课件ppt: 这是一份高中数学人教B版 (2019)必修 第四册11.1.6 祖暅原理与几何体的体积图文课件ppt,文件包含人教B版高中数学必修第四册第11章1116祖暅原理与几何体的体积课件ppt、人教B版高中数学必修第四册第11章1116祖暅原理与几何体的体积学案doc、人教B版高中数学必修第四册课后素养落实14祖暅原理与几何体的体积含答案doc等3份课件配套教学资源,其中PPT共60页, 欢迎下载使用。
高中11.1.6 祖暅原理与几何体的体积图片课件ppt: 这是一份高中11.1.6 祖暅原理与几何体的体积图片课件ppt,共54页。PPT课件主要包含了求柱体的体积,求锥体的体积,求台体的体积,求球的体积等内容,欢迎下载使用。













