四川省泸州市合江县少岷初中2024-2025学年九年级上学期10月月考数学试题

这是一份四川省泸州市合江县少岷初中2024-2025学年九年级上学期10月月考数学试题，共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共12个小题，每小题3分，共36分）
1．下列式子是一元二次方程的是（ ）
A． B． C． D．
2．二次函数（）的图象经过点（0，2），则的值是（ ）
A． B． C．2 D．3
3．一元二次方程的根的情况为（ ）
A．有两个相等的实数根 B．有两个不相等的实数根 C．只有一个实数根 D．没有实数根
4．一元二次方程配方后可变形为（ ）
A． B． C． D．
5．已知二次函数，若当时，；当时，，则a，b的值分别为（ ）
A．， B．， C．， D．，
6．对于二次函数，下列说法正确的是（ ）
A．当，y随x的增大而增大 B．当时，y有最大值
C．图象的顶点坐标为 D．图象与x轴有两个交点
7．二次函数的图象先向左平移4个单位长度，再向下平移2个单位长度后的抛物线解析式为（ ）
A． B． C． D．
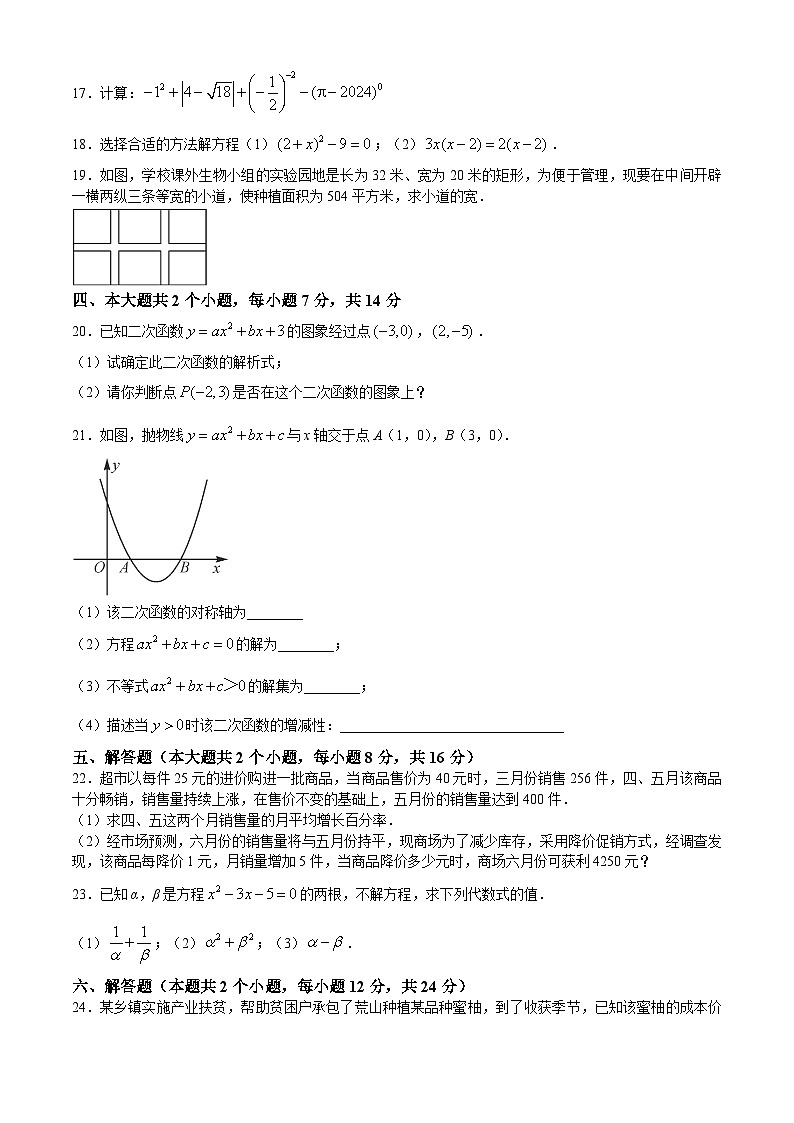
8．国家实施“精准扶贫”政策以来，很多贫困人口走上了致富的道路．某地区2017年底有贫困人口9万人，通过社会各界的努力，2019年底贫困人口减少至1万人．设2017年底至2019年底该地区贫困人口的年平均下降率为x，根据题意列方程得（ ）
A． B． C． D．
9．已知α，β是关于x的一元二次方程的两个不相等的实数根，且满足，则m的值是（ ）
A．3或 B．3 C．1 D．或1
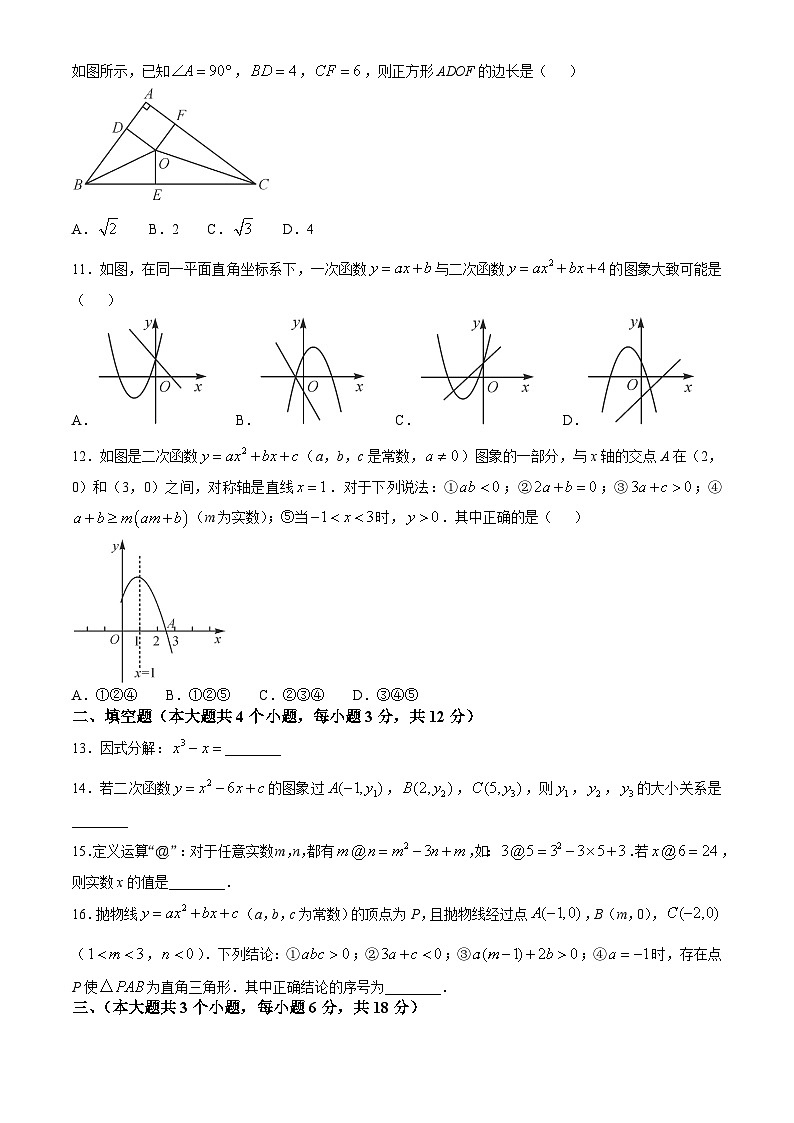
10．我国古代数学家刘徽将勾股形（古人称直角三角形为勾股形）分割成一个正方形和两对全等的三角形，如图所示，已知，，，则正方形ADOF的边长是（ ）
A． B．2 C． D．4
11．如图，在同一平面直角坐标系下，一次函数与二次函数的图象大致可能是（ ）
A． B． C． D．
12．如图是二次函数（a，b，c是常数，）图象的一部分，与x轴的交点A在（2，0）和（3，0）之间，对称轴是直线．对于下列说法：①；②；③；④（m为实数）；⑤当时，．其中正确的是（ ）
A．①②④ B．①②⑤ C．②③④ D．③④⑤
二、填空题（本大题共4个小题，每小题3分，共12分）
13．因式分解：________
14．若二次函数的图象过，，，则，，的大小关系是________
15．定义运算“@”：对于任意实数m，n，都有，如：．若，
则实数x的值是________．
16．抛物线（a，b，c为常数）的顶点为P，且抛物线经过点，B（m，0），（，）．下列结论：①；②；③；④时，存在点P使为直角三角形．其中正确结论的序号为________．
三、（本大题共3个小题，每小题6分，共18分）
17．计算：
18．选择合适的方法解方程（1）；（2）．
19．如图，学校课外生物小组的实验园地是长为32米、宽为20米的矩形，为便于管理，现要在中间开辟一横两纵三条等宽的小道，使种植面积为504平方米，求小道的宽．
四、本大题共2个小题，每小题7分，共14分
20．已知二次函数的图象经过点，．
（1）试确定此二次函数的解析式；
（2）请你判断点是否在这个二次函数的图象上？
21．如图，抛物线与x轴交于点A（1，0），B（3，0）．
（1）该二次函数的对称轴为________
（2）方程的解为________；
（3）不等式的解集为________；
（4）描述当时该二次函数的增减性：________________________________
五、解答题（本大题共2个小题，每小题8分，共16分）
22．超市以每件25元的进价购进一批商品，当商品售价为40元时，三月份销售256件，四、五月该商品十分畅销，销售量持续上涨，在售价不变的基础上，五月份的销售量达到400件．
（1）求四、五这两个月销售量的月平均增长百分率．
（2）经市场预测，六月份的销售量将与五月份持平，现商场为了减少库存，采用降价促销方式，经调查发现，该商品每降价1元，月销量增加5件，当商品降价多少元时，商场六月份可获利4250元？
23．已知α，β是方程的两根，不解方程，求下列代数式的值．
（1）；（2）；（3）．
六、解答题（本题共2个小题，每小题12分，共24分）
24．某乡镇实施产业扶贫，帮助贫困户承包了荒山种植某品种蜜柚，到了收获季节，已知该蜜柚的成本价为8元/千克，投入市场销售时，调查市场行情，发现该蜜柚销售不会亏本，且每天销售量y（千克）与销售单价x（元/千克）之间的函数关系如图所示．
（1）求y与x的函数关系式，并写出x的取值范围；
（2）当该品种的蜜柚定价为多少时，每天销售获得的利润最大？最大利润是多少？
（3）某农户今年共采摘蜜柚4800千克，该品种蜜柚的保质期为40天，根据（2）中获得最大利润的方式进行销售，能否销售完这批蜜柚？请说明理由．
25．（15分）已知二次函数的图象过点A（3，0），．
（1）求二次函数的解析式；
（2）如图，点P是二次函数图象的对称轴上的一个动点，二次函数的图象与y轴交于点B，当最小时，求点P的坐标；
（3）在第一象限内的抛物线上有一点Q，当的面积最大时，求点Q的坐标．
合江少岷初中九年级数学10月静心作业答案
1-5：CCBCB 6-10：BCBBB 11-12CA
13． 14． 15．6或． 16．②③．
17．计算：
解：原式
18．选择合适的方法解方程（1）；（2）．
解：（1），，．（2）原方程变形为，
即，解得，．
19．【解答】设小道的宽为x米，依题意，得
．
整理，得，即．
解得，（舍）．
答：小道的宽为2米．
20．解：（1）由题意，得解得
则二次函数的解析式为．
（2）当时，，
∴点在这个二次函数的图象上．
21．（1） （2），； （3）或；
（4）当时y随x增大而减小，当时y随x的增大而增大
22．（1）解：设平均增长率为x，由题意得：，
解得：或（舍）；
∴四、五这两个月的月平均增长百分率为25％；
（2）解：设降价y元，由题意得：，
整理得：，解得：或（舍）；
∴当商品降价5元时，商场六月份可获利4250元．
23．解：∵α，β是方程的两根，
∴，．
（1）．（2）．
（3）∵．
∴或．
24．解：（1）设y与x的函数关系式为，将（10，200），（15，150）代入，得解得
∴y与x的函数关系式为（）．
（2）设每天销售利润为w元，
则．
∵，
∴当时，w取得最大值，最大值为1210．
答：该品种的蜜柚定价为19元时，每天销售利润最大，最大利润是1210元．
（3）由（2）知，当获得最大利润时，定价为19元/千克，则每天的销售量为千克，
∵保质期为40天，
∴总销售量为千克．
又∵，
∴按（2）中获得最大利润的方式销售，不能销售完这批蜜柚．
25．解：（1）把点A（3，0），代入中，得解得
则抛物线的解析式为．
（2）连接AB，与对称轴交于点P，此时最小．
在中，当时，，则B（0，3）．
设直线AB的解析式为．
∵A（3，0），B（0，3），∴∴
∴直线AB的解析式为．
∵，
∴对称轴是直线．
当时，，
∴P（1，2）．
（3）连接QA，QB，OQ．
设，的面积为S．
根据题意，得
．
∴当时，S最大，此时．