广东省惠州市2024-2025学年八年级上学期月考数学试卷 （10月份）

这是一份广东省惠州市2024-2025学年八年级上学期月考数学试卷 （10月份），共20页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。

1.已知三条线段的长分别是3，7，m，若它们能构成三角形，则整数m的最大值是( )
A. 11B. 10C. 9D. 7
2.在△ABC中，如果∠A：∠B：∠C=1：1：2，那么它是( )
A. 钝角三角形B. 锐角三角形C. 直角三角形D. 等边三角形
3.一个多边形的内角和是1440∘，它是一个几边形( )
A. 八边形B. 九边形C. 十边形D. 十一边形
4.已知直线a//b，把Rt△ABC如图所示放置，点B在直线b上，∠ABC=90∘，∠A=30∘，若∠1=28∘，则∠2等于( )
A. 28∘
B. 32∘
C. 58∘
D. 60∘
5.如图，在△ABC中，∠ABC与∠ACB的角平分线交于点O，且∠A=70∘，则∠BOC的度数是( )
A. 110∘B. 125∘C. 140∘D. 145∘
6.如图，点B在线段AD上，△ABC≌△EBD，AB=2cm，BD=5cm，则CE的长度为( )
A. 2cm
B. 2.5cm
C. 3cm
D. 5cm
7.如图，小林从P点向西直走12米后，向左转，转动的角度为α，再走12米，如此重复，小林共走了108米回到点P，则α=( )
A. 30∘B. 40∘C. 80∘D. 108∘
8.如图，△ABC中，AD是中线，AB=5，AC=3，则AD的取值范围是( )
A. 3B. 2C. 1D. 09.如图所示，△ABC中，点D、E、F分别在三边上，E是AC的中点，AD、BE、CF交于一点G，BD=2DC，S△GEC=3，S△GDC=4，则△ABC的面积是( )
A. 25
B. .30
C. 35
D. 40
10.如图，Rt△ACB中，∠ACB=90∘，△ABC的角平分线AD、BE相交于点P，过P作PF⊥AD交BC的延长线于点F，交AC于点H，则以下结论：①∠APB=135∘；②PF=PA；③AH+BD=AB；④∠PFD=∠PAH，其中正确的个数是( )
A. 4
B. 3
C. 2
D. 1
二、填空题：本题共6小题，每小题3分，共18分。
11.若n边形的每一个外角都是40∘，则n的值为______.
12.将一把直尺和一个含30∘的三角板ABC按如图所示位置摆放，如果∠BDG=70∘，那么∠AFE的度数为______.
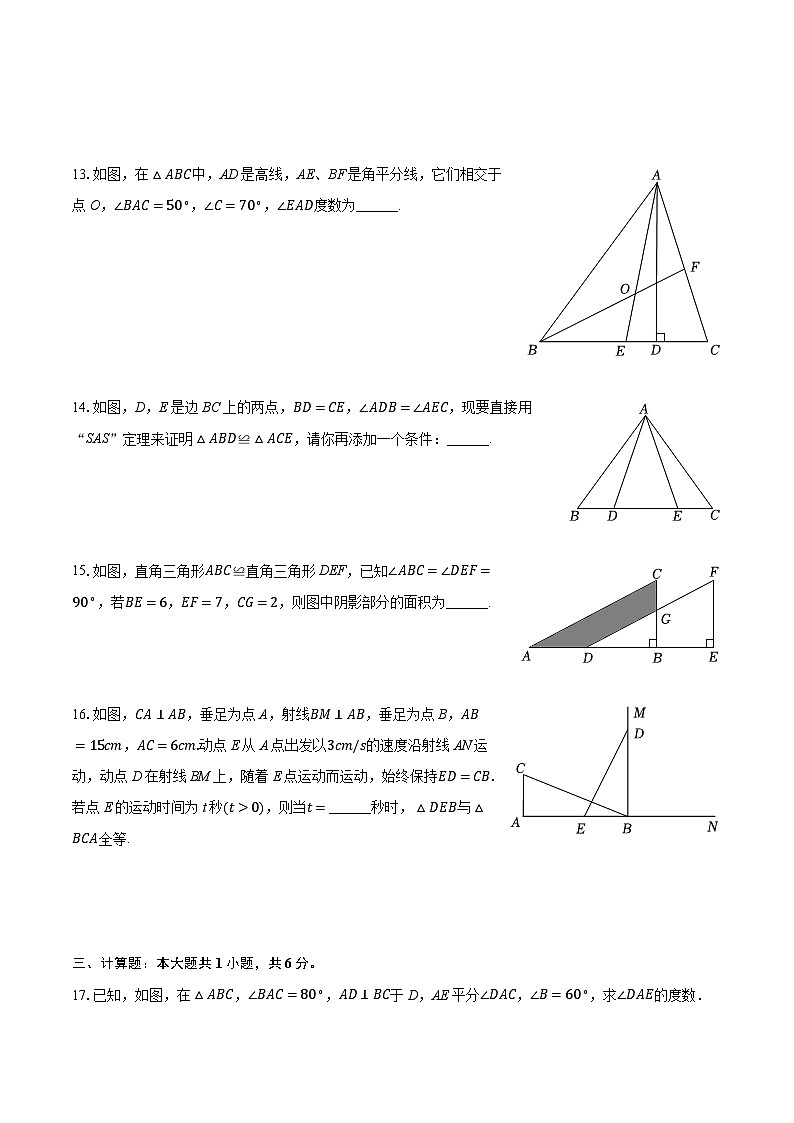
13.如图，在△ABC中，AD是高线，AE、BF是角平分线，它们相交于点O，∠BAC=50∘，∠C=70∘，∠EAD度数为______.
14.如图，D，E是边BC上的两点，BD=CE，∠ADB=∠AEC，现要直接用“SAS”定理来证明△ABD≌△ACE，请你再添加一个条件：______.
15.如图，直角三角形ABC≌直角三角形DEF，已知∠ABC=∠DEF=90∘，若BE=6，EF=7，CG=2，则图中阴影部分的面积为______.
16.如图，CA⊥AB，垂足为点A，射线BM⊥AB，垂足为点B，AB=15cm，AC=6cm.动点E从A点出发以3cm/s的速度沿射线AN运动，动点D在射线BM上，随着E点运动而运动，始终保持ED=CB.若点E的运动时间为t秒(t>0)，则当t=______秒时，△DEB与△BCA全等.
三、计算题：本大题共1小题，共6分。
17.已知，如图，在△ABC，∠BAC=80∘，AD⊥BC于D，AE平分∠DAC，∠B=60∘，求∠DAE的度数．
四、解答题：本题共7小题，共66分。解答应写出文字说明，证明过程或演算步骤。
18.(本小题6分)
如图所示的方格纸中，每个小正方形的边长均为1，点A，B，C均在小正方形的顶点上.
(1)画出△ABC的边BC上的高AD；
(2)画出△ABC的边AC上的中线BE；
(3)△ABE的面积为______.
19.(本小题8分)
已知一个多边形的边数为n，若这个多边形的每个内角都比与它相邻的外角的4倍多30∘，求这个多边形对角线的总条数.
20.(本小题8分)
如图，已知点A在BE上，DE=AB，DB=AC，BE=CB.
(1)试说明：DE//BC；
(2)若BC=12，DE=5，求AE的长.
21.(本小题10分)
如图，已知AB=AC，AD=AE，∠BAC=∠EAD，∠1=25∘，∠2=30∘.
(1)求证：△ABE≌△ACD；
(2)求∠3的度数.
22.(本小题10分)
如图，在△ABC中，BD、CE分别是△ABC的高，在BD上取一点P，使BP=AC，在CE的延长线上取一点Q，使CQ=AB，连接AQ与AP.
(1)求证：△ABP≌△QCA；
(2)判断AP与AQ的位置关系并证明你的结论.
23.(本小题12分)
【基本模型】：如图1，BO平分△ABC的内角∠ABC，CO平分△ABC的外角∠ACD，试证明：∠BOC=12∠A；
【变式应用】：
(1)如图2，直线PQ⊥MN，垂足为点O，作∠PON的角平分线OE，在OE上任取一点A，在ON上任取一点B，连接AB，作∠BAE的角平分线AC，AC的反向延长线与∠ABO的平分线相交于点F，请问：∠F的大小是否随着点A，B位置的变化而变化？若发生变化，请说明理由；若不发生变化，请求出其度数；
(2)在(1)的基础上，若FC//MN，则AB与OE有何位置关系？请说明理由．
24.(本小题12分)
【初步探索】
(1)如图1：在四边形ABCD中，AB=AD，∠B=∠ADC=90∘，E、F分别是BC、CD上的点，且EF=BE+FD，探究图中∠EAF与∠BAD之间的数量关系.
小王同学探究此问题的方法是：延长FD到点G，使DG=BE.连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是______；
【灵活运用】
(2)如图2，若在四边形ABCD中，AB=AD，∠B+∠D=180∘.E、F分别是BC、CD上的点，且EF=BE+FD，上述结论是否仍然成立，并说明理由；
【拓展延伸】
(3)如图3，已知在四边形ABCD中，∠ABC+∠ADC=180∘，AB=AD，若点E在CB的延长线上，点F在CD的延长线上，如图3所示，仍然满足EF=BE+FD，请写出∠EAF与∠DAB的数量关系，并给出证明过程.
答案和解析
1.【答案】C
【解析】解：∵三条线段的长分别是3，7，m，它们能构成三角形，
∴7-3∴4∴整数m的最大值是9.
故选：C.
根据三角形的三边关系确定第三边的取值范围，进而解答即可．
本题考查了三角形的三边关系，熟知三角形两边之和大于第三边，三角形的两边差小于第三边是解题的关键．
2.【答案】C
【解析】解：设∠1=x，则∠2=x，∠C=2x，
∵∠A+∠B+∠C=180∘，
∴x+x+2x=4x=180∘，
解得x=45∘，
∴∠C=2×45∘=90∘，
∴此三角形是直角三角形．
故选：C.
先设∠A=x，则∠B=x，∠C=2x，再根据三角形内角和定理列出方程，求出∠C的度数即可．
本题考查的是三角形内角和定理及直角三角形的判定定理，解答此题的关键是熟知三角形的内角和为180∘.
3.【答案】C
【解析】解：设它的边数为n，根据题意，得
(n-2)⋅180∘=1440∘，
解得：n=10.
故选：C.
利用多边形的内角和为(n-2)⋅180∘即可解决问题．
本题考查了多边形的内角和，利用多边形的内角和公式列方程即可解决问题．
4.【答案】C
【解析】解：∵∠3=∠1=28∘，∠4=∠3+∠A，
∴∠4=28∘+30∘=58∘.
∵a//b，
∴∠2=∠4=58∘.
故选：C.
先利用外角和内角的关系求出∠4，再利用平行线的性质求出∠2.
本题主要考查了平行线的性质，掌握“两直线平行，同位角相等“、”对顶角相等“、”三角形的外角等于与它不相邻的两个内角的和“是解决本题的关键．
5.【答案】B
【解析】【分析】
本题主要考查了三角形的内角和定理，以及三角形的角平分线的定义，难度适中．
在△ABC中，已知∠A即可得到∠ABC与∠ACB的和，而BO、CO是∠ABC，∠ACB的两条角平分线，即可求得∠OBC与∠OCB的度数，根据三角形的内角和定理即可求解．
【解答】
解：△ABC中，∠ABC+∠ACB=180∘-∠A=180∘-70∘=110∘，
∵BO、CO是∠ABC，∠ACB的两条角平分线．
∴∠OBC=12∠ABC，∠OCB=12∠ACB，
∴∠OBC+∠OCB=12(∠ABC+∠ACB)=55∘，
∴△OBC中，∠BOC=180∘-(∠OBC+∠OCB)=125∘.
故选：B.
6.【答案】C
【解析】解：∵△ABC≌△EBD，
∴BE=AB=2cm，BC=BD=5cm，
∴CE=BC-BE=5cm-2cm=3cm，
故选：C.
根据全等三角形的对应边相等，再利用线段和差即可求解．
此题考查了全等三角形的性质，解题的关键熟练掌握性质的应用．
7.【答案】B
【解析】解：设边数为n，根据题意，
n=108÷12=9，
则α=360∘÷9=40∘.
故选：B.
根据题意可知，小林走的是正多边形，先求出边数，然后再利用外角和等于360∘，除以边数即可求出α的值．
本题主要考查了多边形的外角和等于360∘，根据题意判断出所走路线是正多边形是解题的关键．
8.【答案】C
【解析】解：延长AD至点E，使DE=AD，
∵AD为BC边上的中线，
∴BD=CD，
在△ADC和△EDB中，
CD=BD∠ADC=∠EDBAD=DE，
∴△ADC≌△EDB(SAS)，
∴BE=AC=3，
∴5-3∴2∴1故选：C.
延长AD至点E，使DE=AD，利用SAS证明△ADC≌△EDB，得BE=AC=3，再利用三角形三边关系可得答案．
本题主要考查了全等三角形的判定与性质，三角形三边关系等知识，倍长中线是解题的关键．
9.【答案】B
【解析】解：BD=2DC，
∴S△ABD=2S△ACD，
∴S△ABC=3S△ACD，
∵E是AC的中点，
∴S△AGE=S△CGE，
又∵S△GEC=3，S△GDC=4，
∴S△ACD=S△AGE+S△CGE+S△CGD=3+3+4=10，
∴S△ABC=3S△ACD=3×10=30.
故选：B.
由于BD=2DC，那么结合三角形面积公式可得S△ABD=2S△ACD，而S△ABC=S△ABD+S△ACD，可得出S△ABC=3S△ACD，而E是AC中点，故有S△AGE=S△CGE，于是可求S△ACD，从而易求S△ABC.
本题考查了三角形的面积公式、三角形之间的面积加减计算．注意同底等高的三角形面积相等，面积相等、同高的三角形底相等．
10.【答案】A
【解析】解：在△ABC中，∠ACB=90∘，
∴∠BAC+∠ABC=90∘，
又∵AD、BE分别平分∠BAC、∠ABC，
∴∠BAD=12∠BAC，∠ABE=12∠ABC，
∴∠BAD+∠ABE=12(∠BAC+∠ABC)=45∘，
∴∠APB=135∘，故①正确；
∴∠BPD=45∘，
又∵PF⊥AD，
∴∠FPB=90∘+45∘=135∘，
∴∠APB=∠FPB，
又∵∠ABP=∠FBP，
在△ABP和△FBP中，
∠ABP=∠FBPBP=BP∠APB=∠FPB，
∴△ABP≌△FBP(ASA)，
∴∠BAP=∠BFP，AB=FB，PA=PF，故②正确；
∴∠PAH=∠BAP=∠BFP，故④正确；
在△APH和△FPD中，
∠APH=∠FPD∠PAH=∠PFBPA=PF，
∴△APH≌△FPD(AAS)，
∴AH=FD，
又∵AB=FB，
∴AB=FD+BD=AH+BD.故③正确；
故选：A.
根据三角形内角和定理以及角平分线定义判断①；根据全等三角形的判定和性质判断②③；根据角平分线的定义和全等三角形的性质判断④即可．
本题考查了角平分线的判定与性质，三角形全等的判定方法，三角形内角和定理．掌握相关性质是解题的关键．
11.【答案】9
【解析】解：∵n边形的每一个外角都是40∘，
∴此n边形是正n边形，
n=360∘÷40∘=9，
故答案为：9.
先判断出此多边形是正多边形，然后根据正多边形的边数等于360∘除以每一个外角的度数计算即可得解．
本题考查了多边形的内角与外角，熟练掌握正多边形的边数、每一个外角的度数、外角和三者之间的关系是解题的关键．
12.【答案】40∘
【解析】解：∵DG//EF，
∴∠BEF=∠BDG=70∘，
∵∠A=30∘，
∴∠AFE=70∘-30∘=40∘，
故答案为：40∘.
先根据平行线的性质求出∠BEF=70∘，然后根据三角形外角的性质即可求解．
本题考查了平行线的性质，三角形外角的性质，熟记平行线的性质，三角形外角的性质是解题的关键．
13.【答案】5∘
【解析】解：∵AD⊥BC，
∴∠ADC=90∘，
∵∠C=70∘，
∴∠DAC=180∘-90∘-70∘=20∘，
∵AE平分∠BAC，
∴∠CAE=12×50∘=25∘，
∴∠EAD=∠EAC-∠DAC=25∘-20∘=5∘.
故答案为：5∘.
因为AD是高，所以∠ADC=90∘，又因为∠C=70∘，求出∠DAC度数，根据∠EAD=∠EAC-∠DAC解答即可．
本题主要考查了利用角平分线的定义解决问题的能力，有利于培养同学们的发散思维能力．
14.【答案】AD=AE
【解析】解：当添加条件AD=AE时，可用定理“SAS”定理来证明△ABD≌△ACE，理由如下：
在△ABD和△ACE中，
BD=CE∠ADB=∠AECAD=AE，
∴△ABD≌△ACE(SAS)，
故答案为：AD=AE.
根据全等三角形的判定，定理“SAS”结合已知条件和图形即可得出答案．
本题主要考查了全等三角形的判定，准确识图，熟练掌握全等三角形的判定方法是解决问题的关键．
15.【答案】36
【解析】解：∵直角三角形ABC沿AB方向平移AD距离得到△DEF，
∴S△ABC=S△DEF，BC=EF=7，
∴GB=BC-CG=7-2=5，
∵S阴影部分+S△DBG=S△BDG+S梯形BEFG，
∴S阴影部分=S梯形BEFG=12×(5+7)×6=36.
故答案为：36.
利用平移的性质得到S△ABC=S△DEF，BC=EF=7，则GB=5，然后利用S阴影部分=S梯形BEFG进行计算．
本题考查了平移的性质：把一个图形整体沿某一直线方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同；新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点．连接各组对应点的线段平行(或共线)且相等．
16.【答案】3或7或10
【解析】解：∵CA⊥AB，BM⊥AB，
∠CAB=∠DBE=90∘，
∵ED=CB，
当E在线段AB上时，
若BE=AC，
∴Rt△DEB≌Rt△BCA(HL)，
∵AE=3tcm，
∴BE=AB-AE=(15-3t)cm，
∴15-3t=6，
∴t=3；
若BE=AB，
∴Rt△DEB≌Rt△CBA(HL)，
∴AE=0，
∴t=0(舍去)，
当E在线段AB延长线上时，
若BE=AC，
∴Rt△DEB≌Rt△BCA(HL)，
∵AE=3t=AB+BE=15+6=21(cm)，
∴t=7，
若BE=AB，
∴Rt△DEB≌Rt△CBA(HL)，
∵AE=3t=AB+BE=15+15=30(cm)，
∴t=10，
∴当t=3或7或10秒时，△DEB与△BCA全等．
故答案为：3或7或10.
分情况，当E在线段AB上，或当E在线段AB延长线上，由HL即可求解．
本题考查全等三角形的判定，关键是要分情况讨论．
17.【答案】解：∵AD⊥BC，
∴∠BDA=90∘，
∵∠B=60∘，
∴∠BAD=90∘-∠B=90∘-60∘=30∘
∵∠BAC=80∘，
∴∠DAC=∠BAC-∠BAD=80∘-30∘=50∘
∵AE平分∠DAC，
∴∠DAE=12∠DAC=12×50∘=25∘.
【解析】首先根据三角形内角和定理求得∠BAD，根据和差关系和角平分线的定义求得∠DAE.
本题考查三角形内角和定理、角平分线的定义等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．
18.【答案】6
【解析】解：(1)如图，AD即为所求．
(2)如图，BE即为所求．
(3)由题意得，△ABE的面积为12S△ABC=12×12×4×6=6.
故答案为：6.
(1)根据三角形的高的定义画图即可．
(2)根据三角形的中线的定义画图即可．
(3)由题意可得，△ABE的面积为12S△ABC，进而可得答案．
本题考查作图-应用与设计作图、三角形的角平分线、中线和高、三角形的面积，熟练掌握三角形的中线和高的定义是解答本题的关键．
19.【答案】解：设这个多边形的每个外角为x∘，则每个内角为(4x+30)∘，依题意得，
4x+30+x=180，
解得x=30，
∴n=360∘÷30∘=12，
∴这个多边形对角线的总条数=(12-3)×122=54，
答：这个多边形对角线的总条数为54.
【解析】根据题意，求出每个外角的度数，再用外角和360∘除以外角的度数得到边数，代入多边形对角线的总条数计算公式n(n-3)2求解即可．
本题考查了求多边形内角和与外角和的综合，求多边形对角线的总条数，掌握多边形对角线的总条数计算公式是解题的关键．
20.【答案】(1)证明：在△BDE和△CBA中，
BD=CBDE=BABE=CA，
∴△BDE≌△CAB(SSS)，
∴∠EBC=∠E，
∴DE//BC；
(2)解：∵△BDE≌△CAB，BC=12，DE=5，
∴DE=AB=5，BE=BC=12，
∴AE=BE-AB=BE-DE=12-5=7.
【解析】(1)根据全等三角形的对应角相等得到∠E=∠EBC，然后根据内错角相等，两直线平行得到结论即可；
(2)根据全等三角形的对应边相等得到BE=BC=12，DE=AB，然后利用线段的和差即可得到结果．
本题考查全等三角形的判定和性质，平行线的判定，掌握全等三角形的性质是解题的关键．
21.【答案】(1)证明：∵BAC=∠BAE+∠CAE，∠DAE=∠1+∠CAE，∠BAC=∠DAE，
∴∠1=∠BAE，
在△ABE和△ACD中
AB=AC∠1=∠BAEAD=AE，
∴△ABE≌△ACD(SAS)；
(2)解：∵△ABE≌△ACD，
∴∠2=∠ABD=30∘，
∴∠3=∠BAE+∠ABD=∠1+∠ABD=25∘+30∘=55∘.
【解析】根据∠BAC=∠DAE，通过角的计算即可得出∠1=∠BAE，结合AB=AC、AD=AE即可证出△BAE≌△CAD(SAS)，进而即可得出∠ABD=∠2=30∘.再根据外角的性质即可得出∠3的度数．
此题考查全等三角形的判定与性质，解题关键在于掌握全等三角形的判定定理．
22.【答案】解：(1)∵∠ADB=∠AEC=90∘，
∴∠ABP+∠BAD=90∘，∠ACE+∠CAE=90∘，
∴∠ABP=∠QCA，
在△ABP和△QCA中，
BP=AC∠ABP=∠QCACQ=AB，
∴△ABP≌△QCA(SAS)；
(2)AP⊥AQ，理由为：
由(1)得∠BAP=∠Q，∠Q+∠QAE=90∘，
∴∠BAP+∠QAE=90∘，
则AQ⊥AP.
【解析】(1)由同角的余角相等得到一对角相等，再由已知两对边相等，利用SAS即可得证；
(2)AP与AQ垂直，理由为：根据(1)的结论得到∠BAP=∠Q，∠Q+∠QAE=90∘，利用等角的余角相等即可得证．
此题考查了全等三角形的判定与性质，熟练掌握全等三角形的判定与性质是解本题的关键．
23.【答案】【基本模型】
证明：∵∠OCD=∠OBC+∠BOC，∠ACD=∠ABC+∠A，
∴∠BOC=∠OCD-∠OBC，∠A=∠ACD-∠ABC，
又∵CO平分∠ACD，BO平分∠ABC，
∴∠OCD=12∠ACD，∠OBC=12∠ABC，
∴∠OCD-∠OBC=12(∠ACD-∠ABC)，
∴∠BOC=12∠A；
【变式应用】
解：(1)∠F的大小不变；理由如下：
∵PQ⊥MN，
∴∠PON=90∘，
∵OE是∠PON的平分线，
∴∠AOB=12∠PON=45∘，
∵∠BAC=∠ABF+∠F，∠BAE=∠ABO+∠AOB，
∴∠F=∠BAC-∠ABF，∠AOB=∠BAE-∠ABO，
∵AC、BF分别平分∠BAE、∠ABO，
∴∠BAC=12∠BAE，∠ABF=12∠ABO，
∴∠BAC-∠ABF=12(∠BAE-∠ABO)，
∴∠F=12∠AOB=22.5∘；
(2)AB⊥OE，理由如下：
∵FC//MN，
∴∠FBO=∠F=22.5∘，
∵BF平分∠ABO，
∴∠ABO=2∠FBO=45∘，
∴∠OAB=180∘-∠AOB-∠ABO=90∘，
∴AB⊥OE.
【解析】【基本模型】由三角形的外角性质得∠BOC=∠OCD-∠OBC，∠A=∠ACD-∠ABC，由角平分线定义得∠OCD=12∠ACD，∠OBC=12∠ABC，进而得出结论；
【变式应用】(1)由角平分线定义得∠AOB=12∠PON=45∘，由三角形的外角性质得∠F=∠BAC-∠ABF，∠AOB=∠BAE-∠ABO，由角平分线定义得∠BAC=12∠BAE，∠ABF=12∠ABO，则∠BAC-∠ABF=12(∠BAE-∠ABO)，即可得出结论；
(2)由平行线的性质得∠FBO=∠F=22.5∘，证出∠ABO=2∠FBO=45∘，由三角形内角和定理即可得出结论．
本题考查了平行线的性质、角平分线定义、三角形的外角性质以及三角形内角和定理等知识；熟练掌握平行线的性质和三角形的外角性质是解题的关键．
24.【答案】∠BAE+∠FAD=∠EAF
【解析】解：(1)∠BAE+∠FAD=∠EAF.理由：
如图1，延长FD到点G，使DG=BE，连接AG，
在△ABE和△ADG中，
AB=AD∠B=∠ADG=90∘BE=DG，
∴△ABE≌△ADG(SAS)，
∴∠BAE=∠DAG，AE=AG，
∵EF=BE+DF，DG=BE，
∴EF=BE+DF=DG+DF=GF，
∵AF=AF，
∴△AEF≌△AGF(SSS)，
∴∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF.
故答案为：∠BAE+∠FAD=∠EAF；
(2)结论仍成立，理由：
如图2，延长FD到点G，使DG=BE，连接AG，
∵∠B+∠ADF=180∘，∠ADG+∠ADF=180∘，
∴∠B=∠ADG，
又∵AB=AD，
∴△ABE≌△ADG(SAS)，
∴∠BAE=∠DAG，AE=AG，
∵EF=BE+FD=DG+FD=GF，AF=AF，
∴△AEF≌△AGF(SSS)，
∴∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF；
(3)∠EAF=180∘-12∠DAB.
证明：如图3，在DC延长线上取一点G，使得DG=BE，连接AG，
∵∠ABC+∠ADC=180∘，∠ABC+∠ABE=180∘，
∴∠ADC=∠ABE，
又∵AB=AD，
∴△ADG≌△ABE(SAS)，
∴AG=AE，∠DAG=∠BAE，
∵EF=BE+FD=DG+FD=GF，AF=AF，
∴△AEF≌△AGF(SSS)，
∴∠FAE=∠FAG，
∵∠FAE+∠FAG+∠GAE=360∘，
∴2∠FAE+(∠GAB+∠BAE)=360∘，
∴2∠FAE+(∠GAB+∠DAG)=360∘，
即2∠FAE+∠DAB=360∘，
∴∠EAF=180∘-12∠DAB.
(1)延长FD到点G，使DG=BE，连接AG，可判定△ABE≌△ADG，进而得出∠BAE=∠DAG，AE=AG，再判定△AEF≌△AGF，可得出∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF，据此得出结论；
(2)延长FD到点G，使DG=BE，连接AG，先判定△ABE≌△ADG，进而得出∠BAE=∠DAG，AE=AG，再判定△AEF≌△AGF，可得出∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF；
(3)在DC延长线上取一点G，使得DG=BE，连接AG，先判定△ADG≌△ABE，再判定△AEF≌△AGF，得出∠FAE=∠FAG，最后根据∠FAE+∠FAG+∠GAE=360∘，推导得到2∠FAE+∠DAB=360∘，即可得出结论．
本题属于四边形综合题，主要考查了全等三角形的判定以及全等三角形的性质的综合应用，解决问题的关键是作辅助线构造全等三角形，根据全等三角形的对应角相等进行推导变形．解题时注意：同角的补角相等．