河北省衡水中学2024−2025学年高二上学期第一次综合素养测评 数学试题（含解析）

这是一份河北省衡水中学2024−2025学年高二上学期第一次综合素养测评 数学试题（含解析），共19页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
一、单选题（本大题共8小题）
1．已知集合，，若，则（ ）
A．B．
C．D．
2．已知某学校参加学科节数学竞赛决赛的8人的成绩（单位：分）为：72，78，80，81，83，86，88，90，则这组数据的第75百分位数是（ ）
A．86B．87C．88D．90
3．将除颜色外完全相同的2个红球和1个白球随机放入2个不同的盒子中，每个盒子中至少放入1个球，则2个红球分别放入不同盒子中的概率为（ ）
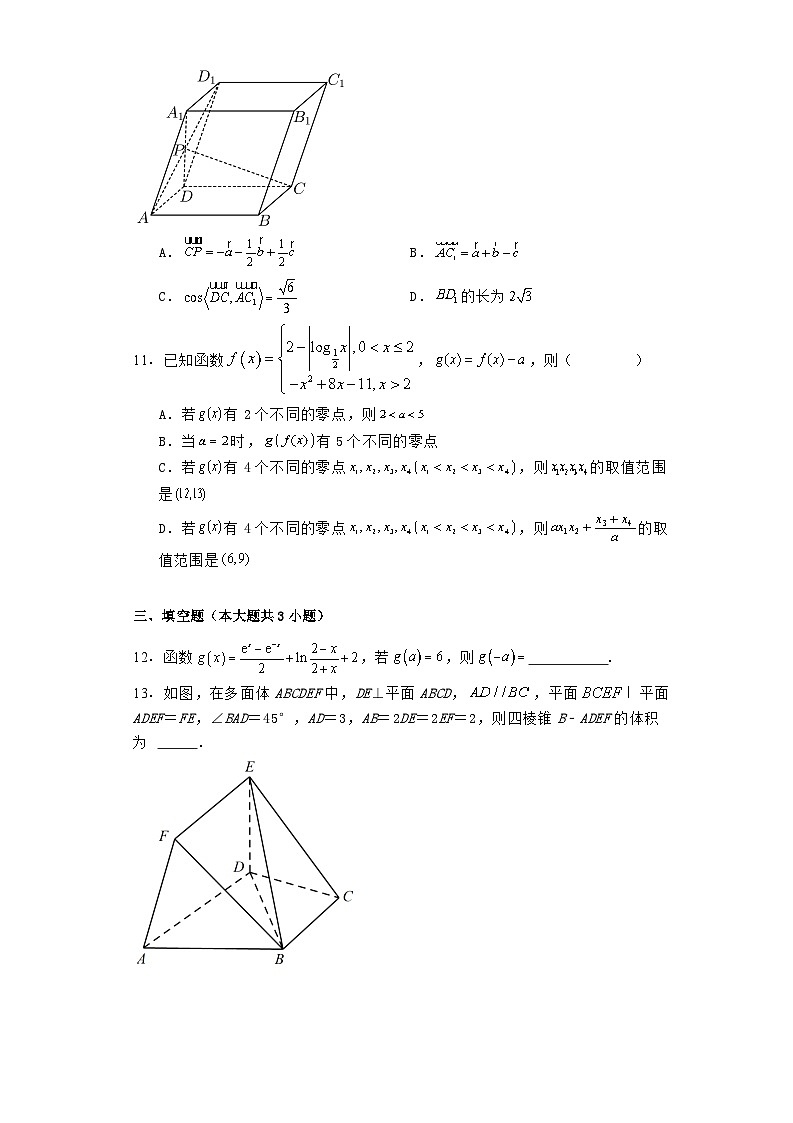
A．B．C．D．
4．在正方体中，若，P，Q分别为AC，的中点，则直线PQ与AO所成角的大小为（ ）
A．B．C．D．
5．已知向量满足，且在上的投影向量为，则向量与向量的夹角为（ ）
A．B．C．D．
6．已知非负实数满足，则的最小值为（ ）
A．B．2C．D．
7．为了发展旅游业，方便游客观赏湖面盛开的睡莲和湖里游动的锦鲤，唐山南湖公园拟修建观景栈桥．规划如图所示，为规划区域，面积为万平方米，，，，是四条观景木栈桥，其中，，，为观景玻璃栈桥，则的最小值（单位：百米）为（ ）
A．B．4C．D．
8．如图，四棱锥是棱长均为2的正四棱锥，三棱锥是正四面体，G为的中点，则下列结论错误的是（ ）
A．点共面B．平面平面
C．D．平面ACD
二、多选题（本大题共3小题）
9．若数据的平均数为3，方差为4，则下列说法正确的是（ ）
A．数据的平均数为13
B．数据的方差为12
C．
D．
10．如图，在平行六面体中，以顶点为端点的三条棱长都是2，且它们彼此的夹角都是为与的交点，若，则下列正确的是（ ）
A．B．
C．D．的长为
11．已知函数，，则（ ）
A．若有2个不同的零点，则
B．当时，有5个不同的零点
C．若有4个不同的零点，则的取值范围是
D．若有4个不同的零点，则的取值范围是
三、填空题（本大题共3小题）
12．函数，若，则 .
13．如图，在多面体ABCDEF中，DE⊥平面ABCD，，平面平面ADEF＝FE，∠BAD＝45°，AD＝3，AB＝2DE＝2EF＝2，则四棱锥B﹣ADEF的体积为 ．
14．将函数的图象向左平移个单位长度得到函数的图象，若，则的最小值为 ．
四、解答题（本大题共5小题）
15．某射击训练队制订了如下考核方案：每一次射击中10环、中8环或9环、中6环或7环、其他情况，分别评定为A，B，C，D四个等级，各等级依次奖励2分、奖励0分、罚2分、罚4分．假设评定为等级为A，B，C的概率分别是，，．
(1)若某射击选手射击一次，求其被罚分的概率；
(2)若某射击选手射击两次，且两次射击互不影响，求这两次射击得分之和为0分的概率．
16．的内角A，B，C的对边分别为a，b，c，已知，．
(1)求A；
(2)若点D在BC边上，AD平分BAC，且，求的周长．
17．如图，等腰梯形中，，，，为的中点，将沿折起，得到四棱锥，为的中点.
(1)线段上是否存在点，使平面？
(2)证明：为直角三角形；
(3)当四棱锥的体积最大时，求三棱锥的体积.
18．已知函数，对，有.
(1)求的值及的单调递增区间；
(2)若，，求；
(3)将函数图象上的所有点，向右平移个单位后，再将所得图象上的所有点，纵坐标不变，横坐标变为原来的倍，得到函数的图象.若，，求实数的取值范围.
19．类比思想在数学中极为重要，例如类比于二维平面内的余弦定理，有三维空间中的三面角余弦定理：如图1，由射线，，构成的三面角，记，，，二面角的大小为，则．如图2，四棱柱中，为菱形，，，，且点在底面内的射影为的中点．
(1)求的值；
(2)直线与平面内任意一条直线夹角为，证明：；
(3)过点作平面，使平面平面，且与直线相交于点，若，求值．
参考答案
1．【答案】D
【分析】分，讨论，利用可得答案.
【详解】因为，所以，
①时，，解得；
②时，则有，解得.
综上，m的取值范围是.
故选D.
2．【答案】B
【分析】根据样本数据百分位数的定义求解即可.
【详解】将数据从小到大排序得，
因为，
所以第75百分位数是．
故选B．
3．【答案】A
【分析】分析求出所有的基本事件，然后由古典概型的计算公式求解即可.
【详解】将除颜色外完全相同的2个红球和1个白球随机放入2个不同的盒子中，
每个盒子中至少放入1个球，则基本事件有：（红1，白红2），（白，红1红2），（红2，白红1），
则2个红球分别放入不同盒子中包含了（红1，白红2），（红2，白红1），
所以由古典概型的公式得概率为：.
故选A.
4．【答案】D
【分析】利用，将直线PQ与AO所成角转化成两相交直线与AO所成的角，通过计算证明，推理得到即得.
【详解】
如图，连接,由已知得，，则直线PQ与AO所成的角即为直线与AO所成的角.
由可得,则与AO相交.
在和中，，，
所以，所以，
所以，
所以，即直线PQ与AO所成角的大小为．
故选D.
5．【答案】C
【分析】先利用投影向量求出数量积，利用夹角公式可得答案.
【详解】依题意，在上的投影向量为，则，
于是，而，则，
所以向量与向量的夹角为.
故选C.
6．【答案】B
【分析】依题意可得且，利用乘“1”法及基本不等式计算可得.
【详解】因为非负实数满足，
显然，则，所以，
则，
当且仅当，即，时取等号，
所以的最小值为.
故选B.
7．【答案】C
【分析】根据题意，设的边，，利用三角形的面积公式求出，然后以向量，为基底，表示出向量，利用向量模的公式与平面向量数量积的运算性质，推导出，再根据基本不等式求出的最小值，进而得出的最小值．
【详解】中，设，，由，，
可得，即，所以．
因为，所以，
由，得，即，整理得，
因为，
所以，
而，所以，当且仅当时，即，时，等号成立．
因此，当，时，的最小值为，即的最小值为百米．
故选C．
8．【答案】D
【分析】A.由题意转化为证明平面和平面，即可证明；B.根据面面平行的判断定理转化为证明平面和平面，即可证明；C.由A选项的证明可证明线线垂直；D.利用反证法，说明不成立.
【详解】选项A：如图，取中点，连接,,,，
因为是正四棱锥，是正四面体，为的中点，
所以，,，
因为，平面，所以平面，
因为，平面，所以平面，
所以四点共面，
由题意知，，所以四边形是平行四边形，
所以，因为，所以，所以四点共面，故A说法正确；
选项B：由选项A知，又平面，平面，所以平面，
因为，且平面，平面，所以平面，
又平面，平面，且，所以平面平面，故B说法正确；
C选项：由选项A可得平面，又平面，所以，故C说法正确；
D选项：假设平面，因为平面，则，
由选项A知四边形是平行四边形，所以四边形是菱形，
与，矛盾，故D说法错误.
故选D.
9．【答案】ACD
【分析】由题意可得，，利用平均数的性质可得A；利用方差的性质计算可得B：由即可得C；结合方差与平均数计算即可得D.
【详解】依题意，，，
对A：，故A正确；
对B：依题意，，
所以数据的方差为：
，故B错误；
对C：，故C正确;
对D：由，解得，故D正确.
故选ACD.
10．【答案】AC
【分析】A，B选项考查的是空间向量基本定理的应用，以，，为基底表示，就可以得到结论；C选项考查利用空间向量数量积求向量夹角的余弦，先用基底表示和，再求它们的数量积和模，利用可判断C是否正确；对D选项，先用基底表示，再结合可求的长.
【详解】
，故A正确.
.故B错误.
又，.
，；
，
.
.
.故C正确.
，.故D错误.
故选AC.
11．【答案】BCD
【分析】作出的图象，由有2个不同的零点，结合图象，可判定A错误；由，令，得到，求得，结合图象，可判定B正确；由对数的运算性质，求得，结合二次函数的对称性得到，进而判定C正确；由，结合对勾函数的性质，可判定D正确．
【详解】由函数，可得，
作出的图象，如图所示．
对于A中，由，可得，若有2个不同的零点，
结合图象知或，故A错误；
对于B中，当时，由，可得，
令，则有，可得，
结合图象知，有3个不等实根，有2个不等实根，没有实根，
所以有5个不同的零点，故B正确；
对于C中，若有4个不同的零点，
则，且，则，
由二次函数的对称性得，则，
结合B知，所以，所以的取值范围为，故C正确；
对于D中，由，其中，
由对勾函数的性质，可得在上为单调递减函数，可得，
所以的取值范围为，故D正确．
故选BCD．
12．【答案】
【分析】利用和的关系求解即可.
【详解】，
，
.
故答案为：
13．【答案】
【分析】由已知证明，可得，利用等体积法求的体积，进一步可得四棱锥的体积.
【详解】因为，平面，平面，
所以平面，
因为平面，平面平面，
所以，
所以，
因为，
所以，，
所以，即，
因为平面，
所以是三棱锥的高，
因为，
所以，
所以，
故答案为：.
14．【答案】
【分析】利用平移变化得到的解析式，再根据知，，代入的解析式即可求出的取值范围，再结合，求出的最小值.
【详解】将函数的图象向左平移个单位长度得到函数，
又，则，
，或
即，或，
又，的最小值为.
故答案为：.
15．【答案】(1)；
(2).
【分析】(1)设事件分别表示“被评为等级A，B，C，D”.由题意，事件两两互斥，然后利用互斥事件的概率加法公求解即可；
(2)设事件，且事件互斥，然后分别求出对应的概率，再利用互斥事件的概率加法公求解即可.
【详解】(1)设事件A，B，C，D分别表示“被评定为等级A，B，C，D”．
由题意得，事件A，B，C，D两两互斥，所以．
又因为被罚分，所以．
因此其被罚分的概率为；
(2)设事件，，，表示“第i次被评定为等级A，B，C，D”，，2．
则“两次射击得分之和为0分”为事件，且事件，，互斥，
，
，
所以两次射击得分之和为0分的概率
.
16．【答案】(1)；
(2).
【分析】(1)利用正弦定理边化角，再利用三角恒等变换求出角即可；
(2)利用角平分线分三角形面积等于两个小三角形面积之和得出等式，再用余弦定理联立求解周长即可.
【详解】(1)由正弦定理得，
在中，，
化简为，又，
，又
；
(2)依题意得，
即，
由余弦定理得，
，解得
的周长为.
17．【答案】(1)存在，为的中点，理由见解析；
(2)证明见解析；
(3).
【分析】(1)为的中点，取中点，连接，证明，再利用线面平行的判定推理即可.
(2)取的中点，连接，，，由线面垂直的判定证得面即可作答.
(3)利用(2)中信息确定在体积最大时，求出点到平面距离，再结合锥体体积公式计算作答.
【详解】(1)存在，为的中点，
如图，取中点，连接，而为的中点，则，，
在等腰梯形中，，又为的中点，
于是得，，即有四边形为平行四边形，则，
又平面，平面，所以平面.
(2)取的中点，连接，，，如图，
由(1)知，，，即为平行四边形，则，，
有，为正三角形，则有，，
在原等腰梯形中，为正三角形，则，
于是得，而，即有为正三角形，，则，
又，平面，则平面，而平面，因此，
所以为直角三角形.
(3)由(2)知，是边长为4的菱形，且，即的面积是定值，
当四棱锥的体积最大时，即有点到平面距离最大，有直线平面，
则的高即为四棱锥的高，又为的中点，则到平面的距离，
又，于是得，
所以三棱锥的体积为4.
18．【答案】(1)，单调递增区间为（）；
(2)；
(3)或.
【分析】(1)利用三角函数恒等变换得到，根据得到方程，求出，得到函数解析式，整体法得到函数单调性；
(2)根据得到，凑角法，结合正弦和角公式得到答案；
(3)根据伸缩和平移变换得到，令，故，令，从而得到，因为，所以当时，，所以，解出答案.
【详解】(1)，
因为对，有，可得当时，取得最值，
所以，，
可得，，又，
所以，
所以，
由，，可得，，
所以的单调递增区间为（）.
(2)由，，，
可得，，
所以，
所以.
(3)将函数图象上的所有点，向右平移个单位后得到
函数的图象，进而可得，
令，
只需，
令，
因为，所以，
所以，
因为，可得，
所以，
因为，所以当时，，
所以，即，解得或.
所以实数的取值范围为或.
19．【答案】(1)
(2)证明见解析
(3)
【分析】（1）连接，即可证明平面平面，即二面角的大小为，求出，再由所给三面角余弦定理计算可得；
（2）依题意可得，设平面内任一条直线为，分过点与不过点两种情况，当过点，记与的夹角为（），则，结合余弦函数的性质即可得证；
（3）连接，，首先证明平面平面，从而得到平面平面，再由面面平行的性质得到，从而得到，即可得解.
【详解】（1）连接，由已知得平面，，
又平面，所以平面平面，
所以二面角的大小为，因为为菱形，，
所以，又，所以，
在中，，
由三面角余弦定理可得
.
（2）依题意可得，设平面内任一条直线为，
若过点时，记与的夹角为（），
则，因为，
所以，
又，所以；
若不过点时，过点作使得，记与的夹角为（），
则，因为，
所以，
又，所以；
综上可得.
（3）连接，，
因为，平面，平面，所以平面，
同理可证平面，
又，平面，
所以平面平面，
因为平面平面，
所以平面平面，
又平面平面，又平面平面，
所以，又即，
所以四边形为平行四边形，
所以，显然在的延长线上，
因为，所以，
所以，即.