初中数学人教版（2024）九年级下册27.3 位似教学课件ppt

这是一份初中数学人教版（2024）九年级下册27.3 位似教学课件ppt，共23页。PPT课件主要包含了学习目标，新课引入，新知学习，课堂小结，是位似图形，不是位似图形，画位似图形，CC′等内容，欢迎下载使用。
1. 掌握位似图形的概念、性质和画法. 2. 掌握位似与相似的联系与区别.
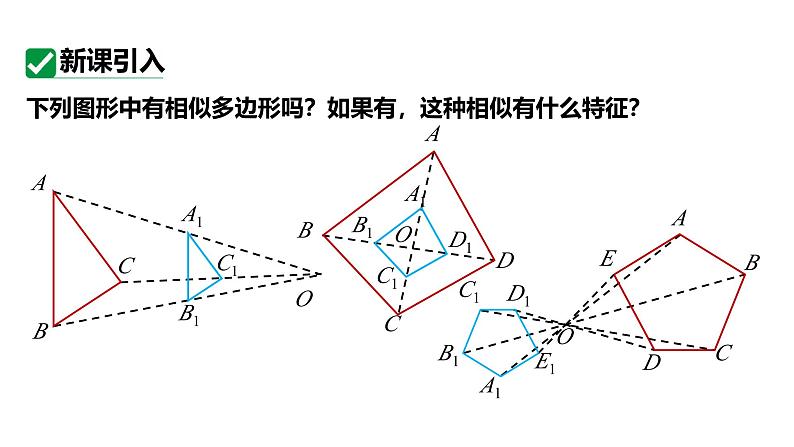
下列图形中有相似多边形吗？如果有，这种相似有什么特征？
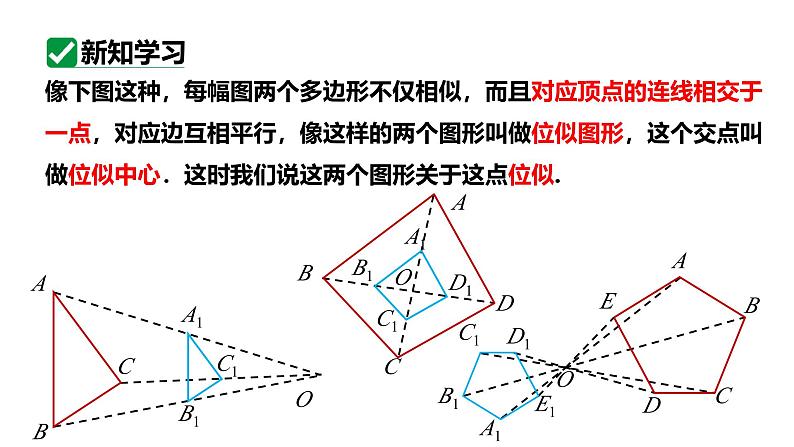
像下图这种，每幅图两个多边形不仅相似，而且对应顶点的连线相交于一点，对应边互相平行，像这样的两个图形叫做位似图形，这个交点叫做位似中心．这时我们说这两个图形关于这点位似.
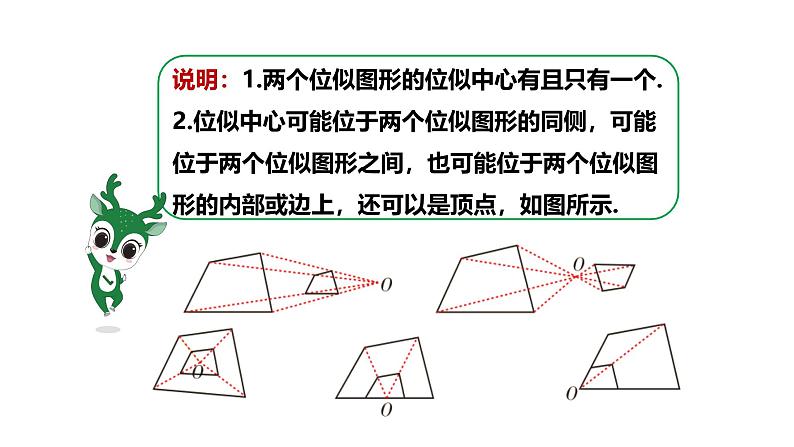
说明：1.两个位似图形的位似中心有且只有一个. 2.位似中心可能位于两个位似图形的同侧，可能位于两个位似图形之间，也可能位于两个位似图形的内部或边上，还可以是顶点，如图所示.
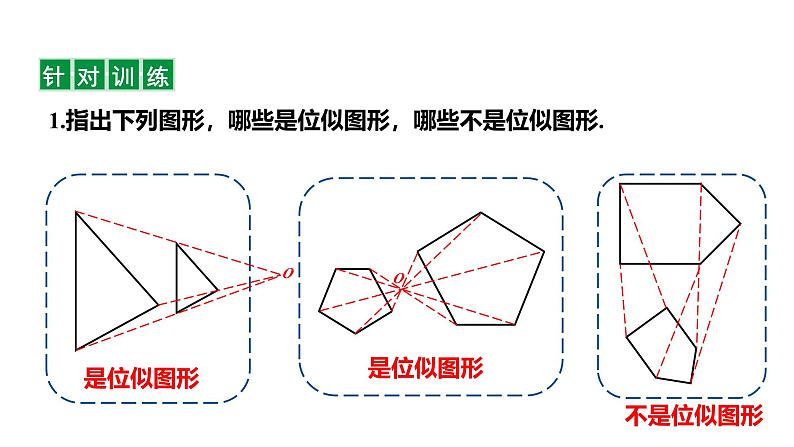
1.指出下列图形，哪些是位似图形，哪些不是位似图形.
怎样判断一组图形是否为位似图形？
对于两个多边形，如果它们的对应顶点的连线相交于一点，并且这点与对应顶点所连线段成比例，那么这两个多边形就是位似多边形。
总结：1.位似图形是一种特殊的相似图形，它具有相似图形的所有性质，即对应角相等，对应边的比相等.2.位似图形上任意一对对应点到位似中心的距离之比等于相似比.（位似图形的相似比也叫做位似比）
例 把四边形 ABCD 缩小到原来的 .
(1) 在四边形外任选一点 O (如图)；
例把四边形 ABCD 缩小到原来的 .
(2) 连接OA、OB、OC、OD，分别在线段 OA、OB、OC、OD 上取点 A' 、B' 、C' 、D' ，使得 ；
(3) 顺次连接点 A' 、B' 、C' 、D' ，所得四边形 A'B'C'D' 就是所要求的图形．
对于上面的问题，还有其他方法吗？如果在四边形外任选一个点 O，分别在 OA、OB、OC、OD的反向延长线上取 A′ 、B′ 、C′、D′，使得 呢?
如果点 O 取在四边形 ABCD 内部呢？
5. 如图，以 O 为位似中心，将 △ABC 放大为原来的2 倍．
解：①作射线 OA、OB、OC；
②分别在 OA、OB、OC 上取点 A'、B'、C'，使得
③顺次连接 A'、B'、C' 就是所要求作的图形.
① 确定位似中心；② 分别连接并延长位似中心和能代表原图的关键点；③ 根据相似比，确定能代表所作的位似图形的关键点；④ 顺次连接上述各点，得到放大或缩小的图形.
画位似图形的一般步骤：
1.如图，△ABC. 根据要求作△A'B'C'，使△A'B'C'∽△ABC，且相似比为 1 : 5.(1) 位似中心 O 在 △ABC 的一条边 AB 上；
在AB上任取一点 O 位置如图所示.根据相似比可确定 A′、B′、C′ 的位置.
2.如图，△ABC. 根据要求作△A'B'C'，使△A'B'C'∽△ABC，且相似比为 1 : 5.(2) 以点 C 为位似中心.
1.△ABC 与△A′B′C′ 是位似图形，且△ABC 与△A′B′C′ 的位似比是 1 : 2，已知 △ABC 的面积是 3，则 △A′B′C′ 的面积是(　　)　　　　　　　　　　　　　　　　　 A．3B．6C．9D．12
2.如图，在平面直角坐标系中，正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，且相似比为1 : 3，点A，B，E在x轴上，若正方形BEFG的边长为6，则C点坐标为（   ）．A．(3,2) B．(3,1)C．(2,2)C．(2,2)D．(4,2)
解析：∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，且相似比为1 : 3∴AD=BC=2，∵AD//BG，∴△OAD∽△ OBG，∴ 即OA=1，∴OB=3，∴C点坐标为(3,2)．
1.什么是位似图形？ 两个相似多边形，如果它们对应顶点所在的直线相交于一点，我们就把这样的两个图形叫做位似图形，这个交点叫做位似中心．2.位似图形有哪些性质？ 位似图形是一种特殊的相似图形，它具有相似图形的所有性质，即对应角相等，对应边的比相等. 位似图形上任意一对对应点到位似中心的距离之比等于相似比.（位似图形的相似比也叫做位似比）