高中数学人教版第一册下册函数 的图象图片ppt课件

这是一份高中数学人教版第一册下册函数 的图象图片ppt课件，共15页。PPT课件主要包含了建系画图，等分圆，找横坐标，连线得图，找纵坐标，左右平移，描点法，几何法，五点法，列表→描点→连线等内容，欢迎下载使用。

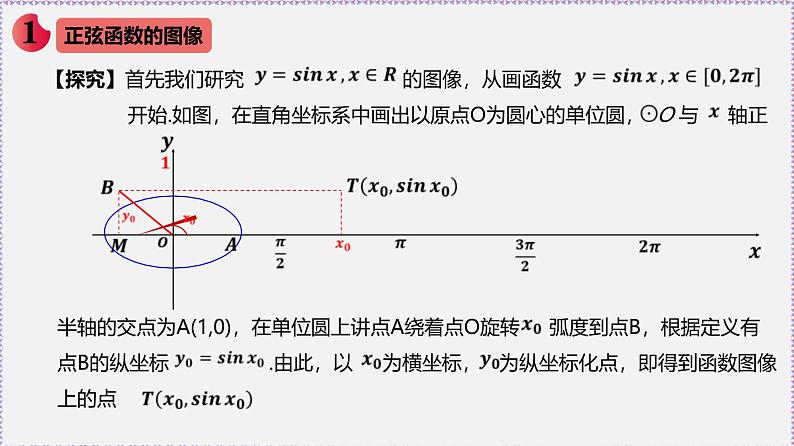
【探究】首先我们研究 的图像，从画函数 开始.如图，在直角坐标系中画出以原点O为圆心的单位圆， O 与 轴正
半轴的交点为A(1,0)，在单位圆上讲点A绕着点O旋转 弧度到点B，根据定义有点B的纵坐标 .由此，以 为横坐标， 为纵坐标化点，即得到函数图像上的点
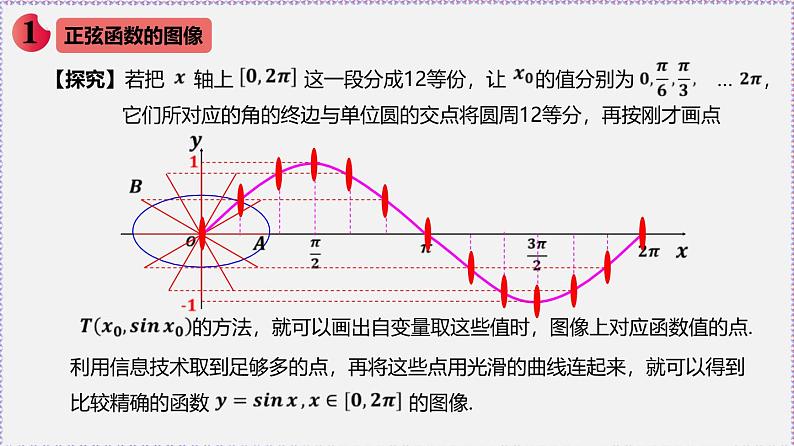
【探究】若把 轴上 这一段分成12等份，让 的值分别为 … ， 它们所对应的角的终边与单位圆的交点将圆周12等分，再按刚才画点
的方法，就可以画出自变量取这些值时，图像上对应函数值的点.
利用信息技术取到足够多的点，再将这些点用光滑的曲线连起来，就可以得到比较精确的函数 的图像.
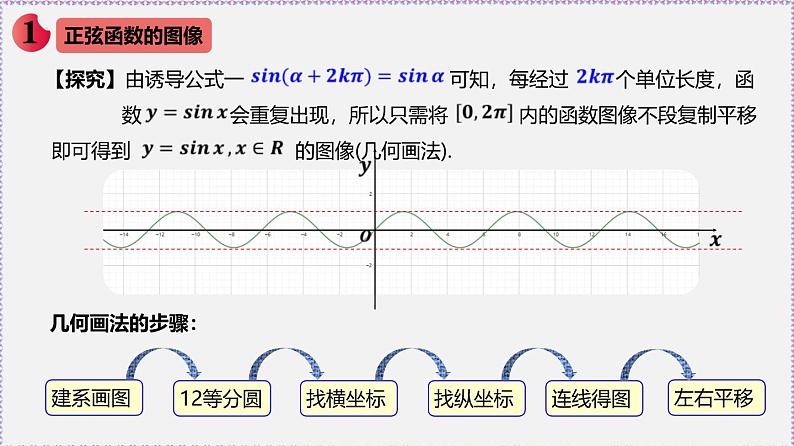
【探究】由诱导公式一 可知，每经过 个单位长度，函 数 会重复出现，所以只需将 内的函数图像不段复制平移 即可得到 的图像(几何画法).
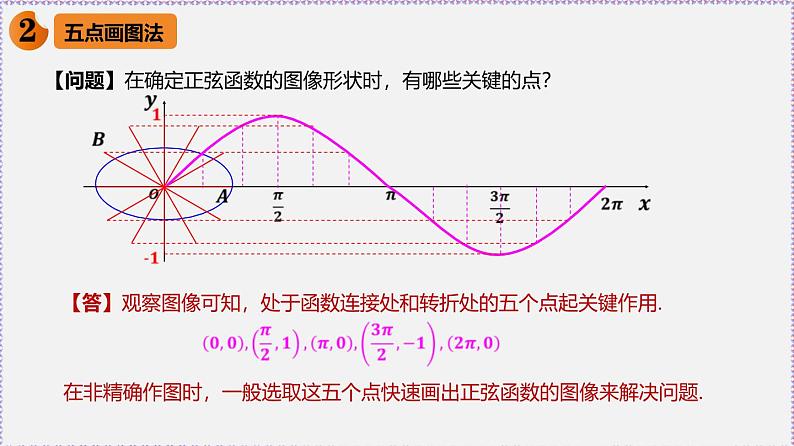
【问题】在确定正弦函数的图像形状时，有哪些关键的点？
【答】观察图像可知，处于函数连接处和转折处的五个点起关键作用.
在非精确作图时，一般选取这五个点快速画出正弦函数的图像来解决问题.
利用单位圆在[0，2π]上取足够多的点连线
描最高点最低点,图像和坐标轴的三个交点
只能取近似值，误差较大
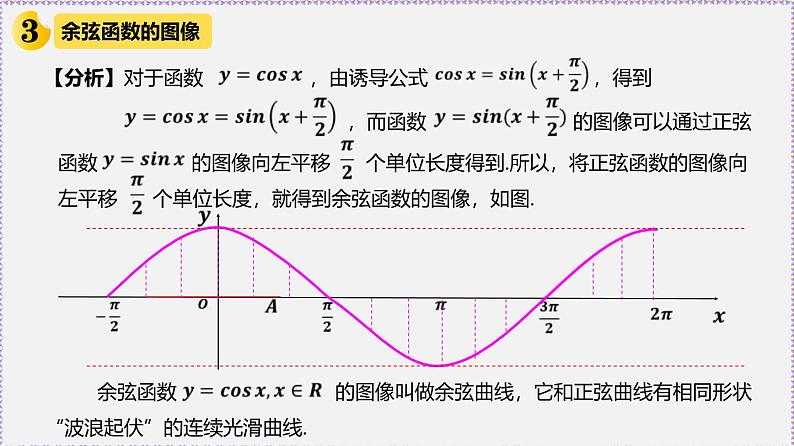
【分析】对于函数 ，由诱导公式 ，得到
，而函数 的图像可以通过正弦
函数 的图像向左平移 个单位长度得到.所以，将正弦函数的图像向左平移 个单位长度，就得到余弦函数的图像，如图.
余弦函数 的图像叫做余弦曲线，它和正弦曲线有相同形状“波浪起伏”的连续光滑曲线.
【1】画出函数的简图：
【2】画出函数的简图：
函数图像的平移和对称变换
【例1】画出函数 的简图.
【解】
取五个关键点列表：
把 的图像向下平移1个单位即可得到 的图像
本资料分享自高中数学同步资源千人教师QQ群483122854 本群专注同步资源收集 期待你的加入与分享
【例2】用五点法分别画出函数 和函数 在 上的图像.
【例3】思考函数 和函数 的关系,并画出函数 的图像.
把函数 图像在 轴下方的部分翻折到 轴上方，加上原来上方的部分就可以得到函数 的图像(蓝色部分)，如图.
【例4】已知函数 （1）作出函数 的图像； (2)求方程 的解.
(1)当 时，
当 时，
所以 ，图像如图所示.
(2)由图像可知方程 的解是