高中人教A版 (2019)5.2.1 三角函数的概念课堂教学ppt课件

这是一份高中人教A版 (2019)5.2.1 三角函数的概念课堂教学ppt课件，共14页。
教材引入&任意角的三角函数定义
【定义】根据研究函数的经验，我们选择在坐标系上研究这个 问题.如图，以单位圆的圆心为原点， 以射线OA为 轴的非负半轴，建立直角坐标系.则A(1，0)，P 射线OA从 轴非负半轴开始，绕点O按逆时针方向 旋转角α，终止位置为OP.
【探究】当 时，点P的坐标是什么？当 或 时，点P的坐标又是什么？给 定一个角α，它的终边OP与单位圆的交点P的坐标是唯一确定的吗？
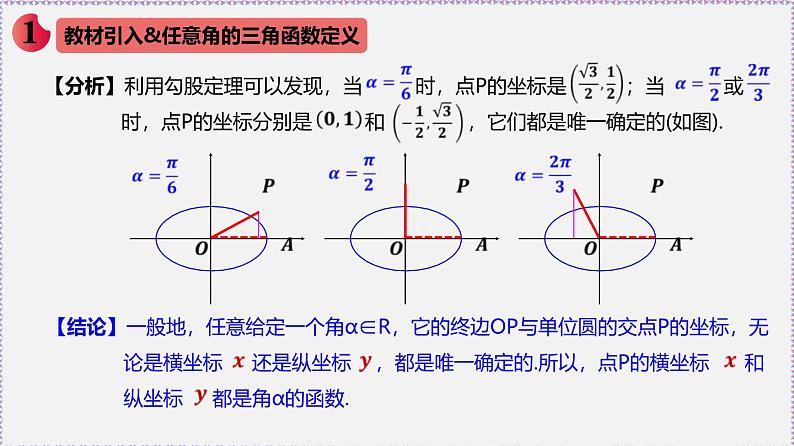
【分析】利用勾股定理可以发现，当 时，点P的坐标是 ；当 或 时，点P的坐标分别是 和 ，它们都是唯一确定的(如图).
【结论】一般地，任意给定一个角α∈R，它的终边OP与单位圆的交点P的坐标，无 论是横坐标 还是纵坐标 ，都是唯一确定的.所以，点P的横坐标 和 纵坐标 都是角α的函数.
【定义】设α是一个任意角，α∈R，它的终边OP与单位圆相交于点P
（1）把点P的纵坐标 叫做α的正弦函数，记作sinα，即 =sinα
（2）把点P的横坐标 叫做α的余弦函数，记作csα，即 =csα
（3）把点P的纵坐标和横坐标的比值 叫做α的正切，记作tanα，即 =tanα ( ).
可以看出，当 时，α的终边始终在y轴上，这时 ，即此时tanα无意义.除此之外，正切tanα与实数α是一一对应的，所以它们之间也是函数关系，我们称 为正切函数.
=tanα ( )
我们把正弦函数、余弦函数和正切函数统称为三角函数.
【总结】三角函数可以看成是以实数α(α为弧度)为自变量，以 单位圆上点的坐标或坐标的比值为函数值的函数.
【注意】（1）在任意角的三角函数定义中，α是一个使函数有意义的实数
（2） 是自变量，离开自变量 的sin,cn,tan是没有意义的
（3）三角函数是比值，是一个实数，这个实数的大小和点P在终边上的 位置无关，终边确定了，三角函数就确定了.
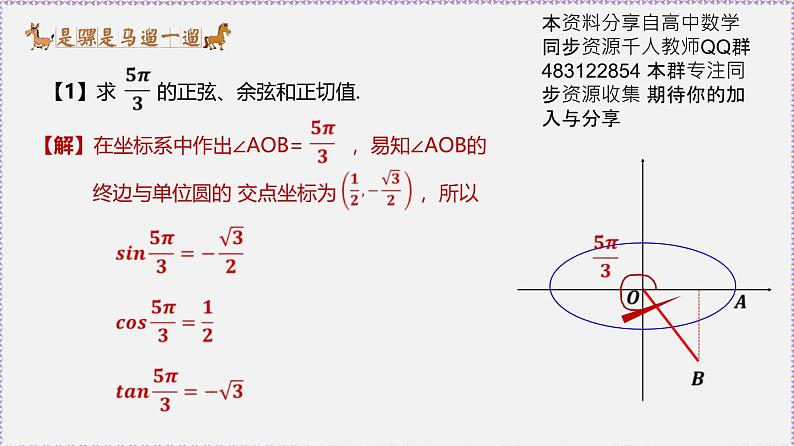
【1】求 的正弦、余弦和正切值.
【解】在坐标系中作出∠AOB= ，易知∠AOB的 终边与单位圆的 交点坐标为 ，所以
本资料分享自高中数学同步资源千人教师QQ群483122854 本群专注同步资源收集 期待你的加入与分享
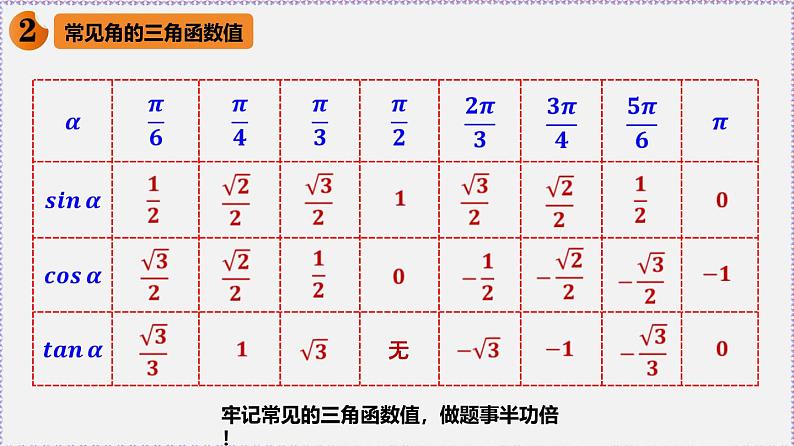
牢记常见的三角函数值，做题事半功倍！
三角函数的定义域和函数值的符号
【1】求证：角θ为第三象限角的充要条件为
【证明】首先证明充分性，即如果①②都成立，那么θ为第三象限角.
因为sinθ＜0成立，所以θ角的终边位于第三或者第四象限，也可能和Y轴的负半轴重合；
又因为csθ＞0成立，所以θ角的终边位于第一或者第三象限，综合可知Θ为第三象限角.
再证明必要性，因为θ是第三象限角，根据定义有sinθ＜0， csθ＞0，所以必要性成立，即充要性成立.
由三角函数的定义，我们知道：终边相同的角的对应三角函数相同.
【问题】公式一说明了角和三角函数值的什么关系？给我们什么启发？
【答】公式一说明了角和三角函数值的对应关系是多角对一值的关系： 即给定一个角，它的三角函数值只要存在，就是唯一的； 反过来，给定一个三角函数值，却有无数个角与之对因.
【启发】做题时，把角同化为(0~2π)即(0°~360°)终边相同的角，简化计算.
【1】已知角α、β的顶点在原点，始边在 轴的正半轴上，终边关于 轴对称， 若角α的终边上有一点的坐标为 ，则tanβ的值是多少？
【解】易知sinα= ，csα= .
因为角α和角β的终边关于y轴对称，则它们的正弦值相等，即sinα=sinβ
同时角α和角β的余弦值相反，即csβ=-csα
β α
所以sinβ= ，csβ= ，所以tanβ=
【3】选择适当的条件填空
①sinθ＞0 ②sinθ＜0 ③csθ＞0④ csθ＜0 ⑤tanθ＞0 ⑥tanθ＜0
(1)角θ为第一象限角的充要条件是 _________________________________
(2)角θ为第一象限角的充要条件是 _________________________________
(3)角θ为第一象限角的充要条件是 _________________________________
(4)角θ为第一象限角的充要条件是 _________________________________
①③或①⑤或③⑤或①③⑤
①④或①⑥或④⑥或①④⑥
②④或②⑤或④⑤或②④⑤
②③或②⑥或③⑥或②③⑥