人教A版 (2019)必修 第一册5.4.2 正弦函数、余弦函数的性质说课课件ppt

这是一份人教A版 (2019)必修 第一册5.4.2 正弦函数、余弦函数的性质说课课件ppt，共17页。PPT课件主要包含了最小正周期为2π，奇函数，偶函数等内容，欢迎下载使用。
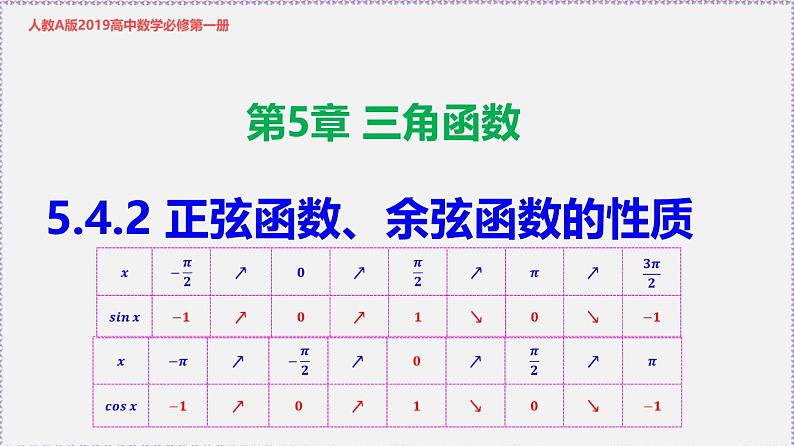
正弦函数、余弦函数的性质
【导学1】一般的函数图像都有哪些性质可以研究？
【解答】图像特点、单调性、奇偶性、最值(极值)等等
【1】周期性：观察正弦函数的图像，可以发现，在图像上，横坐标每隔2π个单位 长度，就会出现纵坐标相同的点，这就是正弦函数值具有的“周而复始”的 变化规律.实际上，这一点既可以从定义中看出，也能从诱导公式中得到反映.即自 变量 的值加上2π的整数倍时所对应的函数值，与 所对应的函数值相等.数学 上用周期性来定量地刻画这种“周而复始”的规律.
【导学2】正弦函数 和余弦函数 的定义域和值域是什么？
【解答】定义域都是R，值域都是[-1，1]
【定义】一般地，设函数 的定义域为D，如果存在一个非零常数T，使得对每一 个 都有 ，且 .那么函数 就叫做 周期函数.非零常数T叫做这个函数的周期.
周期函数的周期不止一个.例如2π，4π，6π以及-2π，-4π，-6π等.都是正弦函数的周期.
如果在周期函数 的所有周期中存在一个最小的正数，那么这个最小正数就叫做 的最小正周期.
根据上述定义，有如下结论：
【1】正弦函数是周期函数，2kπ(k∈Z且k≠0)都是它的的周期，最小正周期是2π
【2】余弦函数是周期函数，2kπ(k∈Z且k≠0)都是它的的周期，最小正周期是2π
①对周期函数与周期定义中的“当 取定义域内的每一个值时”，要特别注意其中 “每一个”的要求.如果只是对某些 有 ，那么T就不是 的周期.
②自变量 本身加的常数才是最小正周期.如 中T不是最小正周 期，因为 ，所以 才是最小正周期.
③周期函数的周期不唯一.若T是函数 的最小正周期，则 也是 函数 的周期.
④并不是所有的周期函数都有最小正周期.例如，对于函数 所有非零实数T都是它的周期，而最小正周期是不存在的，所以常数函数没有最小 正周期.
【例1】求下列函数的周期：
本资料分享自高中数学同步资源千人教师QQ群483122854 本群专注同步资源收集 期待你的加入与分享
【探究】观察正弦曲线和余弦曲线，可以看到正弦曲线关于原点O对称，余弦曲线 关于y轴对称.所以正弦函数是奇函数，余弦函数是偶函数.
【注意】①判断函数的奇偶性时，一定要先判断函数的定义域是否关于原点对称， 只要定义域不关于原点对称，那么这个函数肯定不具备奇偶性.
②由奇偶性我们知道正弦曲线关于原点(0,0)对称，余弦曲线关于y轴(x=0) 对称.
③正弦曲线和余弦曲线即是中心对称图形，又是轴对称图形.
【2】求下列函数的周期
【注意】本题也可以直接用公式求解：
【3】下列函数中，哪些是奇函数？哪些是偶函数？
【探究】由于正弦函数是周期函数，我们可以先在它的一个周期的区间里如 讨论它的单调性，再利用它的周期性，将单调性扩展到整个定义域.
如图可以看到：当 由 增大到 时，曲线逐渐上升， 的值由1减小到-1. 的值变化情况如图所示：
这也就是说，正弦函数 在区间 上单调递增，在区间 上单调递减.
正弦函数在每一个闭区间 上都单调递增，其值从-1增大到1；在每一个闭区间 上都单调递减，其值从1减小到-1.
由上述结果结合正弦函数的周期性我们可以知道：
余弦函数在每一个闭区间 上都单调递增，其值从-1增大到1；在每一个闭区间 上都单调递减，其值从1减小到-1.
同样的道理结合余弦函数的周期性我们可以知道：
【整理】从上述对正弦函数、余弦函数的单调性的讨论中容易得到：
①正弦函数当且仅当 时取得最大值1， 当且仅当 时取得最小值-1；
②余弦函数当且仅当 时取得最大值1， 当且仅当 时取得最小值-1；
【拓展】①正弦、余弦函数图像上最大值处一般称为波峰，最小值处称为波谷.
②正弦函数和余弦函数都不是定义域上的单调函数.
③正弦函数和余弦函数的图像既是轴对称图形也是中心对称图形.
【正弦函数和余弦函数的性质对比】