最新人教版高中数学必修第二册第八章 立体几何 初步章末复习提升课（课件）

这是一份最新人教版高中数学必修第二册第八章 立体几何 初步章末复习提升课（课件），共29页。
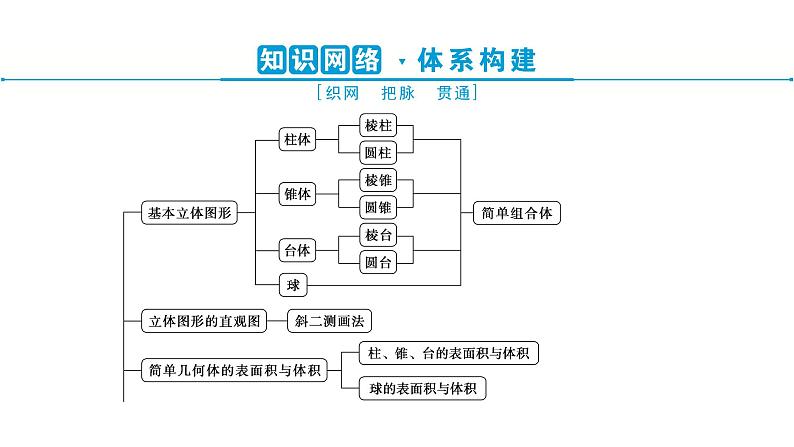
素养一　数学抽象数学抽象让学生养成在日常生活和实践中一般性思考问题的习惯，把握事物的本质，以简驭繁；运用数学抽象的思维方式思考并解决问题．在本章中，主要表现在识别空间几何体结构特征中．
主题1　空间几何体的结构特征 给出下列四种说法：①在圆柱的上、下底面的圆周上各取一点，则这两点的连线是圆柱的母线；②底面为正多边形，且相邻两个侧面与底面垂直的棱柱是正棱柱；③直角三角形绕其任一边所在直线旋转一周所形成的旋转体都是圆锥；④棱台的上、下底面可以不相似，但侧棱长一定相等．其中正确的个数是(　　)A．0B．1C．2D．3
【解析】　①上、下底面的圆周上两点的连线要与轴平行才是母线；③直角三角形绕着直角边所在直线旋转一周才能形成圆锥；④棱台的上、下底面相似，侧棱长不一定相等．故只有②正确．
素养二　数学运算数学运算包括：理解运算对象，掌握运算法则，探究运算思路，选择运算方法，设计运算程序，求得运算结果等．在本章中，主要表现在计算空间几何体的体积、表面积、空间角等问题中．
(2)(2020·高考全国卷Ⅰ)已知A，B，C为球O的球面上的三个点，⊙O1为△ABC的外接圆．若⊙O1的面积为4π，AB＝BC＝AC＝OO1，则球O的表面积为(　　)A．64πB．48πC．36πD．32π
主题3　空间角的计算 如图，正方体的棱长为1，B′C∩BC′＝O，求：(1)AO与A′C′所成的角的大小；(2)AO与平面ABCD所成的角的正切值；(3)平面AOB与平面AOC所成的二面角的大小．
【解】　(1)因为A′C′∥AC，所以AO与A′C′所成的角就是∠OAC.因为AB⊥平面BC′，OC⊂平面BC′，所以OC⊥AB，又OC⊥BO，AB∩BO＝B，所以OC⊥平面ABO.又OA⊂平面ABO，所以OC⊥OA.
即AO与A′C′所成的角为30°.
(2)如图，过点O作OE⊥BC于点E，连接AE.
因为平面BC′⊥平面ABCD，平面BC′∩平面ABCD＝BC，OE⊂平面BC′，所以OE⊥平面ABCD，所以∠OAE为OA与平面ABCD所成的角．
(3)由(1)得OC⊥平面AOB.又OC⊂平面AOC，所以平面AOB⊥平面AOC，即平面AOB与平面AOC所成的二面角为90°.
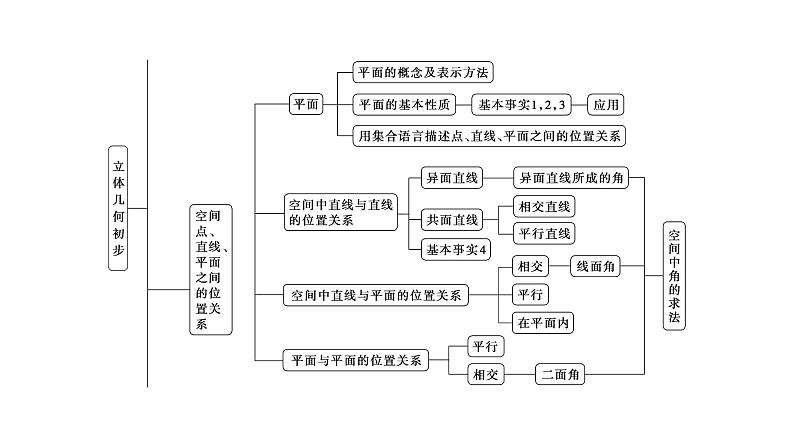
素养三　直观想象直观想象包括：借助空间图形认识事物的位置关系、形态变化与运动规律；利用图形描述、分析数学问题；建立形与数的联系，构建数学问题的直观模型，探索解决问题的思路．在本章中，主要表现在利用几何图形探究线面位置关系中．
主题4　空间中点、线、面的位置关系 (多选)如图所示，在正方体ABCD ­A1B1C1D1中，M，N分别为棱C1D1，C1C的中点，其中正确的是(　　)A．直线AM与C1C是相交直线B．直线AM与BN的平行直线C．直线BN与MB1是异面直线D．直线MN与AC所成的角为60°
【解析】　结合题图，显然直线AM与C1C是异面直线，直线AM与BN是异面直线，直线BN与MB1是异面直线．连接D1C，AD1(图略)，直线MN与AC所成的角即直线D1C与AC所成的角，在等边三角形AD1C中，易知∠ACD1＝60°，所以直线MN与AC所成的角为60°，故选CD.
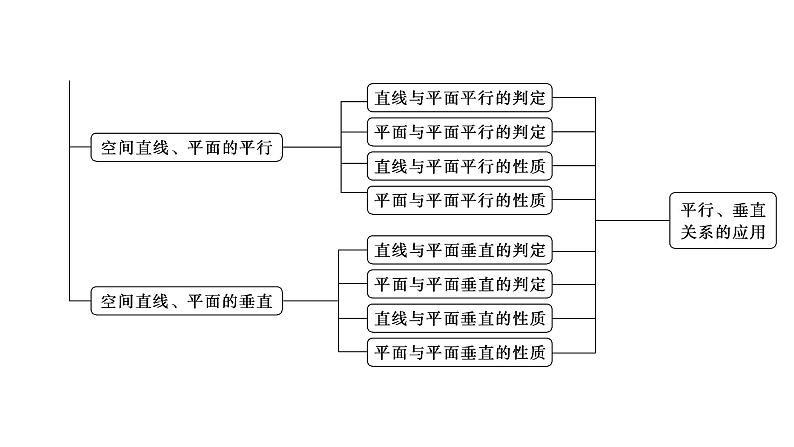
素养四　逻辑推理逻辑推理包括两类：一类是从特殊到一般的推理，推理形式主要有归纳、类比；一类是从一般到特殊的推理，推理形式主要有演绎．在本章中，主要表现在线面位置关系的证明中．
主题5　空间中平行、垂直关系 如图，在四棱锥P­ABCD中，PA⊥平面ABCD，底面ABCD为菱形，E为CD的中点．(1)求证：BD⊥平面PAC；(2)若∠ABC＝60°，求证：平面PAB⊥平面PAE；(3)棱PB上是否存在点F，使得CF∥平面PAE？说明理由．
(1)【证明】　因为PA⊥平面ABCD，BD⊂平面ABCD，所以PA⊥BD.因为底面ABCD为菱形，所以BD⊥AC.又PA∩AC＝A，所以BD⊥平面PAC.
(2)【证明】　因为PA⊥平面ABCD，AE⊂平面ABCD，所以PA⊥AE.因为底面ABCD为菱形，∠ABC＝60°，且E为CD的中点，所以AE⊥CD.所以AB⊥AE.又AB∩PA＝A，所以AE⊥平面PAB.因为AE⊂平面PAE，所以平面PAB⊥平面PAE.
所以FG∥CE，且FG＝CE.所以四边形CEGF为平行四边形．所以CF∥EG.因为CF⊄平面PAE，EG ⊂平面PAE，所以CF∥平面PAE.