安徽省2024八年级数学上学期期中学情评估试卷（附答案沪科版）

这是一份安徽省2024八年级数学上学期期中学情评估试卷（附答案沪科版），共11页。试卷主要包含了选择题，填空题等内容，欢迎下载使用。
1.下列函数：(1)y＝πx；(2)y＝－2x＋1；(3)y＝eq \f(1,x)；(4)y＝2－1－3x；(5)y＝x2－1中，是一次函数的有( )
A．1个 B．2个 C．3个 D．4个
2．若点P(m，1)在第二象限内，则点Q(－m，0)在( )
A．x轴正半轴上 B．x轴负半轴上 C．y轴正半轴上 D．y轴负半轴上
3．在△ABC中，若∠A＝23°，∠B＝46°，则△ABC的形状为( )
A．锐角三角形 B．直角三角形C．钝角三角形 D．等腰三角形
4．下列选项中，可以用来证明命题“若|a－1|＞1，则a＞2”是假命题的反例是( )
A．a＝2 B．a＝1 C．a＝0 D．a＝－1
5．如图，这是围棋棋盘的一部分，将它放置在某个平面直角坐标系中，若白棋②的坐标为(－3，－1)，黑棋①的坐标为(1，－4)，则白棋④的坐标为( )
(第5题)
A．(－2，－3) B．(1，－4) C．(－2，－5) D．(－5，－2)
6．对于直线y＝－eq \f(1,2)x－1的描述，正确的是( )
A．从左至右呈上升趋势 B．不经过第二象限
C．经过点(－2，－2) D．与y轴的交点是(0，－1)
7．若A(x1，y1)，B(x2，y2)是一次函数y＝kx＋b(k>0)图象上两个不相同的点，记p＝(x1－x2)(y1－y2)，则p为( )
A．0 B．正数 C．负数 D．非负数
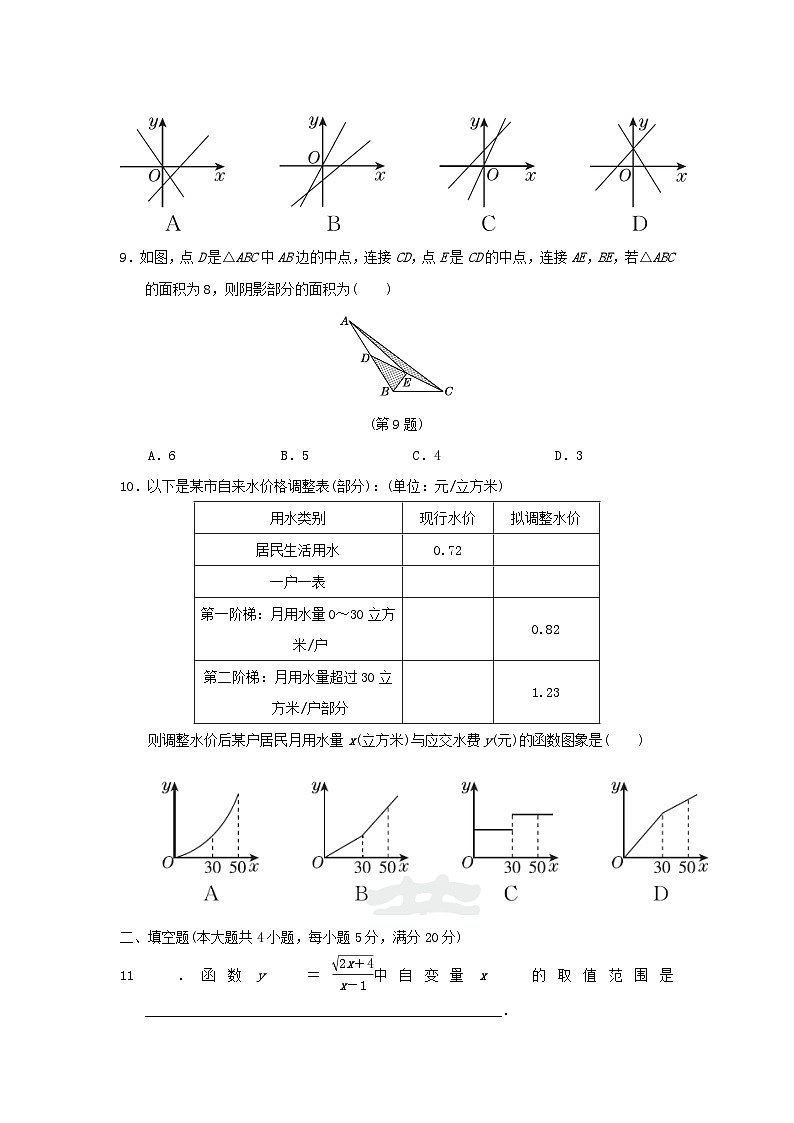
8．在同一坐标系中，函数y＝kx与y＝x－k的大致图象是( )
9．如图，点D是△ABC中AB边的中点，连接CD，点E是CD的中点，连接AE，BE，若△ABC的面积为8，则阴影部分的面积为( )
(第9题)
A．6B．5C．4D．3
10．以下是某市自来水价格调整表(部分)：(单位：元/立方米)
则调整水价后某户居民月用水量x(立方米)与应交水费y(元)的函数图象是( )
二、填空题(本大题共4小题，每小题5分，满分20分)
11．函数y＝eq \f(\r(2x＋4),x－1)中自变量x的取值范围是___________________________________________________．
12．“相等的两个角不互补”它是________命题(填“真”或“假”)，改写成“ 如果……那么……”的形式为______________________________________．
13．在△ABC中，∠A＝90°，BD，CE是△ABC的角平分线且相交于点O，则∠BOC的度数为________．
14．在平面直角坐标系中，已知一次函数的图象经过A(－2，4)，B(1，1)．
(1)该一次函数的表达式为____________；
(2)若直线y＝kx(k≠0)与线段AB有公共点，则k的取值范围为________________．
三、(本大题共2小题，每小题8分，满分16分)
15．在△ABC中，AB＝7，BC＝2.
(1)求AC长度的取值范围；
(2)若△ABC的周长为偶数，求△ABC的周长，并判断此时△ABC的形状．
16．已知y与x＋2成正比例，当x＝4时，y＝12.
(1)求y与x之间的函数表达式；
(2)判断点(－1，1)是否在所求函数的图象上，并说明理由．
四、(本大题共2小题，每小题8分，满分16分)
17．如图，在平面直角坐标系中，已知A(－2，2)，B(2，0)，C(3，3)，P(m，n)是△ABC的边AB上的一点，把△ABC经过平移后得到△DEF，点A，B，C的对应点分别为点D，E，F，点P的对应点为P1(m－2，n－4)．
(1)直接写出D，E，F三个点的坐标并画出△DEF；
(2)求△DEF的面积．
(第17题)
18．如图，已知函数y＝2x＋b和y＝ax－3的图象交于点P(－2，－5)，这两个函数的图象与x轴分别交于点A，B.
(1)分别求出这两个函数的表达式；
(2)求△ABP的面积；
(3)根据图象直接写出不等式2x＋b>ax－3的解集．
(第18题)
五、(本大题共2小题，每小题10分，满分20分)
19．(1) 完成下面的推理说明：
已知： 如图，BE∥CF，BE，CF分别平分∠ABC和∠BCD.
求证：AB∥CD.
证明：∵BE，CF分别平分∠ABC和∠BCD(已知)，
∴∠1＝eq \f(1,2)∠______，∠2＝eq \f(1,2)∠______(____________)．
(第19题)
∵BE∥CF(____________)，
∴∠1＝∠2(______________________)．
∴eq \f(1,2)∠______＝eq \f(1,2)∠______(____________)，
∴∠______＝∠______(等式的基本性质)，
∴AB∥CD(______________________)．
(2) 说出 (1) 的推理中运用了哪两个互逆的真命题．
20．一种斜挎包，其挎带由双层部分、单层部分和调节扣构成．通过调节扣加长或缩短单层部分的长度，可以使挎带的长度加长或缩短(挎带的长度是单层部分与双层部分长度的和，其中调节扣所占的长度忽略不计)．设单层部分的长度为x cm，双层部分的长度为y cm，经测量，得到如下数据：
(1)根据表中数据的规律，完成以上表格，并直接写出y关于x的函数表达式；
(2)当挎带的长度为100 cm时，请求出此时单层部分的长度；
(3)设挎带的长度为a cm，求a的取值范围．
六、(本题满分12分)
21．小明和小华家在同一小区，周末两人从小区同时出发去广场．已知小华匀速步行前往，小明先以150 m/min的速度骑自行车前往，中间休息了20 min后再重新以另一速度骑行到达广场．如图是两人与小区的距离y(m)关于出发时间x(min)之间的函数图象．
(1)a＝________，b＝________；
(2)求小明和小华第二次相遇时，两人与广场之间的距离；
(3)小明重新出发后，再骑行多长时间与小华相距300 m?
(第21题)
七、(本题满分12分)
22．已知：在△ABC中，BO平分∠ABC，BO，CO相交于点O.
(1)如图①，若CO⊥BC，∠BOC＝50°，∠ACB＝42°，则∠A＝________________________________________________________.
(2)如图②，若CO平分∠ACB，且∠BOC＝3∠A，则∠A＝________________________________________.
(3)如图③，若CO在△ABC的外角∠ACM内，且∠ACO∶∠OCM＝1∶3，∠BOC＝eq \f(4,5)∠A，试探究：∠A与∠ABC的数量关系．
(第22题)
八、(本题满分14分)
23．某地某公司提供的流量套餐有三种，如表所示．
x表示每月上网流量(单位：GB)，y表示每月的流量费用(单位：元)，三种套餐对应的y关于x的关系如图所示．
(1)当x>5时，求A套餐每月的流量费用yA关于每月上网流量x的函数表达式．
(2)当每月上网流量在什么范围时，选择C套餐最为划算？
(3)小红爸妈各选一种套餐，计划2人每月流量总费用控制在150元以内(包括150元)，请为他们设计一种方案使总流量达到最大(填如下表格即可)．
(第23题)
答案
一、1.C 2.A 3.C 4.D 5.C 6.D 7.B 8.B 9.C
10．B
二、11.x≥－2且x≠1
12．假；如果两个角相等，那么这两个角不互补 13.135°
14．(1)y＝－x＋2 (2)k≥1或k≤－2
三、15.解：(1)∵AB＝7，BC＝2，∴7－2