浙江省绍兴市绍初教育集团2024-2025学年九年级上学期10月月考数学试题

这是一份浙江省绍兴市绍初教育集团2024-2025学年九年级上学期10月月考数学试题，共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题：本大题有10个小题，每小题3分，共30分．
1．下列事件中，是必然事件的是（ ）
A．经过有交通信号灯的路口，遇到红灯 B．射击运动员射击一次，命中靶心
C．购买一张彩票，中奖 D．任意画一个三角形，其内角和是180°
2．下列四个点中，在抛物线上的点是（ ）
A．（2，1） B．（2，-1） C．（1，2） D．（1，-2）
3．对于二次函数的性质，下列描述正确的是（ ）
A．开口向下 B．对称轴是直线
C．当时，y随x的增大而增大 D．顶点坐标是（2，1）
4．下列函数中，当时，y随x增大而增大的是（ ）
A． B． C． D．
5．如图，以40m/s的速度将小球沿与地面成30°角的方向击出时，小球的飞行路线将是一条抛物线．如果不考虑空气阻力，小球的飞行高度h（单位：m）与飞行时间t（单位：s）之间具有函数关系，下列对方程的两根与的解释正确的是（ ）
A．小球的飞行高度为15m时，小球飞行的时间是1s
B．小球从飞出到落地要用4s
C．小球飞行3s时飞行高度为15m，并将继续上升
D．小球的飞行高度可以达到25m
6．二次函数，（，a，b，c为常数）的部分对应值列表如下：
则代数式的值为（ ）
A．1 B．2 C．3 D．4
7．抛掷一枚质地均匀的硬币，若抛掷8次都是正面朝上，则抛掷第9次（ ）
A．正面朝上的可能性大 B．反面朝上的可能性大
C．无法确定 D．正面朝上与反面朝上的可能性一样大
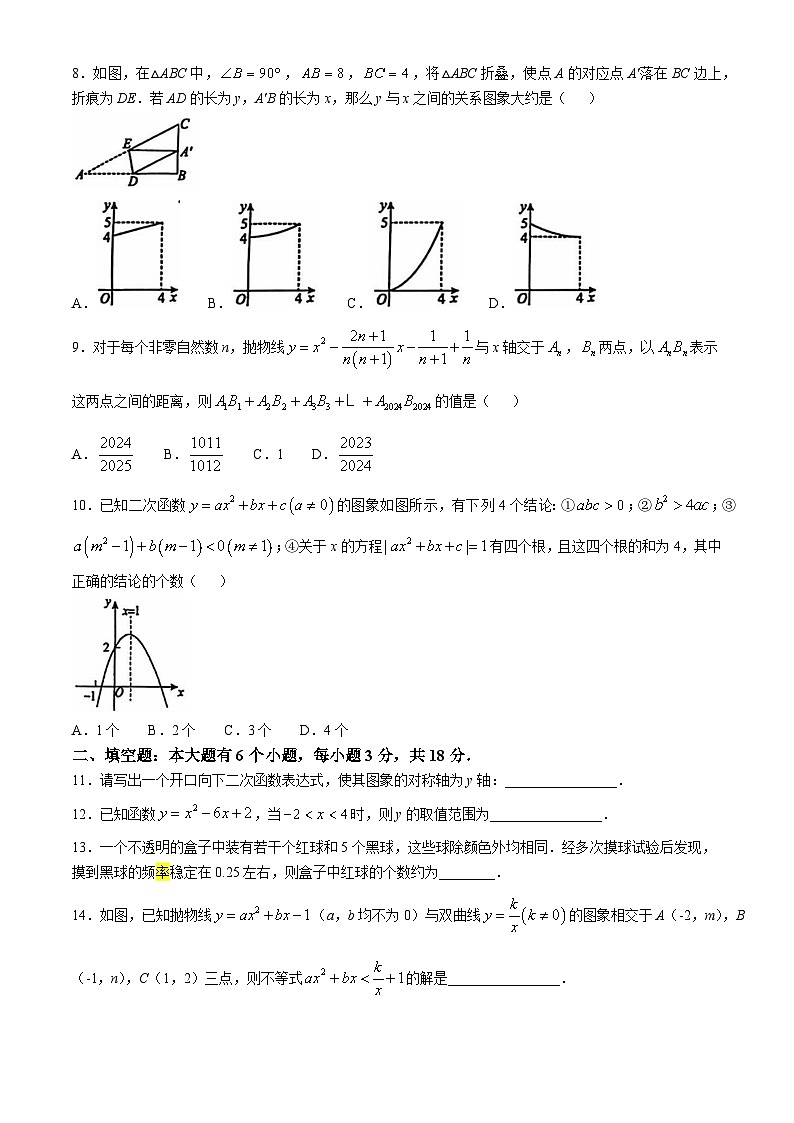
8．如图，在△ABC中，，，，将△ABC折叠，使点A的对应点A′落在BC边上，折痕为DE．若AD的长为y，A′B的长为x，那么y与x之间的关系图象大约是（ ）
A． B． C． D．
9．对于每个非零自然数n，抛物线与x轴交于，两点，以表示这两点之间的距离，则的值是（ ）
A． B． C．1 D．
10．已知二次函数的图象如图所示，有下列4个结论：①；②；③；④关于x的方程有四个根，且这四个根的和为4，其中正确的结论的个数（ ）
A．1个 B．2个 C．3个 D．4个
二、填空题：本大题有6个小题，每小题3分，共18分．
11．请写出一个开口向下二次函数表达式，使其图象的对称轴为y轴：________________．
12．已知函数，当时，则y的取值范围为________________．
13．一个不透明的盒子中装有若干个红球和5个黑球，这些球除颜色外均相同．经多次摸球试验后发现，摸到黑球的频率稳定在0.25左右，则盒子中红球的个数约为________．
14．如图，已知抛物线（a，b均不为0）与双曲线的图象相交于A（-2，m），B（-1，n），C（1，2）三点，则不等式的解是________________．
15．已知函数的图象与坐标轴只有两个交点，则m＝________．
16．已知点A是直线上一动点，以点A为顶点的抛物线交y轴于点B，作点B关于x轴的对称点C，连接AB、AC．若△ABC是直角三角形，则点A的坐标为________________．
三、解答题：本大题有8个小题，共72分．
17．（6分）根据下列条件求a的取值范围：
（1）函数，当时，y随x的增大而减小，当时，y随x的增大而增大；
（2）函数有最大值；
（3）函数的图象是开口向上的抛物线．
18．（6分）已知二次函数，过（1，-32），在时取到最大值，且二次函数的图象与直线交于点P（m，0）．
（1）求这个二次函数解析式；
（2）求大于时，x的取值范围．
19．（8分）高尔基说：“书，是人类进步的阶梯．”阅读可以启智增慧，拓展视野．为了解学生寒假阅读情况，开学初学校进行了问卷调查，并对部分学生假期（28天）的阅读总时间作了随机抽样分析，设被抽样的每位同学寒假阅读的总时间为t（小时），阅读总时间分为四个类别：A（），B（），C（），D（），将分类结果制成两幅统计图（尚不完整）．根据以上信息，回答下列问题：
（1）请补全条形统计图；
（2）扇形统计图中a的值为________；
（3）若该校有2000名学生，估计寒假阅读总时间少于24小时的学生有多少名？
（4）政教处决定从本次调查阅读时长前四名学生甲、乙、丙、丁中，随机抽取2名同学参加该校“阅读之星”竞选，请用树状图或列表法求恰好选中甲和乙的概率．
20．（8分）已知抛物线与x轴交于点A（1，0），B（3，0），且过点C（0，-3）．
（1）求指物线的解析式和顶点坐标；
（2）请写出两种一次平移的方法，使平移后抛物线的顶点落在直线上，并写出平移后相应的抛物线解析式．
21．（10分）为实施“乡村振兴”计划，某村产业合作社种植了“千亩桃园”．2024年该村桃子丰收，销售前对本地市场进行调查发现：当批发价为4千元/吨时，每天可售出12吨，每吨涨1千元，每天销量将减少2吨，据测算，每吨平均投入成本2千元，为了抢占市场，薄利多销，该村产业合作社决定，批发价每吨不低于4千元，不高于5.5千元．请解答以下问题：
（1）求每天销量y（吨）与批发价x（千元/吨）之间的函数关系式，并直接写出自变量x的取值范围；
（2）当批发价定为多少时，每天所获利润最大？最大利润是多少？
22．（10分）科研人员为了研究弹射器的某项性能，利用无人机测量小钢球竖直向上运动的相关数据．无人机上升到离地面30米处开始保持匀速竖直上升，此时，在地面用弹射器（高度不计）竖直向上弹射一个小钢球（忽略空气阻力），在1秒时，它们距离地面都是35米，在6秒时，它们距离地面的高度也相同．其中无人机离地面高度（米）与小钢球运动时间x（秒）之间的函数关系如图所示；小钢球离地面高度（米）与它的运动时间x（秒）之间的函数关系如图中抛物线所示．
（1）直接写出与x之间的函数关系式；
（2）求出与x之间的函数关系式；
（3）小钢球弹射1秒后直至落地时，小钢球和无人机的高度差最大是多少米？
23．（12分）如图，已知直线与x轴交于点A，与y轴交于点C，抛物线经过A，C两点，且与x轴的另一个交点为B，对称轴为直线．
（1）求抛物线的表达式；
（2）D是第二象限内抛物线上的动点，设点D的横坐标为m，求四边形ABCD面积S的最大值及此时D点的坐标；
（3）若点P在抛物线对称轴上，是否存在点P，Q，使以点A，C，P，Q为顶点的四边形是以AC为对角线的菱形？若存在，请求出P，Q两点的坐标；若不存在，请说明理由．
24．（12分）已知二次函数．
（1）当时，
①若该函数图像的对称轴为直线，且过点（0，3），求该函数的表达式；
②若方程有两个相等的实数根，求证：；
（2）若，已知点，点，当二次函数的图像与线段MN有交点时，求出a的取值范围．
绍初教育集团十月份教学调测卷参考答案
一、选择题：本大题有10个小题，每小题3分，共30分．
二、填空题：本大题有6个小题，每小题3分，共18分．
11．答案不唯一 12． 13．15 14．或
15．0或-2或 16．或或
三、解答题：本大题有8个小题，共72分．17题6分，18题6分，19题8分，20题8分，21题10分，22题10分，23题12分，24题12分．
17．（1）； （2）； （3）
18．解：（1）将（m，0）代入得，
解得．∴P（-1，0）
由题意可得抛物线对称轴为直线，
∴，，
把（1，-32），（-1，0）代入得，
解得，
∴．或者设顶点式得
（2）令，解得或，
∴抛物线与直线交点横纵标为-1和，
如图，
∴时，大于．
19．（1）解：本次抽样的学生人数为：（人），
∴C组的人数为：（人），
补全条形统计图如下：
（2）解：A组所占的百分比为：，
∴，
（3）解：（名）．
答：估计寒假阅读的总时间少于24小时的学生有1000名．
（4）解：画树状图如下：
共有12种等可能的结果，其中恰好选中甲和乙的结果有2种．
∴恰好选中甲和乙的概率为．
20．解：（1）∵抛物线与x轴交于点A（1，0），B（3，0），可设抛物线解析式为，
把C（0，-3）代入得：，
解得：，
故抛物线解析式为，
即，
∵，
∴顶点坐标（2，1）；
（2）平移方法有：
①向下平移5个单位，得到：，
把代入得出，
∵顶点坐标（2，1）；
∴向下平移5个单位，抛物线的顶点为（2，-4）；
②向左平移2.5个单位，得到：，
把代入得出，
∴向左平移2.5个单位，抛物线的顶点为．
21．（1）解：根据题意得，
所以每天销量y（吨）与批发价x（千元/吨）之间的函数关系式，自变量x的取值范围是
（2）解：设每天获得的利润为w千元，根据题意得
，
∵，
∴当，w随x的增大而增大．
∵，
∴当时，w有最大值，最大值为，
∴将批发价定为每吨5.5千元时，每天获得的利润最大，最大利润是31.5千元．
22．解：（1）设与x之间的函数关系式为，
∵函数图象过点（0，30）和（1，35），
则，解得，
∴与x之间的函数关系式为．
（2）∵时，，
∵的图象是过原点的抛物线，
∴设，
∴点（1，35），（6，60）在抛物线上．
∴，即，解得，
∴．
（3）设小钢球和无人机的高度差为y米，
由得或．
①时，
，
∵，∴抛物线开口向下，
又∵1＜x≤6，
∴当时，y的最大值为；
②时，
，
∵，∴抛物线开口向上，
又∵对称轴是直线，
∴当时，y随x的增大而增大，
∵，
∴当时，y的最大值为70．
∵，∴高度差的最大值为70米．
23．解：（1）对于，当时，，当时，，
∴点A的坐标为（-3，0），点C的坐标为（0，4），
∵对称轴是直线：，
∴有：，解得：，
∴抛物线的表达式为：；
（2）对于，当时，，解得：，，
∴点B的坐标为（0，1），
又∵点A（-3，0），点C（0，4），∴，，
作轴于E，
∵点D在第二象限内的抛物线上，且横坐标为m
∴点D的坐标为（m，n），则，
∴，，
∴，
∵轴，则四边形OCDE为直角梯形，
∴，
又，，
∴，
即，
又，
，
当时，S为最大，
此时
∴点D的坐标为（-1.5，5）．
（3）存在点P和点Q，使以点A，C，P，Q为顶点的四边形是以AC为对角线的菱形，
理由如下：
∵点P在抛物线的对称轴上，
∴可设点P的坐标为：（-1，t），
∵以A，C，P，Q为顶点的四边形是以AC为对角线的菱形，
∴，AC与PQ互相垂直平分，
设直线与x轴交于点F，过点P作轴，AC与PQ交于点K，
∵点A（-3，0），C（0，4），
∴，，，，
∴，，
在Rt△APF中，由勾股定理得：，
在Rt△CPT中，由勾股定理得：
∴，解得：，
∴点P的坐标为，
设点K的坐标为，
∵点K为AC的中点，∴，，
设点Q的坐标为，
∵点K为PQ的中点，∴，，
解得：，，∴点Q的坐标为．
24．（1）解：①∵，对称轴为直线，
∴
∴，
把点（0，3）代入得，，
∴该函数的表达式为；
②∵方程有两个相等的实数根，
∴，
∴，
∴，
∵，∴，
∴；
（2）解：∵，∴，，
∴，
∴抛物线的顶点为（2，-a），
把代入得，，
解得或，
∴抛物线与x轴的交点为（1，0）、（3，0），
当抛物线过点时，，
解得，
如图，根据|a|越大，抛物线的开口越小，当时，二次函数的图像与线段MN有交点，
当抛物线过点时，，
解得，
如图，当时，二次函数的图像与线段MN有交点，
综上所述，当或时，二次函数的图像与线段MN有交点．
x
…
-2
-1
0
1
…
y
…
-2
-3
-2
1
…
题号
1
2
3
4
5
6
7
8
9
10
答案
D
C
C
A
B
A
D
B
A
C