六安市毛坦厂中学实验学校2024届九年级上学期第一次月考数学试卷(含答案)

这是一份六安市毛坦厂中学实验学校2024届九年级上学期第一次月考数学试卷(含答案)，共6页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
九年级数学模拟试卷
学校:___________姓名：___________班级：___________考号：___________
一、单选题
1．下列函数中，属于二次函数的是（ ）
A．B．C．D．
2．抛物线的顶点坐标是（ ）
A．B．C．D．
3．如图，已知点P是双曲线上任意一点，过点P作PA⊥y轴于点A，B是x轴上一点，连接AB、PB，若△PAB的面积为2，则双曲线的解析式为（ ）
A．yB．yC．yD．y
（3）（5）
4．在同一坐标系内，函数y＝kx2和y＝kx﹣2（k≠0）的图象大致如图（ ）
A． B．
C．D．
5．抛物线的图象如图所示，对称轴为直线，与y轴交于点，则下列结论中正确的是（ ）
A．B．
C．D．当时，y随x的增大而减小
6．某超市销售一种商品，每件成本为元，销售人员经调查发现，该商品每月的销售量（件）与销售单价（元）之间满足函数关系式，若要求销售单价不得低于成本，为每月所获利润最大，该商品销售单价应定为多少元？每月最大利润是多少？（ ）
A．元，元B．元，元
C．元，元D．元，元
7．已知点，，都在二次函数的图象上，那么、、的大小关系是（ ）
A．B．C．D．
8．二次函数的图象过点，方程的解为（ ）
A．B．
C．D．
9．如图，在平面直角坐标系中，点A、E在抛物线上，过点A、E分别作y轴的垂线，交抛物线于点B、F，分别过点E、F作x轴的垂线交线段AB于两点C、D．当点，四边形为正方形时，则线段的长为（ ）
A．4B． C．5D．
10．如图，正方形边长为4，E、F、G、H分别是上的点，且．设A、E两点间的距离为x，四边形的面积为y，则y与x的函数图象可能是（ ）

A． B．C． D．
二、填空题
11．将二次函数的图象向右平移1个单位长度，再向上平移2个单位长度，平移后的二次函数的图象的顶点坐标是 ．
12．为执行国家药品降价政策，给人民群众带来实惠，某药品经过两次降价，每盒零售价由元降为元，设平均每次降价的百分率是，则关于的函数表达式为 ．
13．如图，正比例函数y=kx与反比例函数y=的图象有一个交点A(2，m)，AB⊥x轴于点B，平移直线y=kx使其经过点B，得到直线l，则直线l对应的函数表达式是 .
14．在平面直角坐标系中，设二次函数，其中．
（1）此二次函数的对称轴为直线 ；
（2）已知点和在此函数的图象上，若，则的取值范围是 ；
三、解答题
15．已知二次函数与x轴的交点（-1，0）和（3，0），求其函数解析式并通过配方法求出函数的最大值．
16．已知抛物线与x轴交于A、B两点．
(1)求该抛物线的对称轴；
(2)求线段AB的长．
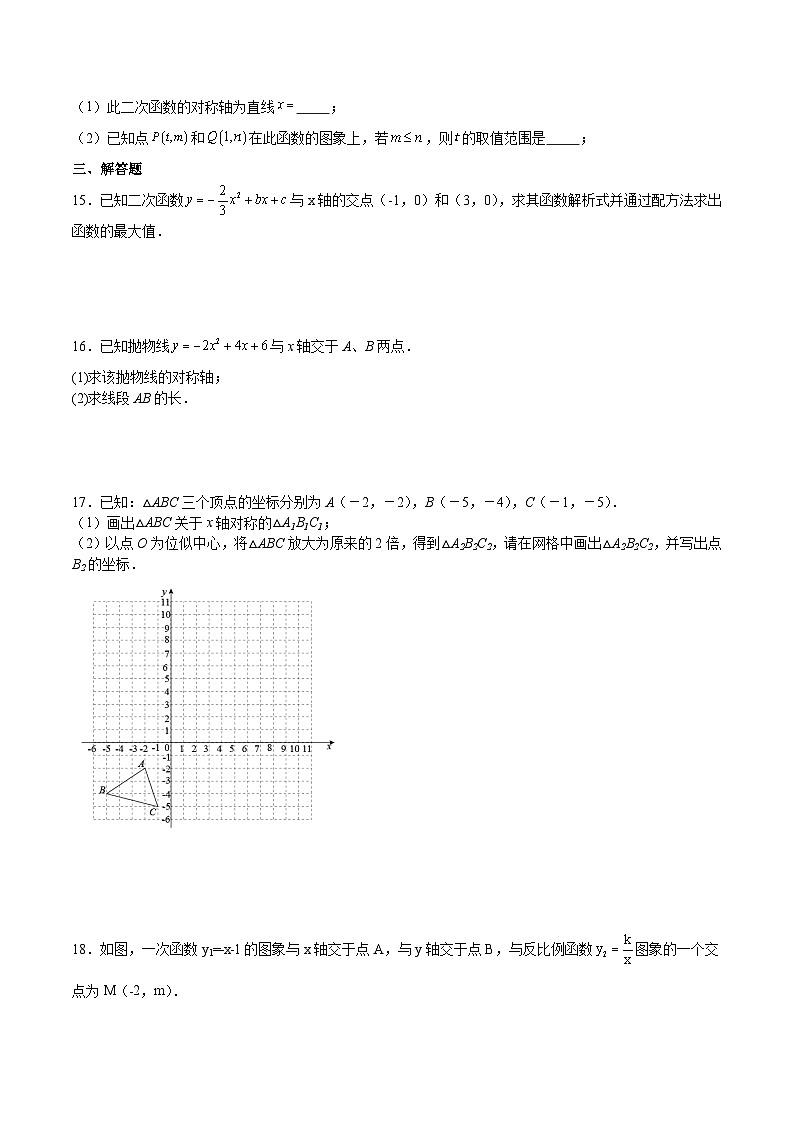
17．已知：△ABC三个顶点的坐标分别为A（－2，－2），B（－5，－4），C（－1，－5）．
（1）画出△ABC关于x轴对称的△A1B1C1；
（2）以点O为位似中心，将△ABC放大为原来的2倍，得到△A2B2C2，请在网格中画出△A2B2C2，并写出点B2的坐标．
18．如图，一次函数y1=﹣x﹣1的图象与x轴交于点A，与y轴交于点B，与反比例函数图象的一个交点为M（﹣2，m）．
（1）求反比例函数的解析式；
（2）求点B到直线OM的距离．
19．某公司分别在A、B两城生产一批同种产品共100件，A城生产产品的成本y（万元）与产品数量x（件）之间的函数关系为，当时，；当时，．B城生产产品的每件成本为70万元．
(1)求A城生产产品的成本y（万元）与产品数量x（件）之间的函数关系式；
(2)当A、B两城生产这批产品的总成本的和最少时，求A、B两城各生产多少件．
20．若一个函数的解析式等于另两个函数解析式的和，则这个函数称为另两个函数的“生成函数”．现有关于x的两个二次函数，且， 的“生成函数”为：；当时，；二次函数的图像的顶点坐标为．
(1)求m的值；
(2)求二次函数的解析式．
21．如图，西游乐园景区内有一块矩形油菜花田地（单位：），现在其中修建一条观花道（阴影所示），供游人赏花，设改造后观花道的面积为．
(1)求与的函数关系式；
(2)若改造后观花道的面积为，求的值；
(3)若要求，求改造后油菜花地所占面积的最大值．
22．在平面直角坐标系中，抛物线的顶点为，与轴相交于点．
(1)点的坐标为________，点的坐标为________；（用含的式子表示）
(2)设抛物线的函数图象最高点的纵坐标为．
①当时，________；当时，________；
②写出关于的函数解析式及自变量的取值范围．
23．小明在一次打篮球时，篮球传出后的运动路线为如图所示的抛物线，以小明所站立的位置为原点O建立平面直角坐标系，篮球出手时在O点正上方1m处的点P.已知篮球运动时的高度y(m)与水平距离x(m)之间满足函数表达式y=-x2+x+c.
（1）求y与x之间的函数表达式；
（2）球在运动的过程中离地面的最大高度；
（3）小亮手举过头顶，跳起后的最大高度为BC=2.5m，若小亮要在篮球下落过程中接到球，求小亮离小明的最短距离OB．
参考答案：
1．C
2．B
3．C
4．B
5．C
6．B
7．D
8．B
9．B
10．A
11． 12． 13．y=x-3
14． /0.5
15．，，最大值是
16．(1)直线；(2)
17．（1）12；（2）B2(10，8) ．
18．（1）（2）．
19．(1)
(2)当A，B两城生产这批产品的总成本的和最少时，A，B两城分别生产20件、80件
20．(1);(2)
21．(1)(2)(3)
22．(1)，
(2)①1，；②
23．(1)y与x的函数表达式为y=-x2+x+1；(2)篮球在运动的过程中离地面的最大高度为3m；(3)小亮离小明的最短距离为6m.